深入浅出图神经网络 第6章 GCN的性质 读书笔记

第6章 GCN的性质

第5章最后讲到GCN结束的有些匆忙，作为GNN最经典的模型，其有很多性质需要我们去理解。

6.1 GCN与CNN的区别与联系

CNN卷积卷的是矩阵某个区域内的值，图卷积在空域视角下卷的是节点的邻居的值，由此粗略来看二者都是在聚合邻域的信息。

再具体来看一些区别与联系：

图像是一种特殊的图数据

图数据经常是非结构化的，能够表达数据间更复杂的关系。考虑对图像进行卷积时卷的是某一像素周围\(3\times3\)的像素，将中间的像素看作节点，那么周围的像素就是其邻居，相当于CNN在对其周围结构非常规则的邻居在做卷积。对于GCN则是图结构是什么样的图卷积就在卷哪些邻居，所以GCN能更好处理非结构化的数据。

从网络连接方式来看，二者都是局部连接

对单个节点来说GCN卷的是其一阶的邻居，CNN卷的是其附近\(n\times n\)的值。这种节点下一层的特征计算只依赖于自身邻域的方式，在网络连接上表现为一种局部连接的结构。

但就权重设置上来看，CNN的卷积核一般有多组权重参数，而GCN为了适应不同的图数据结构只有一组，所以CNN的拟合能力实际上强于GCN。

二者卷积核的权重是处处共享的

CNN和GCN卷积核的权重都是用于全图的，这样减少了网络的参数量，可以避免过拟合的出现。

从模型的层面来看，感受域随着卷积层的增加而变大

CNN和GCN一样每多卷一层感受域都会变得更大，这也比较好理解。假设CNN卷积核\(n\times n\)，那一个节点卷一次就变成了\(n\times n\)，再卷一次就变成了\((2n-1)\times(2n-1)\)...对于GCN也是，卷一次是一阶邻居，两次就是二阶段邻居了。

GCN能够对图数据进行端到端学习

感觉这个小标题就足以说明GCN的性质了...

回顾一下之前我们在Cora数据集上进行的GCN实战，我们的输入就是引文网络的图结构，输出的就是节点的分类，这正是端到端学习的定义。也就是说GCN不需要我们人工地提取一些节点特征作为输入来辅助网络进行学习。

对于一个图数据，我们需要关注的是其结构信息和属性信息，结构信息就是图的结构，属性信息就是节点的特征，二者都应该被学习到。由此书中列举了手工提取特征和随机游走两种非端到端的学习的例子，看一下就好，其共同点就是都需要将结构信息和节点特征拼接起来作为新的节点信息。

GCN能够对图数据进行端到端学习有两种优势：

1. GCN不会分开进行表示学习和任务学习，也就是GCN在对图数据进行建模提取特征的同时也在从特征进行任务学习，结合前面说到的GCN的权重是处处共享的，这让整个模型在同步地更新使得节点的特征表示与下游任务之间具有更好的适应性
2. GCN对结构信息与属性信息的学习是同时进行的

GCN是一个低通滤波器

在图的半监督学习中，通常会在损失函数里增加一个正则项，用来保证相邻节点之间的类别信息趋于一致，一般会选用拉普拉斯矩阵的二次型作为正则约束：

\[L=L_0+L_{reg} \\L_{reg}=\sum_{e_{ij}\in E} A_{ij}||f(x_i)-f(x_j)||^2=f(X)^TLf(X) \]

回顾第5章中讲到的总变差，我们可以注意到加入的正则项实际上就是图信号的总变差，将其加入损失函数后，减小总变差说明图信号更加平滑，从而说明相邻节点之间的信号更加趋于一致，即类别信息趋于一致。从频域上来看，这样做就相当于对图信号进行了一次低通滤波。

但是对于GCN的损失函数（通常是用交叉熵）并不会加入这样一个正则项，因为GCN本身就可以看做是一个低通滤波器。

回顾GCN的核心计算\(\tilde L_{sym}XW\)，我们说过\(\tilde L_{sym}X\)可以看做是一次图滤波操作，那么我们来考虑\(\tilde L_{sym}\)的频率响应函数\(h()\)（明明上一章还用的\(h()\)，结果这章书里写的就是\(p()\)了，有点迷惑，所以我沿用\(h()\)的写法）。

\[\tilde L_{sym}=\tilde D^{-\frac{1}{2}}\tilde A\tilde D^{-\frac{1}{2}}=\tilde D^{-\frac{1}{2}}(\tilde D-L)\tilde D^{-\frac{1}{2}}=I-\tilde D^{-\frac{1}{2}}L\tilde D^{-\frac{1}{2}}=I-\tilde L_s \]

可以证明\(\tilde L_s\)可以被正交对角化，所以设\(\tilde L_s=V\tilde\Lambda V^T\)，\(\tilde\lambda_i\)是特征值，同样可以证明特征值属于\((0,2]\)。

所以可以继续将等式变换为：

\[\tilde L_{sym}=I-V\tilde\Lambda V^T=V(1-\tilde\Lambda)V^T \]

所以其频率响应函数为\(h(\lambda)=1-\tilde \lambda_i \in [-1,1)\)。说明函数能够起到显性收缩的作用，因而能对图信号进行低通滤波。

如果多次左乘\(\tilde L_{sym}\)可以有如下频率响应函数的图像：

注意到在低频上K越大缩放效果越强，对应的就是更强的低通滤波器。

那么GCN是低通滤波器对图数据的学习有什么好处呢？一篇paper分析了这个问题，比较硬核所以只给出结论：低频信号通常包含着对任务学习更加有效的信息。

GCN的问题——过度平滑

过度平滑简单来说就是多层GCN叠加之后反而会出现准确率下降的问题。我们从频域和空域两个角度来看这一问题。

频域视角

前面分析过了GCN对应的频率响应函数是\(h(\lambda)=1-\tilde\lambda_i\)，多层GCN就是\((1-\tilde\lambda_i)^k\)，因为\(1-\tilde \lambda_i \in [-1,1)\)，假设图是全连通图，仅存在一个特征值为0，那么也就只有一个\(1-\tilde \lambda_i=1\)，所以取极限后对应的\(H\)只有一个值为1，剩下的全为0，即：

\[\lim_{k\to+\infin}\tilde L_{sym}^k=V \begin{bmatrix} 1\\ &0\\ &&\ddots\\ &&&0 \end{bmatrix}V^T \]

那么有：

\[\lim_{k\to+\infin}\tilde L_{sym}^kx=V \begin{bmatrix} 1\\ &0\\ &&\ddots\\ &&&0 \end{bmatrix}V^Tx=\tilde x_1v_1 \]

\(v_1\)是特征值为0对应的特征向量，\(\tilde x_1\)是x在特征值为0这一频率对应的傅里叶系数。

可以证明\(v_1=\tilde D^{\frac{1}{2}}1\)（用到拉普拉斯矩阵存在全为1的特征向量，对应特征值为0），这里1表示全为1的向量。这是一个固定的向量，说明如果不断地进行GCN层的计算，最后图信号实际上会处处相等，也就是学不到东西了。

空域视角

空域视角比较直观，一层GCN是聚合了一层邻居节点的信息，那两层就是两跳邻居的信息...最后足够多层的GCN就会聚合全图的信息，并且对每个节点来说学习的都是全图的信息，导致节点之间没有区分性。

解决GCN的过度平滑问题也是研究的热点，书中举了JK-Net的例子，其主要的解决方法是：

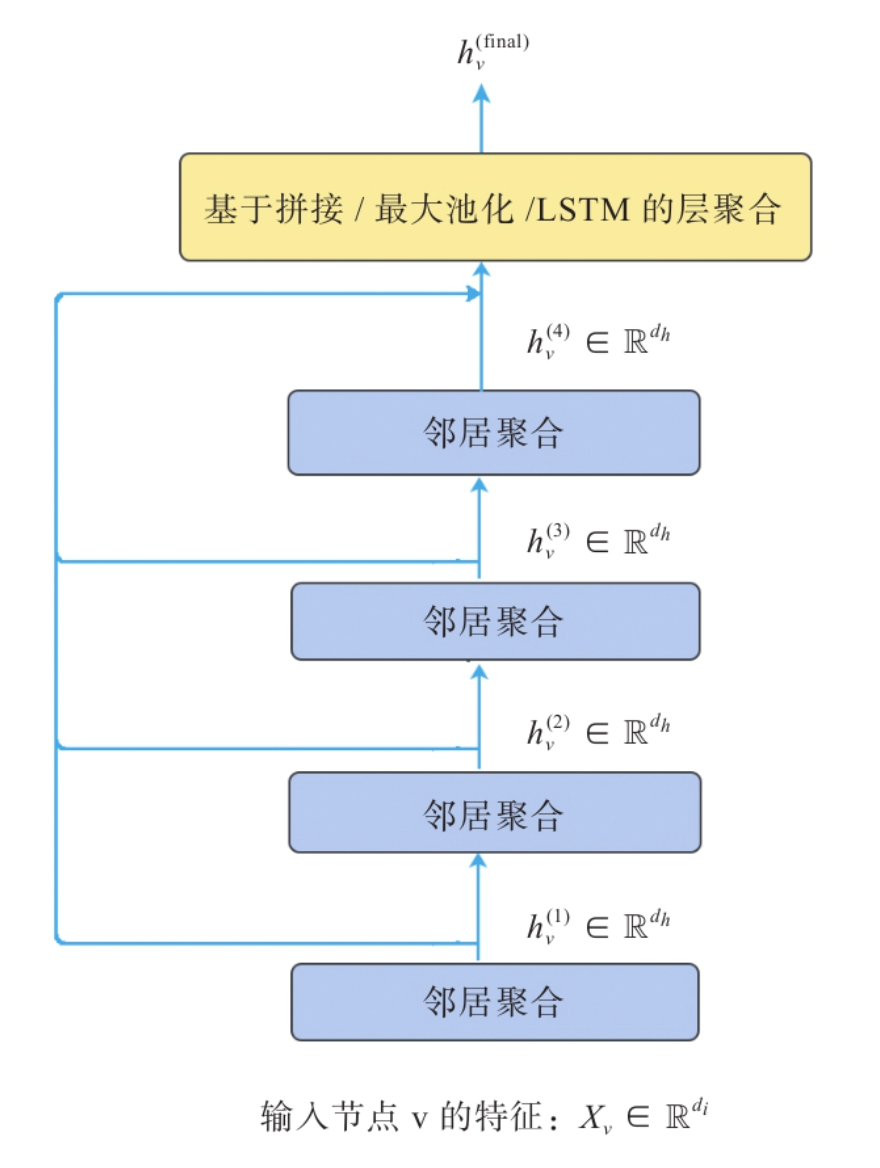
加入跳跃连接来聚合每层节点的输出，而不是直接使用最后一层节点的，对应的朴素想法就是可以给不同层加权重使得越近的邻居聚合的信息权重越大，当然也可以用更高级一点的方法。总之最后对于任意一个节点而言，既不会因为聚合半径过大而出现过平滑的问题，也不会因为聚合半径过小，使得节点的结构信息不能充分被学习。

还可以从频域角度出发，重新分配权重来增加\(\tilde A\)中节点自连接的权重，来加速/减缓模型低通滤波的效应。（这段书里写的比较简略，我没太懂，所以不细展开，当然这一段也是来自某paper的方法，感兴趣可以直接读原paper）。