【笔记】支持向量机

支持向量机

核心思想：最大化几何间隔

1. 线性可分支持向量机

1.1 名词解释

• 函数间隔 𝛾′
  • 感知机损失函数的分子。
  • 大于0分类正确，小于0分类错误。
• 几何间隔 𝛾
  感知机的损失函数就是几何间隔。

1.2 损失函数

初始损失函数是正确分类点到超平面的距离加和，但因为要使几何间隔最大，所以是最大化。约束条件𝑦𝑖(𝑤𝑇𝑥𝑖+𝑏)=𝛾′(𝑖)≥𝛾′(𝑖=1,2,...𝑚)，通常取𝛾′= 1。

1.3 损失函数的优化

1. 将有约束转为无约束损失函数，引入拉格朗日算子𝛼。
2. 转为解对偶形式。
3. 首先分别计算对偶式对𝑤和𝑏的偏导。
4. 带回原式后，只剩变量𝛼。
5. 通过SMO算法求得𝛼。
6. 根据第三步求导得出的关系式求出𝑤。
7. 求出𝑏。
   

2. 线性支持向量机

当数据集汇中出现了少量的异常点，导致线性不可分的时候，线性可分支持向量机就无能为力了。此时，需要通过软间隔最大化方法，即线性支持向量机模型。

2.1 软间隔最大化

区别于线性可分支持向量机的硬间隔最大化，软间隔最大化引入松弛变量(𝜉𝑖 ≥ 0)。使样本点距支持向量的距离为1 - 𝜉𝑖。同时对于每一个松弛变量，又对应着一个代价𝜉𝑖。

2.2 损失函数

• 2.2.1 普通损失函数
  同线性可分支持向量机类似，但是因为引入了松弛变量，所以需要加上对应的代价。
  
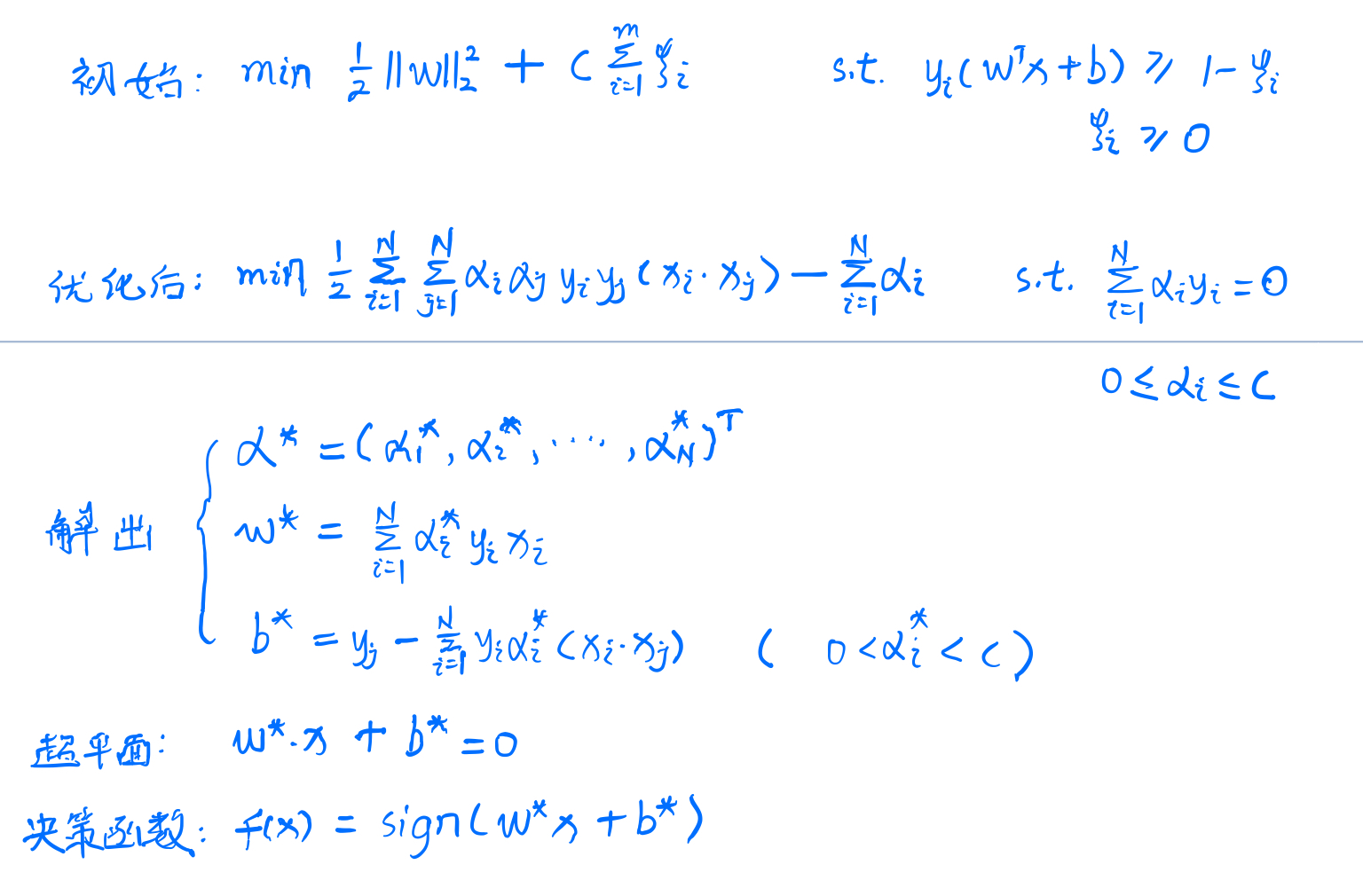
• 2.2.2 合叶损失函数
  这是对支持向量机的另一种解释。合叶损失函数：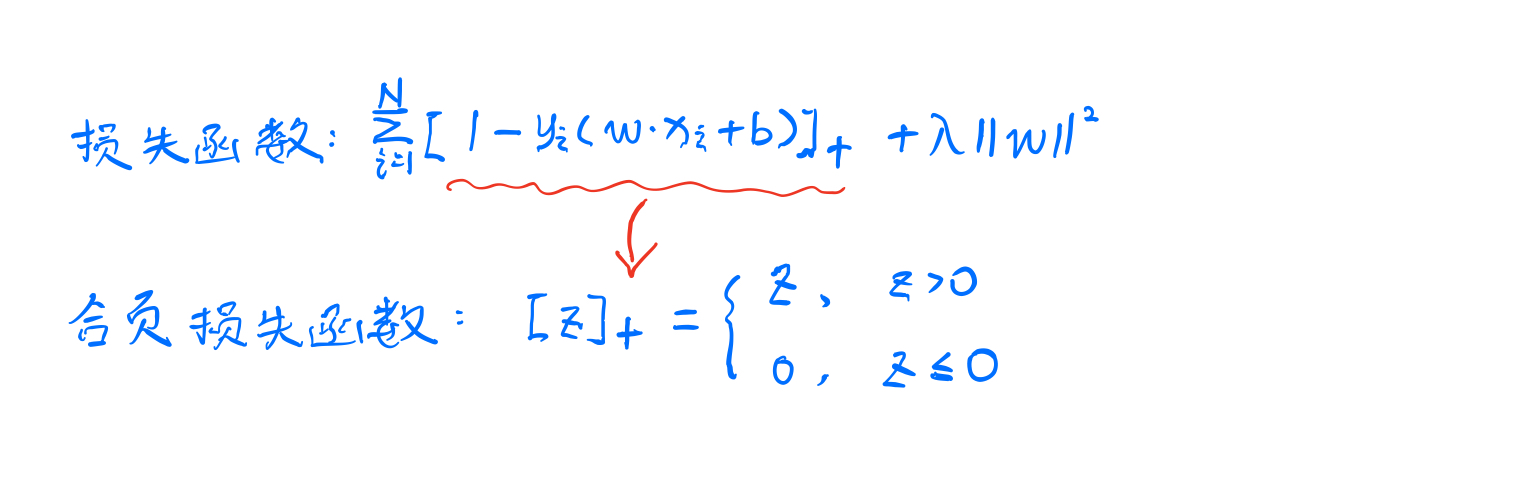
  当样本点被正确分类且函数间隔大于等于1时，损失为零。否则是1 − 𝑦(𝑤∙𝑥+𝑏)。相对于感知机的损失函数，合叶损失函数提出了更高的要求。

3. 非线形支持向量机

当数据完全线性不可分时，采用低维数据映射到高维的方法，使得可以在高维线性可分，从而转为前两节的问题。但仅简单的映射到高维，会导致计算量暴增，因此又引入核函数，可以在低维计算，却有高维的效果。

3.1 核函数定义

设𝜙是一个从输入空间𝜒(欧氏空间的子集或离散集合)到特征空间(希尔伯特空间)的映射。若存在函数K(x,z)，使得𝐾(𝑥,𝑧)=𝜙(𝑥)∙𝜙(𝑧)，则称K(x,z)是核函数，𝜙(𝑥)时映射函数。

3.2 损失函数

线性支持向量机可以看作特殊的(取线性核函数)非线性支持向量机。

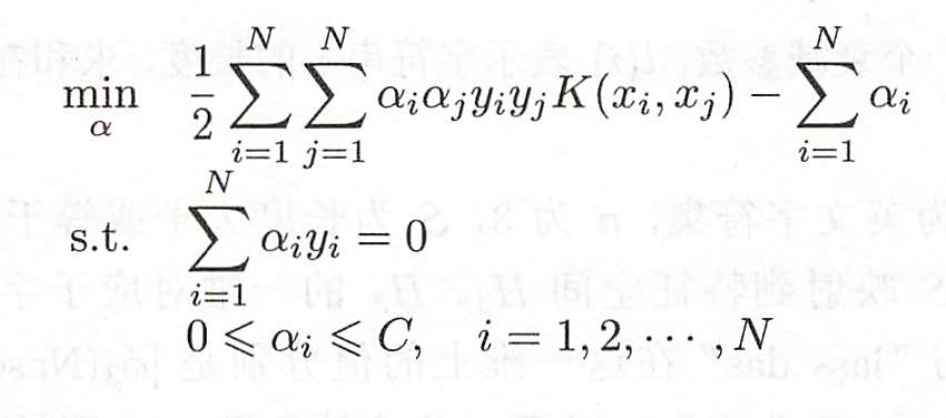
3.3 常用核函数

• 线性核函数 𝐾(𝑥,𝑧)=𝑥∙𝑧
• 多项式核函数 𝐾(𝑥,𝑧)=（𝛾𝑥∙𝑧+𝑟)^𝑑
• 高斯核函数 𝐾(𝑥,𝑧)=𝑒𝑥𝑝(−𝛾||𝑥−𝑧||^2)
• Sigmoid核函数 𝐾(𝑥,𝑧)=𝑡𝑎𝑛ℎ（𝛾𝑥∙𝑧+𝑟)