R语言(五)——横截面数据分类:经典方法(logistic、probit、判别分析)
目录
一、数据
脊柱数据(Column_2C.csv、Column_3C.csv)有两个版本,区别在于分为两类还是3类。数据可以从网站http://archive.ics.uci.edu/ml/datasets/Vertebral+Column下载,不过是.dat文件,需要进行相应的转换
参考我这篇博客Python将.dat文件转换成.csv文件。或者直接下载我上传的文件,是已经对格式和数据经过处理,可以直接进行分析的csv文件。
数据具有6个自变量(生物力学特征V1-V6,都是数量),和类别(V7)
两个数据内容分别为
| 类别 | 数量(人) | 代码 |
| C2 | ||
| 正常 | 100 | NO |
| 不正常 | 210 | AB |
| C3 | ||
| 正常 | 100 | NO |
| 椎间盘突出 | 60 | DH |
| 腰椎滑脱 | 150 | SL |
二、logistic回归
1.拟合
#logistic
#拟合
w2=read.csv("column_2C.csv")
a=glm(V7~.,w2,family="binomial") #默认logit连接函数
b=step(a) #做逐步回归筛选变量
summary(b) #结果汇总
在逐步回归过程中,变量3和4被淘汰,输出的AIC为188.95
2.预测
通过逐步回归或其他方法挑选的模型可能有助于解释模型,但不一定对预测有帮助。因此在我们分析的步骤中,还是利用逐步回归之前的a拟合模型
R自动把p(概率)作为排序靠后的类别的概率,于是运行代码levels(w2$V7)时,得到“AB”“NO”,p指的是NO的概率(R按照字典排序)
按照总误判率来寻找p值得阈值的函数如下:
BI=function(D,w,ff,fm="binomial"){
a=glm(ff,w,family=fm)
z=predict(a,w,type="response")
ee=NULL
for(p in seq(.1,.9,.01)){
u=rep(levels(w[,D])[2],nrow(w))
u[!(z>p)]=levels(w[,D])[1]
e=sum(u!=w[,D])/nrow(w)
#e=sum(u=="NO"&w[,D]=="AB")/sum(w[,D]=="AB")
ee=rbind(ee,c(p,e))
}
I=which(ee[,2]==min(ee[,2]))
P=ee[min(I),1]
return(ee[min(I),])
}其中D代表因变量是第几个变量,w为使用数据,ff是拟合公式,fm是模型。在此函数中,p值从0.1到0.9按0.01的间隔搜索。调用函数
p.2C=BI(7,w2,V7~.)得到阈值0.63,误判率0.1322。运行以下代码查看判别结果
#判别结果
D=7;p=p.2C[1];a=glm(V7~.,w2,family = "binomial")
z=(predict(a,w2,type="response")>p)
u=rep(levels(w2[,D])[2],nrow(w2))
u[!(z>p)]=levels(w2[,D])[1]
zz=table(w2[,7],u); #混淆矩阵
sum(diag(zz))/sum(zz) #正确率 混淆矩阵如图,正确率为0.871
混淆矩阵如图,正确率为0.871
还可以修改函数以改进效果,可以改变e的判别方式
三、probit回归
由于该数据的变量V6有出错信息,但我们又不愿意去掉该变量,因此代码中改用probit选项,此时不能计算AIC,也不能用逐步回归选择变量,但还是用BI()函数选择阈值
D=7;w=w2;ff=V7~.;fm=quasibinomial(link="probit")
pp.2C=BI(D,w2,ff,fm)
D=7;p=pp.2C[1];a=glm(V7~.,w2,family=fm)
summary(a)
z=(predict(a,w,type="response")>p)
u=rep(levels(w[,D])[2],nrow(w))
u[!(z>p)]=levels(w[,D])[1]
zz=table(w2[,7],u); #混淆矩阵
sum(diag(zz))/sum(zz) #正确率得到的probit回归的估计系数及近似正态z检验的结果和分类展示如下,可知训练出来的模型:

四、经典判别分析(线性、混合线性、灵活线性)
三者代码基本相似,只是部分地方有微小差别
#线性判别分析
library(MASS)
w2=read.csv("column_2C.csv")
a=lda(V7~.,data=w2)
b=predict(a,w2)$class
zz=table(w2[,7],b) #混淆矩阵
sum(diag(zz))/sum(zz) #正确率
#混合线性判别分析
library(mda)
w2=read.csv("column_2C.csv")
set.seed(1010)
a=mda(V7~.,data=w2)
b=predict(a,w2)
zz=table(w2[,7],b) #混淆矩阵
sum(diag(zz))/sum(zz) #正确率
#灵活线性判别分析
library(splines)
library(Matrix)
library(fda)
w2=read.csv("column_2C.csv")
set.seed(1010)
a=fda(V7~.,data=w2)
b=predict(a,w2)
zz=table(w2[,7],b) #混淆矩阵
sum(diag(zz))/sum(zz) #正确率五、交叉验证与比较
把数据随机分成Z份(此处Z=10),使用以下函数划分数据:
#产生数据集
Fold=function(Z=10,w,D,seed=7777){
n=nrow(w);d=1:n;dd=list()
e=levels(w[,D])
t=length(e)
set.seed(seed)
for(i in 1:t){
d0=d[w[,D]==e[i]]
j=length(d0)
ZT=rep(1:Z,ceiling(j/Z))[1:j]
id=cbind(sample(ZT,length(ZT)),d0)
dd[[i]]=id
}
#每个dd[[i]]是随机1:Z及i类的下标集组成的矩阵
mm=list()
for(i in 1:Z){
u=NULL
for(j in 1:t)u=c(u,dd[[j]][dd[[j]][,1]==i,2])
mm[[i]]=u #mm[[i]]为第i个下标集
}
return(mm) #输出Z个下标集
}运行logistic、lda、mda、fda判别分析的交叉验证,代码如下:
BI=function(D,w,ff,fm="binomial"){
a=glm(ff,w,family=fm)
z=predict(a,w,type="response")
ee=NULL
for(p in seq(.1,.9,.01)){
u=rep(levels(w[,D])[2],nrow(w))
u[!(z>p)]=levels(w[,D])[1]
e=sum(u!=w[,D])/nrow(w)
#e=sum(u=="NO"&w[,D]=="AB")/sum(w[,D]=="AB")
ee=rbind(ee,c(p,e))
}
I=which(ee[,2]==min(ee[,2]))
P=ee[min(I),1]
return(ee[min(I),])
}
#读数据
w=read.csv("column_3C.csv")
D=7;Z=10
mm=Fold(Z,w,D,7777)
ff=paste(names(w)[D],"~.",sep="")
ff=as.formula(ff) #logistic回归用最优阈值
p=BI(D,w,ff)[1]
ERROR=matrix(0,Z,4)
J=1
for(i in 1:Z){
m=mm[[i]]
a=glm(V7~.,w,family="binomial")
z=(predict(a,w[m,],type="response")>p) #测试集预测
u=rep(levels(w[m,D])[2],length(m))
u[!z]=levels(w[m,D])[1]
ERROR[i,J]=sum(w[m,D]!=u)/length(m)
}
J=J+1
for(i in 1:Z){
m=mm[[i]]
a=lda(ff,w[-m,])
ERROR[i,J]=sum(w[m,D]!=predict(a,w[m,])$class)/length(m)
}
J=J+1
for(i in 1:Z){
m=mm[[i]]
set.seed(1010)
a=mda(ff,w[-m,])
ERROR[i,J]=sum(w[m,D]!=predict(a,w[m,]))/length(m)
}
J=J+1
for(i in 1:Z){
m=mm[[i]]
a=fda(ff,w[-m,])
ERROR[i,J]=sum(w[m,D]!=predict(a,w[m,]))/length(m)
}
ERROR=data.frame(ERROR)
names(ERROR)=c("logistic","lda","mda","fda")
#ERROR
ME=apply(ERROR,2,mean)得到各种方法的误判率和平均误判率

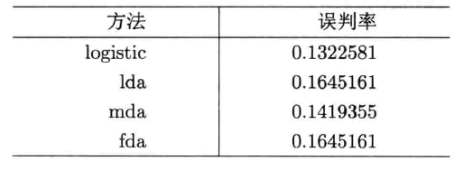
三分类数据同上,只需改变读取的数据集。同时三分类不能使用logistic方法


 浙公网安备 33010602011771号
浙公网安备 33010602011771号