《编程珠玑，字字珠玑》910读书笔记——代码优化

写在最前面的

再庞大复杂的代码编译器都能接受，编译器会变得越来越聪明，让我们原本的代码更加高效。但是代码执行的多变与不可预测性，如果编译器大肆“优化”，偶尔或者大胆的说“在大多数情况下”，会得到“聪明反被聪明误”的后果，所以编译器非常小心谨慎，一遇到不可预测后果的优化，它就会立即折返，停止这一步的优化工作，因为它不知道程序员的本意是什么，“它怕得罪你”。
程序员要编写容易优化的代码，以帮助编译器扫清障碍。关于代码优化，笔者特别喜欢《深入理解计算机系统》一书中的第五章，有兴趣的可以阅读一下。

代码优化小剖 

代码优化的方法总结了5种。

• 将函数展开，即内敛函数，以优化函数的调用。 《从简单的算法初探过程汇编》，过多的函数调用会导致极大的调用开销。所以，简单而且时常调用的函数建议内敛，例如swap，max，min。改用宏或者直接展开函数更好。 
  
  
• 消除循环的低效率
  这一点我感触比较深。
  

  toupper(* str)
      for i=[0,strlen(str))
          if(str[i]>='a' && str[i]<='z')
              str[i] += ('A'-'a')

  
  strlen的源码大概如下：
  

  strlen(* str) 
      len = 0
      while(*s!='\0')
          s++,len++
      return len

  所以toupper中对i的每一次检测，都调用了strlen，由此可见toupper的浪费由来。以前写程序一直采用上面的toupper，以为够简洁，就像第三点中的sum伪代码。  
  
  
• 减少不必要的存储器引用
  

  sum(* src,n,* dest)    //    src向量相加结果放入dest
      for i=[0,n)
          *dest += src + i

  代码如此简洁而有力，以前一直为这种风格而自豪。但它的缺点也是显然的，循环内部过多的引用dest地址：每次循环都要把dest地址内的数据取出到寄存器接，寄存器相加得到结果后，又从寄存器写入到dest地址，所以dest读n次，写n次。这有何必呢？读写浪费很浪费，下面的代码会不会好点：  
  

  sum(* src,n,* dest)    //    src向量相加结果放入dest
      temp = *dest;
      for i=[0,n)
          temp += src + i
      *dest = temp

  
  
• 循环展开 
  
  引用《深入理解》P348

  "首先，它减少了不直接有助于程序结果的操作的数量，例如循环索引计算和条件分支。其次，它提供了一些方法（重结合变换），可以进一步变化代码，减少整个计算中关键路径上的操作数量。"关键路径，书上对它的解释是执行一组机器指令所需时钟周期的一个下界。比如乘法和加法的周期，乘法就应该成为这组执行机器指令的关键路径。  
  
  什么是循环开销？比如：
  
  for i=(0,n]
  每一循环的开始都要对i做判断，以及对i自增，所以循环展开能降低这些开销。二路循环展开的伪代码：
  

  sum(* src,n,* dest)    //    src向量相加结果放入dest
      temp = *dest
      for i=[0,n-2+1),i+=2
          temp += src+i + src+i+1
      for i=[i,n),i+=1
          temp += src+i

  
  但是浮点的乘法没有得到效率的提高，是因为浮点乘法这个关键路径是循环展开的限制因素，即使循环展开，也需要执行n次的乘法。而有疑问，为什么整数乘法就能得到提高呢，那是因为编译器作了“重关联变换”的优化，改变了乘法的结合顺序（有兴趣看看下面的第6点，我带过了）。又有疑问了，为什么浮点不能作想整数乘法这样的优化呢？因为浮点乘法加法是不可结合的，记住“编译器怕得罪你”。 
  珠玑中第九章的顺序搜索就是用了这种优化。 
  
  
• 多个累积变量
  这是提高并行操作的方法，同时达到了循环展开的效果。 
  

  sum(* src,n,* dest)    //    src向量相加结果放入dest
      temp1 = *dest
      temp2 = 0
      for i=[0,n-2+1),i+=2
          temp1 += src+i    //    提高并行性，temp1和temp2可以并行计算而毫不牵连
          temp2 += src+i+1
      for i=[i,n),i+=1
          temp += src+i
      *dest = temp1+temp2
  //temp1和temp2的加法操作是两条关键路径，而两条关键路径各执行了n/2个操作。 

  同样，乘法也能得到效率的提高。注意循环寄存器有两个，数据相关降低，两个循环寄存器的运算是并行的。
  

 

关于第六种优化方法——重新结合变换 

书上还有说第六种优化——重新结合变换，如果大胆对浮点运算进行此类优化，性能有很大的提高。之所以没有标号，是因为笔者也不太能说清楚，说说笔者的理解。

sum(* src,n,* dest)    //    src向量相加结果放入dest
    temp = *dest
    for i=[0,n-2+1),i+=2
        temp = temp * (src+i * src+i+1)    //    假设原来是temp = (temp * src+i) * src+i+1
    for i=[i,n),i+=1
        temp += src+i

 

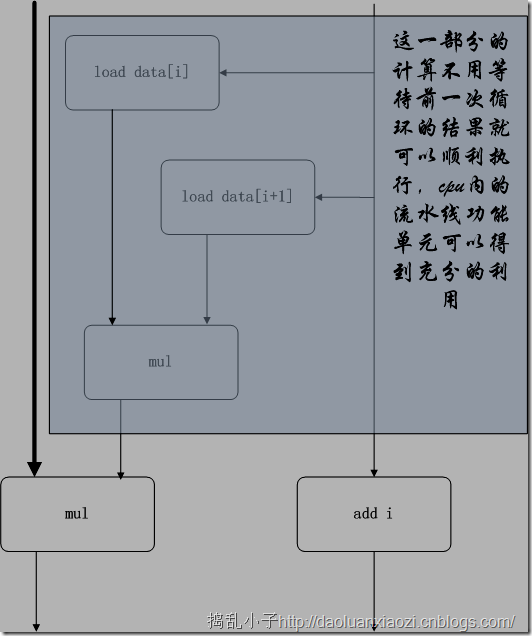
我的理解可以结合下图，下图是乘法的图，同样可以换成加法的图：

注意是temp = temp * (src+i * src+i+1)的图，而不是temp = (temp * src+i) * src+i+1的图，后者大家可以自己手动画画。

 

哈哈，书上说：未经训练的人员，上面的两条语句是一样的，“捣乱笑而不语啊！”我的理解是虽然循环寄存器只有一个，但是temp = temp * (src+i * src+i+1)中(src+i * src+i+1)的计算不依赖于循环寄存器的值即temp的值，而temp = (temp * src+i) * src+i+1会对temp产生依赖，结合顺序会对循环寄存器进行产生依赖，因此前者可以增加计算的并行性。 

神马？什么是循环寄存器？对于某些循环来说，有些寄存器既作为源值又作为目的，一次循环的结果会在下一次循环中用到。循环寄存器之间的关联越大，那么，这种关联将是性能提升的瓶颈。 

简单举个例子：

sum(* src,n,* dest)    //    src向量相加结果放入dest
    temp = *dest;
    for i=[0,n)
        temp += src + i
    *dest = temp

那么temp所在寄存器就是所谓的“循环寄存器”，它使得每一次循环都有很大的关联，所以，temp的加法操作（抑或是乘法操作）是关键路径，这也就是为什么累积变量能够提高程序的性能，它有两个循环寄存器，降低了循环关联。 

    《珠玑》第九章的代码优化，印象比较深的：

1.     整数取模 
2.     函数内敛 
3.     循环展开 

跟上面的内容差不多。 

关于哨兵

哨兵就是能帮助程序检测数组边界的东西，简化了数组边界的检测，从而使代码更加清晰简便。记得一开始接触哨兵是在顺序表查找的时候。

search(* arr,n,data)
    arr[n] = data
    for i=[0,n)    arr[i]!=data    //肯定会遇到data
        do nothing in for
    if(i==n)    return -1
    return i;

再来就是直接插入排序；如果不设置哨兵，不仅要检测下标是否下溢，而且要检测只有当满足arr[j]>data,才后移，这里会有两个判断。

insert_sort
    for i=[0,n)
        if arr[i]>arr[i+1]
            arr[0] = arr[i+1]                    //哨兵
            for j=[i+1)    arr[j]>arr[0]        //相比常规版本，只做n次判断。
                arr[j] = a[j-1],j--
            arr[j+1] = arr[0]

另外，用单链表存储一组顺序数据，对于这种问题，一般的单链表插入，都要考虑头插法和尾插法的情况，其他情况的代码可以是一致的；如果能够为单链表的最后添加哨兵，应该可以很大程度上简化代码。下面的代码比一般的单链表插入简洁而且应该更高效：

pre_insert:把maxval放置链表的最后
insert(* first,data)
    p = first->next
    while(p)
        if data < q->data
            end while
        p = p->next;
    p = new node(data,p)

《珠玑》第9章第8小题，“如何在程序中使用哨兵来找出数组中的最大元素”？
如果没有“哨兵”，大致的想法就是用一个变量max来存储数组的第一个值，然后从第二个开始“逐个”检验是否>max。加上循环中的下标检验，共有2n次的检测。
放置哨兵的做法：在数组的最后放置“已经找到的最大的元素”，然后逐个检验，

find_max(* arr)
    i = 0
    max = arr[i]
    while(i!=n)
        max = arr[i]
        arr[n] = max
        i++
        while(arr[i]<max)    //因为有哨兵的存在，此循环必定可以终结。
            i++

除非arr是严格递增或者每个元素值相等，否则总的检测次数会<2n。总之在考虑边界检测的时候，不妨考虑下用在边界上放置哨兵来简化清晰代码。

 

总结 

不知道这些优化，在以后的做题能不能奏效了。对于一些程序，笔者认为上面的优化是无关痛痒的，或许编程的技巧会更突显重要性，当完成了大部分程序，而后考虑上面的优化也不为过；但养成“优化”的习惯不失为一个优秀程序员的品质。（以上是笔者的学习笔记，需要更深入了解上面的内容，阅读原著或许收益更多。）关于珠玑的第十章，笔者实在无能为力 - =，只写了第九章。

本文完 Sunday, April 15, 2012 

捣乱小子 http://daoluanxiaozi.cnblogs.com/