1.学习总结
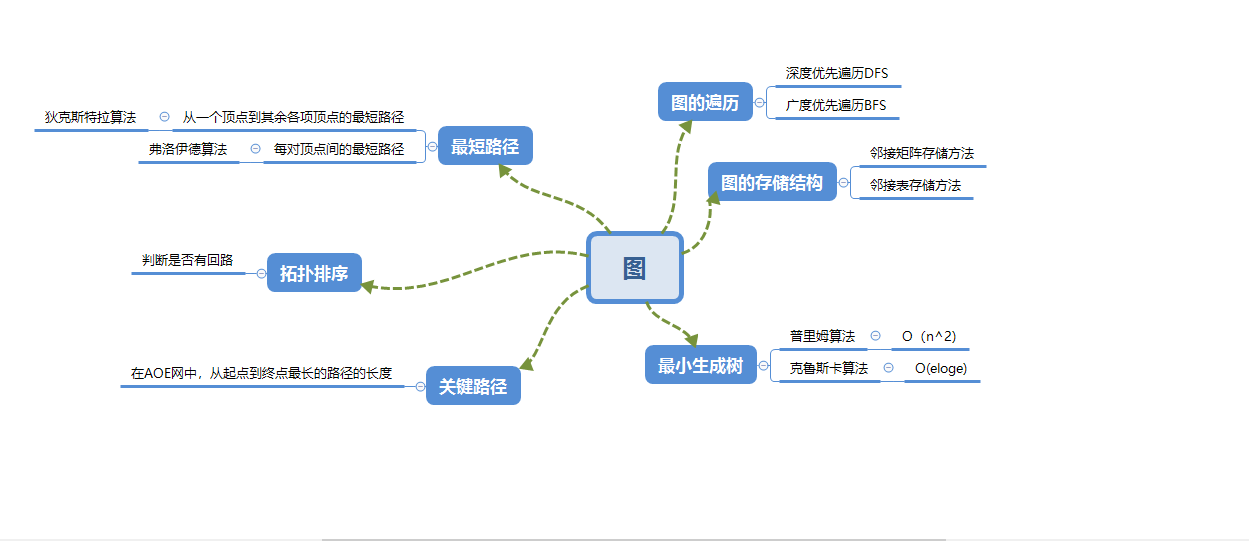
1.1图的思维导图
1.2 图结构学习体会
深度遍历算法：
访问顶点v
依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径想通的顶点都被访问；
若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所以顶点均被访问过为止；
通过递归实现
广度遍历算法：
访问顶点V
访问V的所有未被访问的邻接点；
依次从这些邻接点出发，访问它们所有未被访问的邻接点，直到图中所以访问过的顶点的邻接都被访问；
通过队列实现
Prim和Kruscal算法：
最小生成树可以使用prim算法和Kruscal算法实现，对于稀疏图来说，用Kruscal算法效率更好，加上并查集可对其进行优化；
Kruscal在所有边中不断寻找最小的边，prim在U和V两个集合之间寻找最小的连接，共同点是构造过程中都不能形成环；
Prim适合稠密图，因此通常使用邻接矩阵存储，而Kruscal多用邻接表，稠密图Prim>Kruscal,稀疏图Kruscal>Prim;
Prim适合点少边多，Kruscal适合边多点少；
Dijkstra算法：
贪心算法，最短路径问题
以起始点为中心向外层层扩展，直到扩展到终点为止；
拓扑排序算法：
只有有向无环图才可以进行拓扑排序
从AOE网中选择一个没有前驱的顶点（该顶点的入度为0）并且输出它；
从网中删去该顶点，并且删去从该顶点发出的全部有向边；
重复上述两步，直到剩余的网中不再存在没有前驱的顶点为止；
2.PTA实验作业
2.1 题目1：图着色问题
2.2 设计思路
定义变量i，j
定义变量 v顶点数 e边数 k颜色数
定义变量 a,b为两个端点的编号 num为方案的个数 数组color[]
vector和 set
输入v e k
for i=0 to e
输入a b并添加到容器末尾
输入 num
while(num--)
bool flag=true
for i=1 to v
输入数组color[i]并插入容器
if 容器大小 不等于k
flag=false
for i=1 to v
for j=0 to mp[i].size()
if color[i]等于color[mp[i][j]]
flag=false
break
if非flag break
if flag
输出Yes
else
输出No
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）
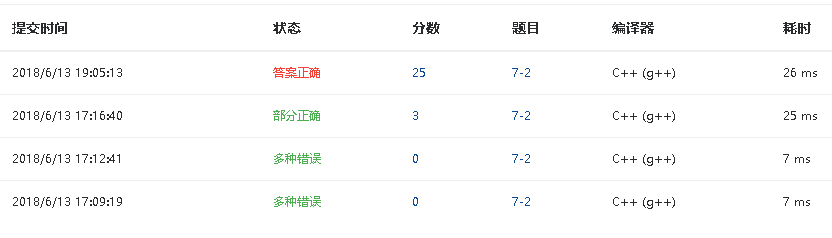
2.4 PTA提交列表说明。
2.1 题目2：排座位
2.2 设计思路
find()
join(int x,int y)
将两个集合合并
定义fx=find(x);
定义 fy=find(y);
if不在一个集合
pre[fx]=fy;
same(int x,int y)
判断两个元素是否在同一个集合中
if 在
返回 true;
else
返回 false
main()
定义 a,b,c,n,m,t,i;
输入n m t
for i=1 to n
pre[i]=i;
for i=1 to m
输入 a b c
记录直接的对应关系
if c等于1
调用函数join(a,b)判断间接关系
for i=1 to t
输入 a b
if 是朋友 输出 No problem
else if 有敌对也有共同朋友 输出OK but...
else if 不是朋友，但也不敌对 输出OK
else if 敌对关系No way
end
2.3 代码截图
2.4 PTA提交列表说明。
2.1 题目3：
3.截图本周题目集的PTA最后排名
3.1 PTA排名
3.2 我的总分：140
4. 阅读代码（必做，1分）
