树形DP
Up and Down DP
如何求解从一个点到其它地方的路径长度信息?
点分治
可以使用 Up and Down DP
将路径分成两类, 向上走以及向下走, 进行简单的维护, 进行两次 \(dfs\)
先计算树的情况, 使用 Up and Down DP
\(ans_u = \frac{down_n \times son_u + up_u \times fa_u}{son_u + fa_u}\)
先一遍 \(dfs\) 求解 \(down\)
\(down_u = \frac{1}{son_u} \sum (down_v + w_{u, v})\)
再一遍 \(dfs\) 求解 \(up\)
\(up_u = w_{u, k} + \frac{up_k \times fa_k + down_k \times son_k - down_u - w_{u, k}}{fa_k + son_k - 1}\)
是不是非常优美的转移式子
基环树环很小, 直接暴力枚举计算 \(up\) 就可以了
考虑 \(B\) 开头的最小生成树算法
那么我们需要求解一个连通块向外连的最小边, 我们也就是要求一个点向外连的最小边
使用 Up and Down DP 对于可能连通块相等的情况, 可以再记录一个最小值
树上背包
和背包一样
主要说一下的复杂度 \(O(nm)\)
注意要对子树的大小取 \(min\)
如果不取的话, 复杂度其实是 \(O(nm^2)\)
树上依赖性背包
如果不能对子树的大小取 \(min\) 呢
我们两个数组的卷积复杂度是 \(O(m \times m)\) 的
但如果是一个数组与一个值的复杂度就是 \(O(m)\) 的
若干个值卷起来就是 \(O(n \times m)\) 的
我们显然可以通过控制 \(n\) 来到达一个比较好的复杂度, 所以有下边的思路
我们只要求根的话, 我们有一种做法
我们想要只卷 \(n\) 次
就是考虑 \(dfs\) 序
我们设 \(f_{i, j}\) 表示 \(dfs\) 序 \(\ge i\) 的方案
考虑如果选择可以从 \([i + 1, n]\) 转移
如果不选择可以从 \([i + sz_i, n]\) 转移
这是 \(dfs\) 序的特性
复杂度 \(O(n)\)
如果需要求很多点呢?
- 点分治
这个比较显然
复杂度 \(O(nmlogn)\)
- dus on tree
我们要用 \(f_{i, j}\) 算出 \([i, i + sz_i - 1]\) 的方案
它的若干个儿子把序列分成了若干份, 我们肯定也想要 \(O(n \times m)\) 样子的复杂度
所以, 我们考虑把一个一个的值卷起来, 不难想到 dsu_on_tree
复杂度就是 \(O(nmlogn)\)
一类统计链的树形 DP
核心思想
就是分情况讨论, 考虑当前节点与当前节点儿子之间的贡献, 把复杂的问题拆成比较简单的几个问题
例1
给定一棵 \(n\) 个点的树, 找到树上的两条边不相交的路径, 使得删去路径上的所有点和边后剩下的连通块数量最多, 输出最大个数
\(n \le 5 \times 10^5\)
考虑树形 \(DP\) 考虑当前节点与他的儿子节点构成答案的所有可能情况
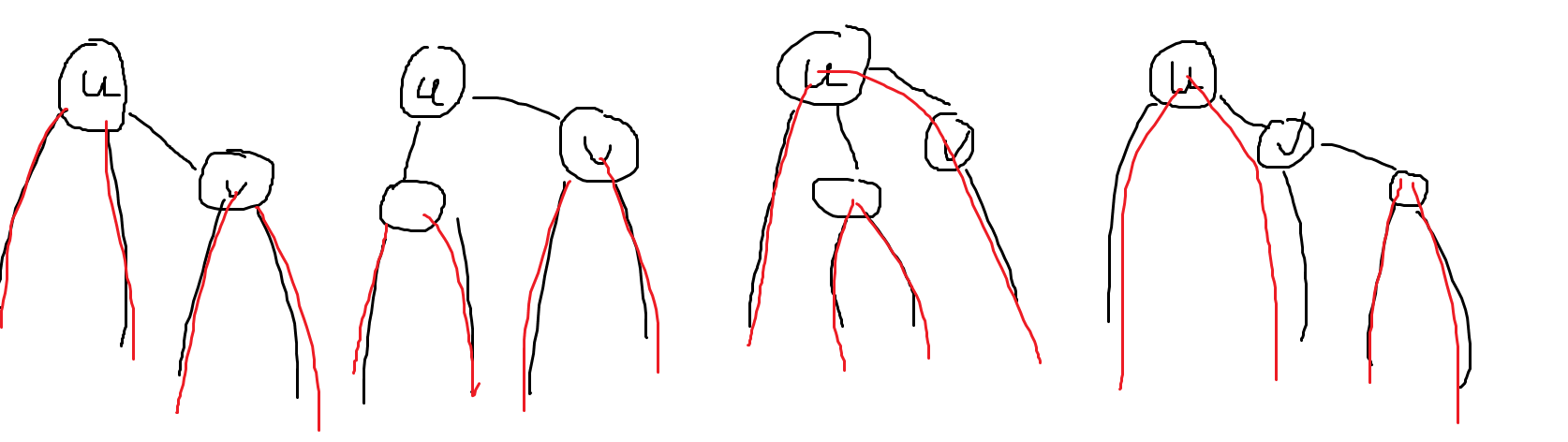
这三种情况
发现第一二种情况只需要维护经过自己的一条最优方案, 和不经过自己的子树内的一条最优方案
但是第三, 四种情况, 分别可以通过 \(u\) 中的一条经过 \(u\) 链和 \(u\) 子树中的一个方案加上 \(v\) 中的一条经过 \(v\) 的链||\(u\) 中的一条 经过 \(u\) 链和 \(v\) 中的一条经过 \(v\) 的链加上 \(v\) 子树内的方案拼接而成
所以设如下状态
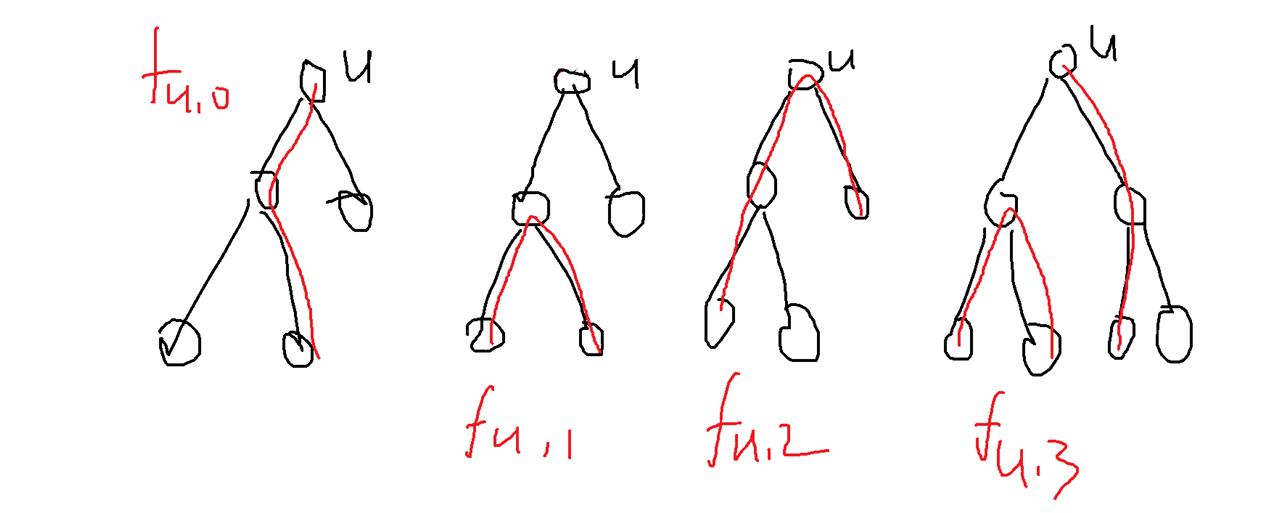
设 \(f_{u, 0}\) 是为了更好的转移
那么我们来考虑如何维护这个东西吧
先是 \(f_{u, 0}, f_{u, 1}, f_{u, 2}\)
\(f_{u, 0} = \max\{f_{v, 0} + son_u - 1\}\)
\(f_{u, 1} = \max\{f_{v, 1}, f_{v, 2} + 1\}\)
\(f_{u, 2} = \max\{f_{v,0} + f_{u, 0} + 1\}\)
都是比较容易理解的
比较复杂度是 \(f_{u, 3}\)
考虑链是那里的, 不是 \(v\) 子树的:
\(f_{u, 3} = \max\{f_{v, 1} + f_{u, 0} - 1, f_{v, 2} + f_{u, 0} - 1\}\)
是 \(v\) 子树的, 再考虑 另一条最优路径是哪里的, 不是 \(v\) 子树中的
\(f_{u, 3} = \max\{f_{v, 0} + f_{u, 2} - 1\}\)
剩下一种需要注意一下, 因为 \(f_{u, 1}\) 我们并不知道它是 \(u\) 的直系儿子, 还是二代以后的, 所以我们并不好处理连通块的个数, 所以采用 \(tmp = \max\{f_{v, 1}, f_{v, 2}\}\)
\(f_{u, 3} = \max\{f_{v, 0} + tmp + son_u - 2 \}\)
是 \(v\) 子树中的
\(f_{u, 3} = \max\{f_{v, 3} + son_u - 1\}\)
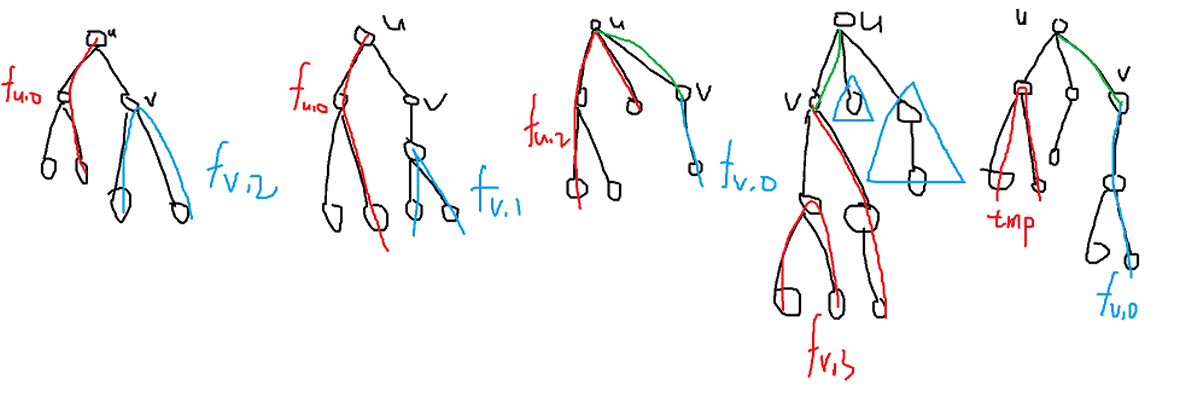
由于链可以退化成点, 路径可以退化成链
\(f_{u, 2} = \max\{f_{u, 0}\}, f_{u, 3} = \max\{ f_{u, 2}\}\)
然后是统计答案
第一二种情况
\(f_{u, 1} + f_{v, 2}\)
\(f_{u, 1} + f_{v, 1} - 1\)
\(f_{u, 2} + f_{v, 1} - [u==1]\)
\(f_{u, 2} + f_{v, 2} - [u==1]\)
第三种情况
\(f_{u, 3} + f_{v, 0} - [u==1]\)
第四种情况
\(f_{v, 3} + f_{u, 0} - [u==1]\)
初始化方面
\(f_{u, 0} = f_{u, 2} = f_{u, 3} = son_u, f_{u, 1} = 1\)
例2
在树上寻找 \(k\) 条点不相交链,并且最大化这 \(k\) 条链的边权之和
前边是 wqs二分
后边自己想, 和上边是差不多的
拆边贡献
这是树形 \(DP\) 常见的
换根 \(DP\)
一遍 \(dfs\) 求出一些信息以及此时根的答案, 第二遍 \(dfs\) 开始换根



 浙公网安备 33010602011771号
浙公网安备 33010602011771号