矩阵快速幂

矩阵可以用二维数组或者vector数组来存储，但是vector数组的操作可能会有点慢，遇到TLE且矩阵大小比较固定的题目，及时转换到二维数组。至于快速幂的实现，与普通整数快速幂思想一样。一个简单例题POJ3734，用vector数组实现

#include<stdio.h>
#include<vector>
using namespace std;
typedef vector<int> vec;
typedef vector<vec> mat;
typedef long long ll;
const int mod=10007;
mat mul(mat &A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++){
        for(int k=0;k<B.size();k++){
            for(int j=0;j<B[0].size();j++){
                C[i][j]=(C[i][j]+A[i][k]*B[k][j])%mod;
            }
        }
    }
    return C;
}
mat pow(mat A,int n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++){
        B[i][i]=1;
    }
    while(n!=0){
        if(n%2==1) B=mul(B,A);
        A=mul(A,A);
        n/=2;
    }
    return B;
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int n;
        scanf("%d",&n);
        mat A(3,vec(3));
        A[0][0]=2;A[0][1]=1;A[0][2]=0;
        A[1][0]=2;A[1][1]=2;A[1][2]=2;
        A[2][0]=0;A[2][1]=1;A[2][2]=2;
        A=pow(A,n);
        printf("%d\n",A[0][0]);
    }
    return 0;
}

搞清楚矩阵乘法的步骤，这一部分代码就比较容易。难点在于发现规律，以及将规律转化为矩阵。对于普遍的递推式，有矩阵形式：

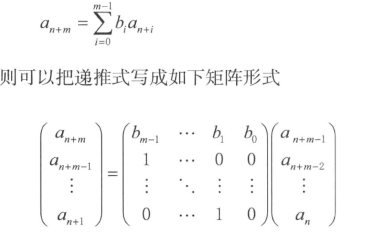
若是递推式中有常数项，对应地需要扩展矩阵：

POJ3735，对表中元素执行一系列加减、清空、置换的操作，并重复多次，每一次指令可以用矩阵进行记录，计算矩阵幂即可求解。但是这里的A、T与不同矩阵不同，需要扩展，T有n+1个元素，第一个为1其他为0；A是(n+1)*(n+1)单位矩阵，根据操作进行变换

#include<stdio.h>
typedef long long ll;
const int N=105;
struct mat{
    ll a[N][N];
    void init(){
        for(int i=0;i<N;i++){
            for(int j=0;j<N;j++){
                a[i][j]=0;
            }
        }
    }
};
int n,m,k;
mat mul(mat A,mat B){
    mat C;
    C.init();
    for(int i=0;i<=n;i++){
        for(int k=0;k<=n;k++){
            if(A.a[i][k]){
                for(int j=0;j<=n;j++){
                    C.a[i][j]+=A.a[i][k]*B.a[k][j];
                }
            }
        }
    }
    return C;
}
mat pow(mat A,int x){
    mat B;
    B.init();
    for(int i=0;i<=n;i++){
        B.a[i][i]=1;
    }
    while(x!=0){
        if(x%2==1) B=mul(B,A);
        A=mul(A,A);
        x/=2;
    }
    return B;
}
int main(){
    while(scanf("%d%d%d",&n,&m,&k)!=EOF){
        if(n==0&&m==0&&k==0) break;
        mat A;
        A.init();
        for(int i=0;i<=n;i++) A.a[i][i]=1;
        char s[5];
        int a,b;
        while(k--){
            scanf("%s%d",s,&a);
            if(s[0]=='g') A.a[0][a]++;
            else if(s[0]=='e'){
                for(int i=0;i<=n;i++) A.a[i][a]=0;
            }
            else{
                scanf("%d",&b);
                for(int i=0;i<=n;i++){
                    int t=A.a[i][a];
                    A.a[i][a]=A.a[i][b];
                    A.a[i][b]=t;
                }
            }
        }

        mat T;
        T.init();
        T.a[0][0]=1;
        T=mul(T,pow(A,m));
        for(int i=1;i<=n;i++){
            printf("%lld ",T.a[0][i]);
        }
        printf("\n");
    }
    return 0;
}

POJ3233，矩阵幂下一种独特的类型，求S=A+A²+A³+...+Aⁿ。

最后再记录一道题，在图中求长度为k的路径总数。k=1时，邻接矩阵就是最后的答案矩阵，遍历矩阵求和即可。k>=1，最后的答案矩阵是邻接矩阵的k次幂。