树、二叉树、查找算法总结

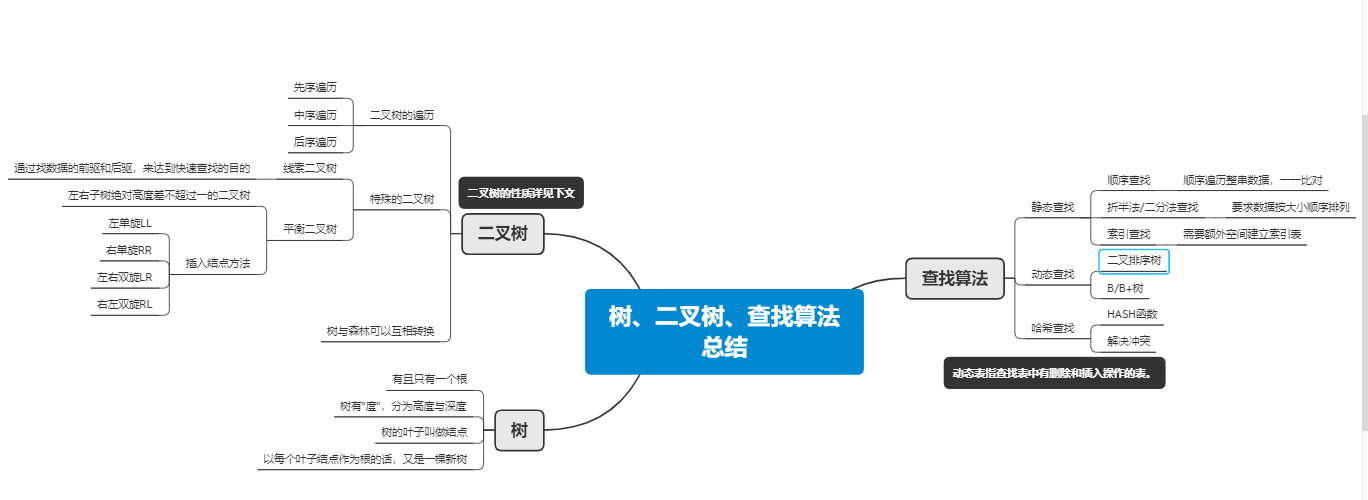
一、思维导图

二、重要概念

1、二叉树的特殊性质

• 在二叉树的第ｉ（ｉ>=１）层最多有２＾(ｉ - １)个结点。
• 对于任一棵非空二叉树，若设其叶结点数为n0，度为2的非叶结点数为n2，则存在ｎ0 = ｎ2 ＋１。
• 深度为k(k>=0)的二叉树最少有k个结点，最多有２＾ｋ－１个结点。 、
• 带权路径最短的二叉树称为哈夫曼树或最优二叉树。

2、二叉树的遍历要点

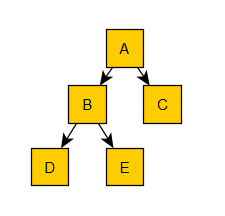
• 先序遍历：ABDEC(根左右)
• 中序遍历：DBEAC（左根右）
• 后序遍历：DEBCA（左右根）

3、解决哈希冲突的方法

a、使用线性探查法时，若遇到冲突，则按顺序向下继续查找，直到发现可以放置的空位为止。

• 优点：操作简单
• 缺点：时间复杂度可能会很大

b、使用拉链发时，若遇到冲突，可以使用链表来处理冲突

• 解决思想：每个哈希表节点都有一个next指针，多个哈希表节点可以用next指针构成一个单向链表，被分配到同一个索引上的多个节点，都可以用这个单向链表连接在一起。

三、疑难解惑

1、查找失败时的ASL计算

• 在计算散列表的ASL值时，需要确认散列表长度。从待查元素开始，一直查到遇到的“第一个空位”，这算一次失败的查找，查了几次需要计算清楚。

2、B树/B+树的特征有哪些？在数据库索引中为什么不用二叉树？

• 查阅资料可知，二叉树的查找速度和比较次数都是最小的，但在实际应用中，我们却更多地使用B树/B+树。
• 在数据库搜索的实际应用中，我们需要的是一棵“矮胖”的树，即高度小，孩子结点多的树。