一、学习总结
1.1 思维导图
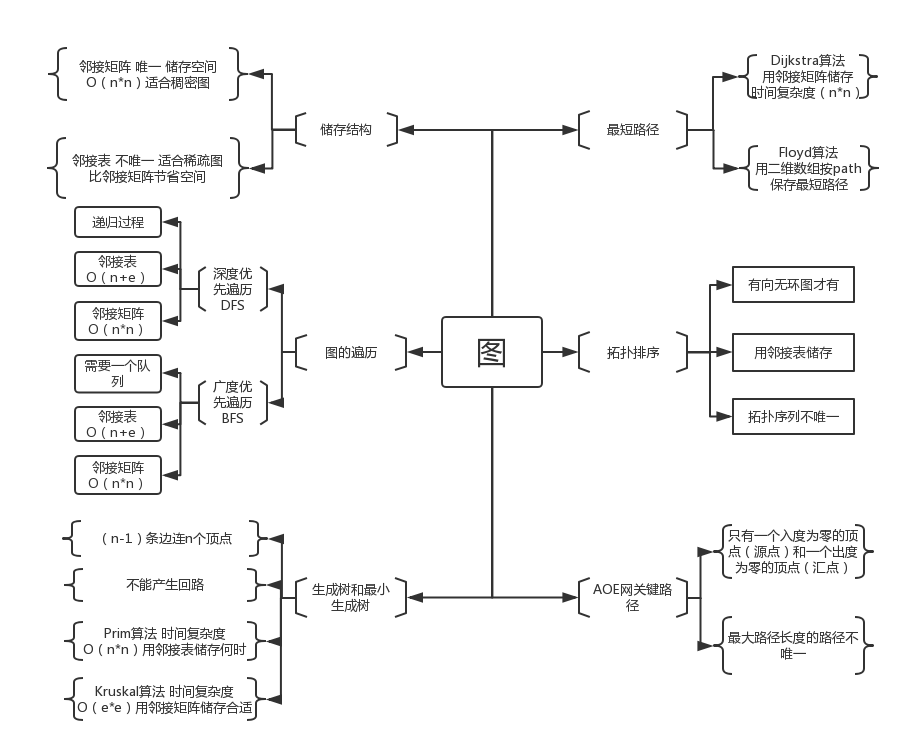
1.2 图结构学习体会
(1)、深度遍历算法和广度遍历算法:这两种遍历都可以遍历出整个图,但是深度遍历对于新手来说还是有一点点小难度,但是熟悉了之后发现也就那样,对吧。但是还是需要去认真去理解。
(2)、Prim和Kruscal算法:这两种算法都是算最小生成树的,Krusca是直接从最小权重连接,而Prim是直接连接的。
(3)、Dijkstra算法和Foled算法:Foled算法到后面可以更改相对应的最小路径而Dijkstra算法一旦确定就无法更改。
(4)、拓扑排序算法:这个拓扑排序不允许有回路,而且只能在有向图里。
二、PTA实验作业
1.7-1 图着色问题
(1)设计思路
使用图的邻接表存储结构,再顶点信息和边信息中加上一个变量存储颜色信息。先建图,完善图的信息。输入顶点颜色种类时,通过循环判断之前是否出现过相同颜色来计算颜色数量。若颜色数量与题目要求一致,再判断相邻顶点颜色是否相同。判断方法为:若头节点颜色与其某一nextarc节点颜色一致,则是非解。反之,若每一个头节点都与其所有的nextarc节点颜色不同,则是解。
(2)代码截图
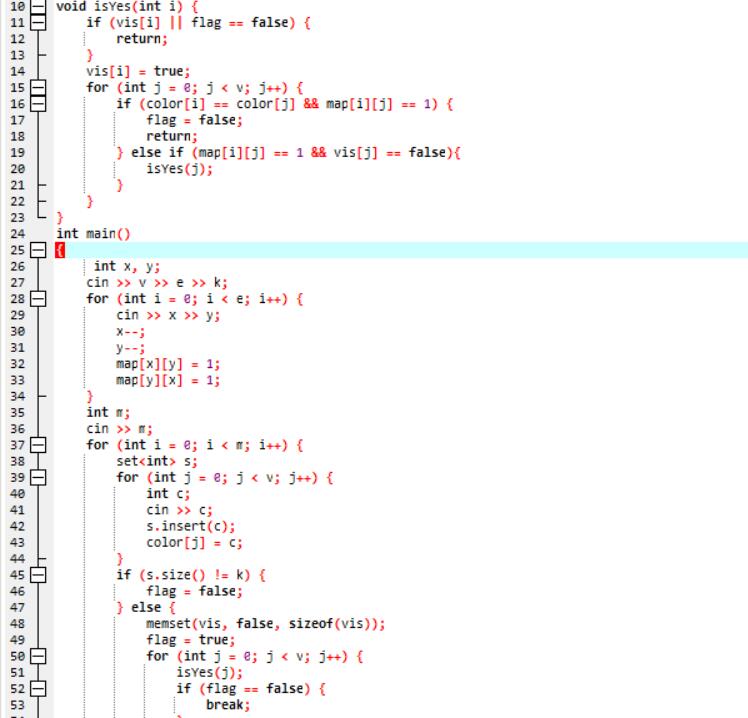
(3)PTA提交列表说明
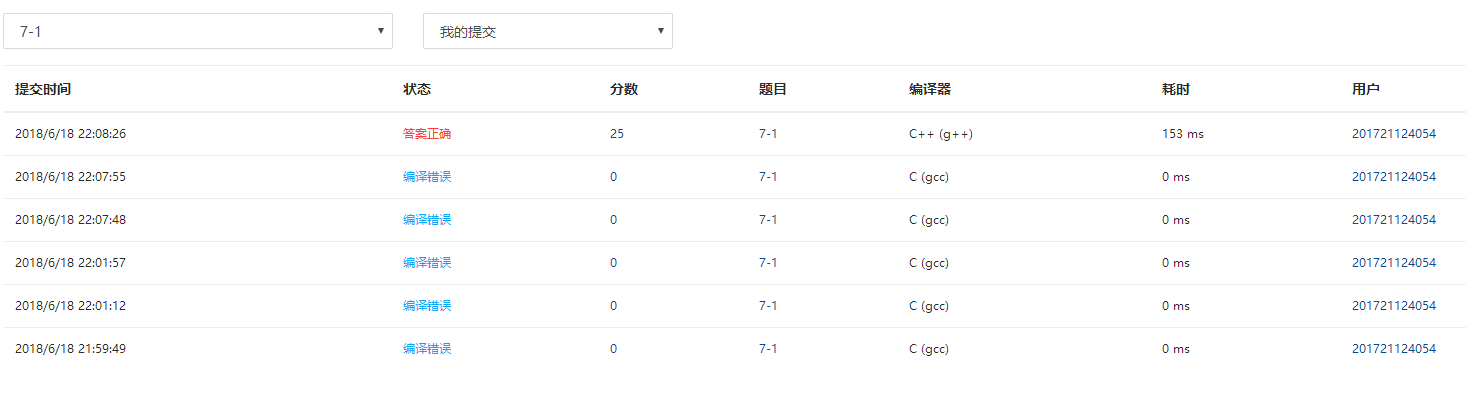
不能熟练使用set和memset导致编译错误,还有忘记改成C++。
2、7-2 排座位
(1)设计思路
初始化并查集;
判断两人是否为朋友;
是记录是朋友 ;否记录是敌人;
输入两个宾客;
有共同朋友就输出同一张桌子;
(2)代码截图
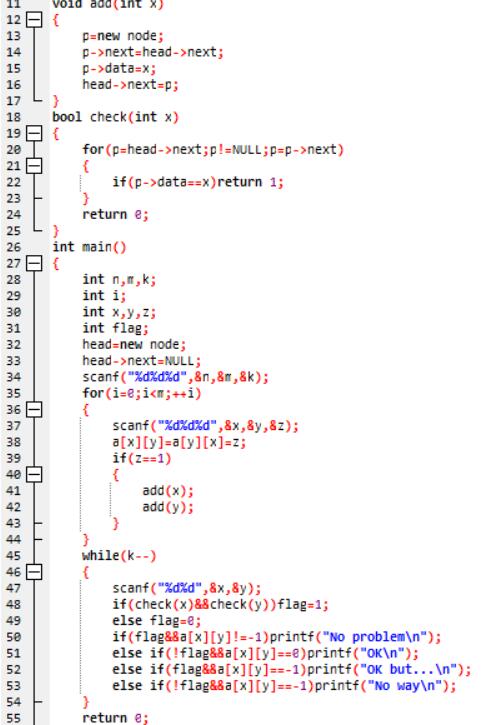
(3)PTA提交列表说明

情况遗漏,首次检查未发现
3、7-4 公路村村通
(1)设计思路
把这个道路的邻接矩阵建立起来
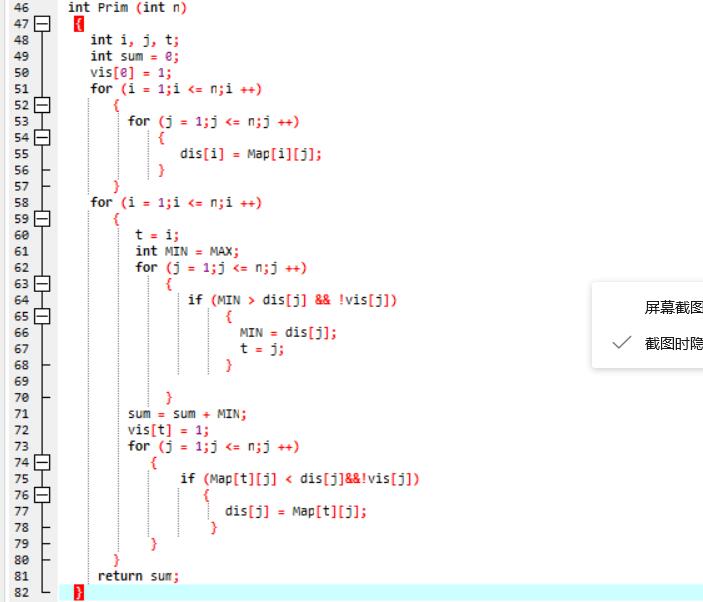
用Prim算法算出最小权重的和,
如果可以遍历到所有的城镇则输出需要的钱,
如果没有则输出Impossible。
(2)代码截图
(3)PTA提交列表说明
三、PTA最后排名

四、阅读代码
Dijkstra算法
首先,引进一个辅助向量D,它的每个分量D表示当前所找到的从始点v到每个终点vi的最短路径的长度。如D[3]=2表示从始点v到终点3的路径相对最小长度为2。这里强调相对就是说在算法过程中D的值是在不断逼近最终结果但在过程中不一定就等于最短路径长度。它的初始状态为:若从v到vi有弧,则D为弧上的权值;否则置D为∞。显然,长度为 D[j]=Min{D | vi∈V} 的路径就是从v出发的长度最短的一条最短路径。此路径为(v,vj)。 那么,下一条长度次短的最短路径是哪一条呢?假设该次短路径的终点是vk,则可想而知,这条路径或者是(v,vk),或者是(v,vj,vk)。它的长度或者是从v到vk的弧上的权值,或者是D[j]和从vj到vk的弧上的权值之和。 一般情况下,假设S为已求得最短路径的终点的集合,则可证明:下一条最短路径(设其终点为X)或者是弧(v,x),或者是中间只经过S中的顶点而最后到达顶点X的路径。因此,下一条长度次短的最短路径的长度必是D[j]=Min{D | vi∈V-S} 其中,D或者是弧(v,vi)上的权值,或者是D[k](vk∈S)和弧(vk,vi)上的权值之和。迪杰斯特拉算法描述如下: 1)arcs表示弧上的权值。若不存在,则置arcs为∞(在本程序中为MAXCOST)。S为已找到从v出发的最短路径的终点的集合,初始状态为空集。那么,从v出发到图上其余各顶点vi可能达到的最短路径长度的初值为D=arcs[Locate Vex(G,v),i] vi∈V 2)选择vj,使得D[j]=Min{D | vi∈V-S} 3)修改从v出发到集合V-S上任一顶点vk可达的最短路径长度。例如求基本的三个顶点之间的最短路径,C程序如下:
// Floyd.cpp : 定义控制台应用程序的入口点。
//
//#include "stdafx.h"
#include<iostream>
#include<vector>
using namespace std;
#define INF 99999 //表示不可到达
#define MAXSIZE 4 //表示图的结点数
//邻接矩阵存储图的信息
/*int map[MAXSIZE][MAXSIZE]={
{0,4,6,6,INF,INF,INF},
{INF,0,1,INF,7,INF,INF},
{INF,INF,0,INF,6,4,INF},
{INF,INF,2,0,INF,5,INF},
{INF,INF,INF,INF,0,INF,6},
{INF,INF,INF,INF,1,0,8},
{INF,INF,INF,INF,INF,INF,0}
};*/
int map[MAXSIZE][MAXSIZE]={
{0,5,INF,7},
{INF,0,4,2},
{3,3,0,2},
{INF,INF,1,0}
};
//弗洛伊德算法
void Floyd()
{
int path[MAXSIZE][MAXSIZE];//保存最短路径
int A[MAXSIZE][MAXSIZE];//a[j]表示当前顶点i到j的最短距离
//数据初始化
for(int i=0;i<MAXSIZE;i++)
{
for(int j=0;j<MAXSIZE;j++)
{
A[j]=map[j];
path[j]=-1;//初始化为-1
}
}
//这个扫描所有点,没有除去对角线和划去的行和列上面的点
/*for(int diagonal=0;diagonal<MAXSIZE;diagonal++)//左对角线
{
for(int k=0;k<MAXSIZE;k++)//行
{
for(int j=0;j<MAXSIZE;j++)//列
{
if(A[k][j]>A[k][diagonal]+A[diagonal][j])
{
A[k][j]=A[k][diagonal]+A[diagonal][j];
path[k][j]=diagonal;
}
}
}
}
*/
for(int diagonal=0;diagonal<MAXSIZE;diagonal++)//左对角线
{
for(int k=0;k<MAXSIZE;k++)//行
{
if(k!=diagonal)//除去此行所有的点
{
for(int j=0;j<MAXSIZE;j++)//列
{
if(j!=diagonal)//除去此列所以的点
{
if(k!=j)//除去对角线的点
{
if(A[k][j]>A[diagonal][j]+A[k][diagonal])//满足条件
{
A[k][j]=A[diagonal][j]+A[k][diagonal];
path[k][j]=diagonal;
}
}
}
}
}
}
}
//结果输出:
for(int i=0;i<MAXSIZE;i++)
{
for(int j=0;j<MAXSIZE;j++)
{
if(A[j]==INF)
cout<<"从顶点"<<i<<"到顶点"<<j<<"不存在路径"<<endl;
else
{
cout<<"从顶点"<<i<<"到顶点"<<j<<"最短距离为: "<<A[j]<<" 其路径为:";
vector<int>temp;
temp.insert(temp.begin(),j);//把终点插入
int ok1=i,ok2=j;
while(true)
{
ok1=path[ok1][ok2];
if(ok1==-1)
break;
temp.insert(temp.begin(),ok1);
}
temp.insert(temp.begin(),i);//把起点插入
for(int z=0;z<temp.size();z++)
cout<<temp[z]<<" ";
cout<<endl;
}
}
}
}
int main()
{
Floyd();
return 0;
}


