基础题目
超级基础的题
虽然是数学,但是仍以 \(OI\) 的题为例,毕竟 \(OI\) 的组合计数题还是很高质的,但别担心,组合计数主要是数学推导,所以文中的题仅会推导数学的理论知识或公式,不会有代码实现。但为了方便,还是会把题目链接放出来。
注:不是 \(OIer\) 的就不必在意题目的数据范围了,以及题里的取模也不用管
高中生就会
luogu P8557 炼金术(Alchemy)
题目描述
铃是一个爱玩游戏的女孩子。
她在游戏中想要炼制一种稀有合金 —— 这需要 n 种金属来合成。
她准备好矿石后建造了 k 个不同的熔炉,当熔炉启动时,会随机炼出这 n 种金属中的一些(也可能什么都没有)。
如果把每个熔炉炼出的金属收集起来,有了全部 n 种金属,就能造出合金了。澪对此很好奇,对铃说:「我考考你,有多少种情况可以炼出合金呢?」这个简单的问题铃很快就会做了,你能求出结果吗?
答案可能很大,请对 998244353 取模(即除以 998244353 的余数)后输出。
作者很懒,不想形式化题意了,相信聪明的你们有一定能看懂的
思路:
合法方案就是要求每种矿石至少在一个熔炉里被冶炼,那么,我们可以把 每个熔炉看成 元素,每种矿石看成一个集合,某种矿石在哪几个熔炉里冶炼,那么这个集合里就有哪几个元素,所以,我们只许让每个集合 非空,方案就是 合法 的,所以对于每种矿石,它的非空子集就有 \(2^k-1\) 种,\(n\) 种矿石就是 \(n\) 个 \(2^k-1\) 相乘,即 \((2^k-1)^n\) 种方案。
对 \(OIer\) 说:
代码实现直接敲个快速幂就好了,公式都给你了,不能不会了吧,记得取模!
luogu P3197 [HNOI2008] 越狱
题目描述
监狱有 n 个房间,每个房间关押一个犯人,有 m 种宗教,每个犯人会信仰其中一种。如果相邻房间的犯人的宗教相同,就可能发生越狱,求有多少种状态可能发生越狱。
答案对 100,003 取模。
思路:
正难则反:可能发生越狱的方案数 \(=\) 总方案数 \(-\) 不可能发生越狱的方案数
总方案数 很好求,每个房间都有 \(m\) 种宗教可以信仰,\(n\) 个房间就是 \(m^n\) 种方案数
不可能发生越狱的方案数:就是任意相邻的房间的信仰的宗教不同,其实只要保证,每一间房间都和前一间房间的信仰不同,就可以了:第 \(1\) 间房间可以信仰 \(m\) 种宗教;第 \(2\) 间为了跟第 \(1\) 间的信仰不同,只有 \(m-1\) 种宗教可以信仰;第 \(3\) 间只需跟第 \(2\) 间不同即可,也有 \(m-1\) 种宗教可以信仰;第 \(4,5,6...n\) 间,都有 \(m-1\) 种宗教可以信仰,根据 乘法原理,把 \(n\) 间房间的各可信仰数相乘即可:\(m(m-1)^{n-1}\)
所以答案是:\(m^n-m(m-1)^{n-1}\)
对 \(OIer\) 说:
依旧是快速幂加个取模就可以了
错排数:
介绍:
错排列问题是组合数学中的一个经典问题,指的是将n个元素重新排列,使得每个元素都不在原来的位置上。错排列数记为D(n),即n个元素的错排列数。这个问题最早由尼古拉·伯努利和欧拉研究,因此也称为伯努利-欧拉的装错信封问题。
人话就是,给了一个 \(n\),然后求 \(1\) ~ \(n\) 的所有排列里,每个数字和当前排列下其对应的下标不同的方案数。
\(eg.\) \(n=3:\)
\(2_1,3_2,1_3\)
\(3_1,1_2,2_3\)
就是错排列,右下角的数字就是下标,所以,\(D(3)=2\)
然后,不难发现,\(D(1)=0,D(2)=1,D(3)=2\),这是错排数的前几项
接着推导 \(D(n)\) 的递推式:
\(n\) 个数错排,我们先考虑其中一个数 \(a\),根据定义,这个数不能在其数值所对应的下标 \(a\) 上(就是如果是数字 \(2\),在这个排列里就不能放在下标为 \(2\) 的位置),那么,它可以去侵占其他 \(n-1\) 个数的位置
继续考虑,如果这个数 \(a\) 侵占了其他的 \(n-1\) 个数中的某个数 \(b\) 的位置,那么 \(b\) 可以放到哪里?
有两种选择:一种是反过来偷家,即把 \(b\) 放到 \(a\) 原本正确的位置(就是放到下标为 \(a\) 的位置上),方案数就是 \(D_{n-2}\)
另一种选择:\(b\) 去侵占另外的其他 \(n-2\) 个数的位置,方案数就是算上 \(b\) 的那 \(n-1\) 个数的错排数,为 \(D_{n-1}\)
所以,\(a\) 侵占其他 \(n-1\) 个数中的某一个数的位置的方案数就是 \(D_{n-1}+D_{n-2}\),有 \(n-1\) 个数可以选择侵占,所以 \(D_n=(n-1)(D_{n-1}+D_{n-2})\)
完美的递推式子,当然,还有一个直接计算公式:
这我就不想证了,感兴趣的话自己去看看吧,问题是这玩意的复杂度也是 \(O(n)\) 的,还不如线性递推,同样 \(O(n)\) 还能把 \(D_{1\sim n}\) 都求出来,不过,这玩意让我想到了一位故式:欧拉函数 \(\phi_n\) 的直接计算式:
\(\phi_n=n(1-\dfrac{1}{p_1})(1-\dfrac{1}{p_2})(1-\dfrac{1}{p_3})...(1-\dfrac{1}{p_k})\) 其中,\(p_i\) 为 \(n\) 的质因子
额,扯远了,这是数论里的,别来我们组合计数里凑热闹
好了,前置知识说完了,看题吧:
luogu P4071 [SDOI2016] 排列计数
题目描述
求有多少种 1 到 n 的排列 a,满足序列恰好有 m 个位置 i,使得 \(a_i=i\)。
答案对 \(10^9+7\) 取模。
思路:
就相当于,从 \(n\) 个数里先选 \(m\) 个数,让它们的位置正确,然后剩下 \(n-m\) 个数错排就好了,从 \(n\) 个数里选 \(m\) 个数,有 \(C_{n}^{m}\) 种选择,每种对应的方案数都是剩下 \(n-m\) 个数的错排数 :\(D_{n-m}\)
所以答案:
可能会有人说了:\(C_{n}^{m}\) 我还能算,但是 \(D_{n-m}\) 是个什么鬼,但是,别忘了,这是 \(OI\) 题,我们是可以用计算机递推出 \(D_{n-m}\) 的,所以我们就表示成这样了
对 \(OIer\) 说:
本题每个测试样例有 \(T(T\le 5e5)\) 组数据,且 \(1\le n\le1e6\),\(0\le m\le 1e6\),得 \(O(n)\) 预处理 \(1\sim n\) 的阶乘并 \(O(nlogM)\) 处理其逆元(其中 \(M\) 是模数 \(1e9+7\)),还有 \(O(n)\) 处理错排数 \(D_{1\sim n}\)
Catalan 数
介绍:
卡特兰数(Catalan数)是组合数学中一个常见的数列,通常用于解决各种计数问题。其定义为:第 \(n\) 个卡特兰数 \(C_n\) 可以通过公式计算:\(C_n = \dfrac{(2n)!}{n!(n + 1)!}\)。卡特兰数的前几项为\(1, 1, 2, 5, 14, 42, 132, 429, 1430\)等。它们在许多领域中有实际应用,包括出栈次序、括号序列等问题。
好了,这是我从网上粘来的,看不看吧,直接从例题里看:
luogu P1044 [NOIP 2003 普及组] 栈
相信就算不是 \(OIer\) 应该也见过这种题(反正我初二的时候有次数竞卷子上就有这选择题),很经典的 \(Calatan\) 数
题目背景
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作,即 pop(从栈顶弹出一个元素)和 push(将一个元素进栈)。
栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而他自己无法给出答案,所以需要你的帮忙。
题目描述
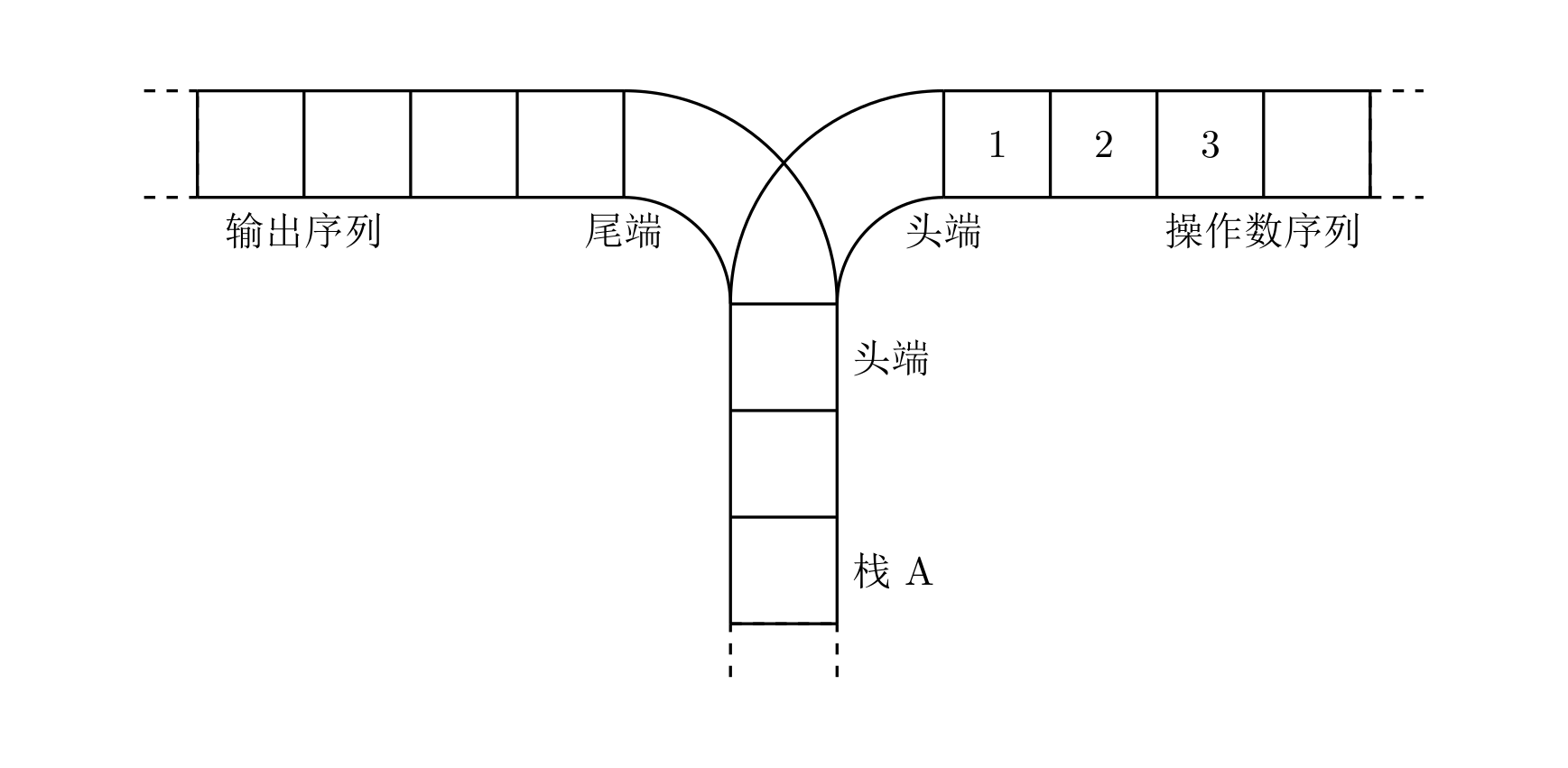
宁宁考虑的是这样一个问题:一个操作数序列,1,2,…,n(图示为 1 到 3 的情况),栈 A 的深度大于 n。
现在可以进行两种操作,
将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的 push 操作)
将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的 pop 操作)
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列,下图所示为由 1 2 3 生成序列 2 3 1 的过程。
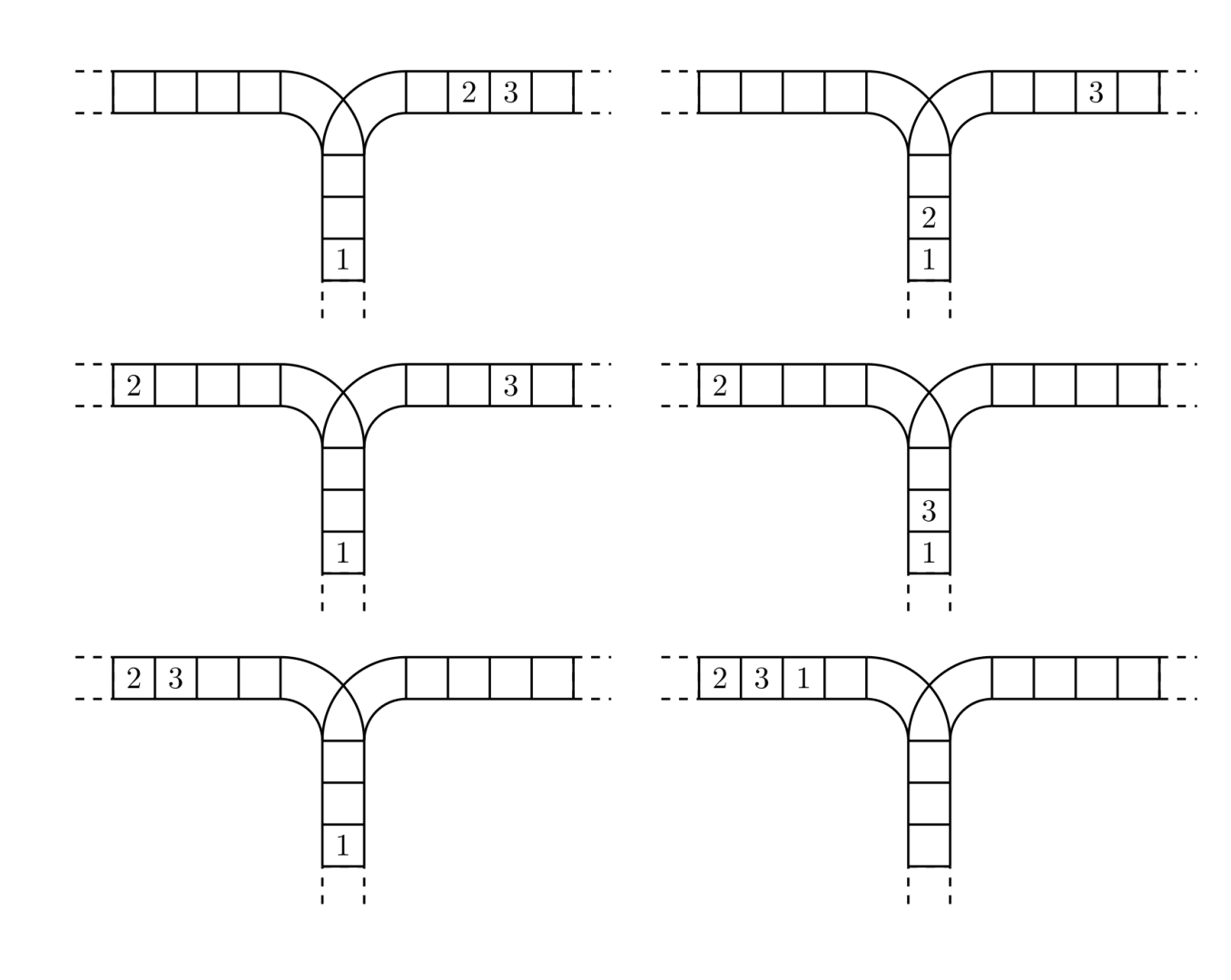
原始状态如上图所示)
你的程序将对给定的 n,计算并输出由操作数序列 1,2,…,n 经过操作可能得到的输出序列的总数。
直接把洛谷的原题粘过来了,以这道题为例,介绍 \(Catalan\) 数:
这里转换一下,我们把 入栈 记为 \(+1\),出栈 记为 \(-1\),所以一种合法的操作序列就要求:该序列的任意前缀和都不小于零
\(eg.\) 当 \(n=3\) 时,合法的操作序列是:
\(+1,+1,+1,-1,-1,-1\)
\(+1,+1,-1,+1,-1,-1\)
\(+1,+1,-1,-1,+1,-1\)
\(+1,-1,+1,+1,-1,-1\)
\(+1,-1,+1,-1,+1,-1\)
如果有一个序列是:\(+1,+1,-1,-1,-1,+1\)
那么就是非法的,因为下标为 \(5\)(下标从 \(1\) 开始)时,前缀和为:\(+1+1-1-1-1=-1 < 0\)
带入本题实际意义就是:先连续入栈了 \(2\) 个元素,但又要连续出栈 \(3\) 个元素,不难发现出栈之前,栈里的元素不够 \(3\) 个,所以没办法再连续出栈第 \(3\) 个元素,然后序列就非法了
接着是几何意义:
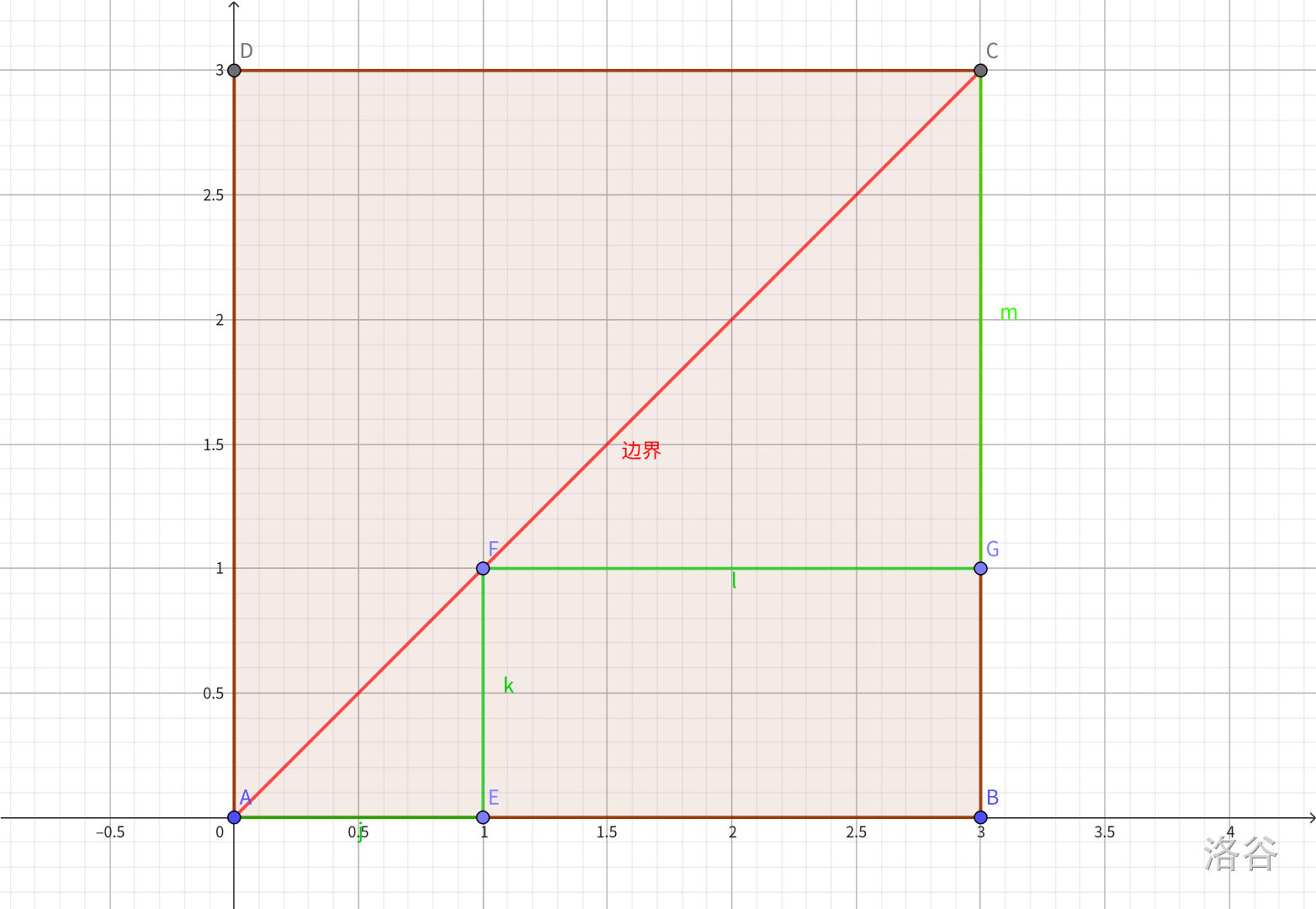
我们以 \((0,0)\) 为起点,操作序列中每出现一个 \(+1\),就向 右移动一个单位,每出现一个 \(-1\),就 向上移动一个单位。所以,一种合法操作序列就要求:无论何时,点都不能移动到超过 \(y=x\) 这条对角线的位置
仍以 \(n=3\) 为例,就是要求从 \((0,0)\) 移动到 \((3,3)\) 这个点且不会有超过对角线部分 的路径数,图中的绿色路径就是一种合法的,它所对应的操作序列是:\(+1,-1,-1,+1,+1,-1\)
而下面这个图中的蓝色路径就对应了一种不合法的序列:\(+1,+1,-1,-1,-1,+1\)
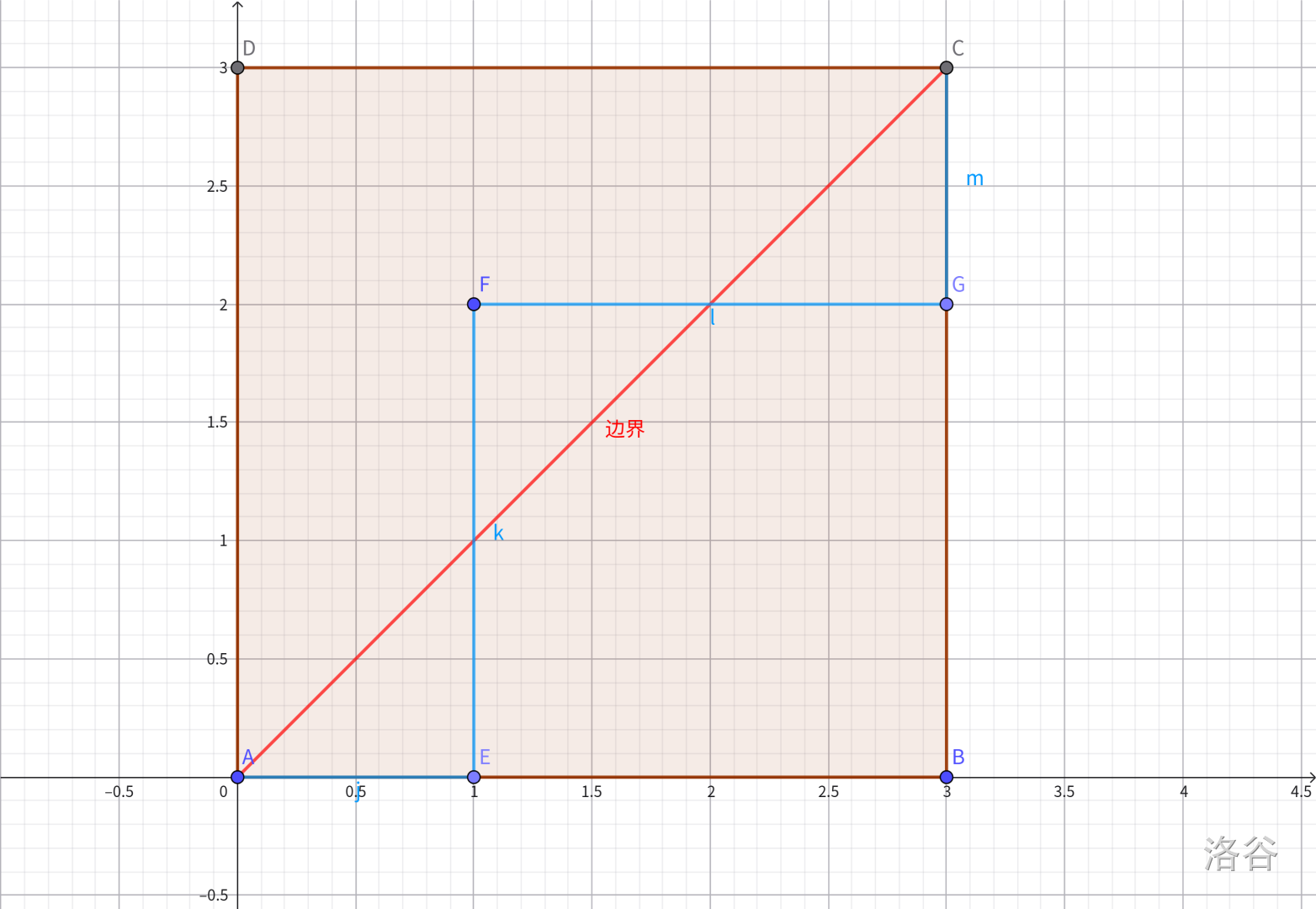
从这个图里,我们知道了,只要路径有一段超过边界就不合法,哪怕它后来回到了边界一下,上图中点 \(F\) 就已经超过了边界,就算到点 \(G\) 时,回到了边界之下,也是不合法的
好了,这就是几何意义,详细的例子还有:
好了,介绍完基础问题了,接着说怎么做:
先求出 总路径数:就是从 \(n\) 个 \(+1\) 和 \(n\) 个 \(-1\) ,一共 \(2n\) 个数里选 \(n\) 个位置放 \(+1\)(或者选 \(n\) 个位置放 \(-1\)),所以有 \(C_{2n}^{n}\) 种总方案数
接着,不合法的方案数:
这里有很巧妙的转换法,以图辅助理解:
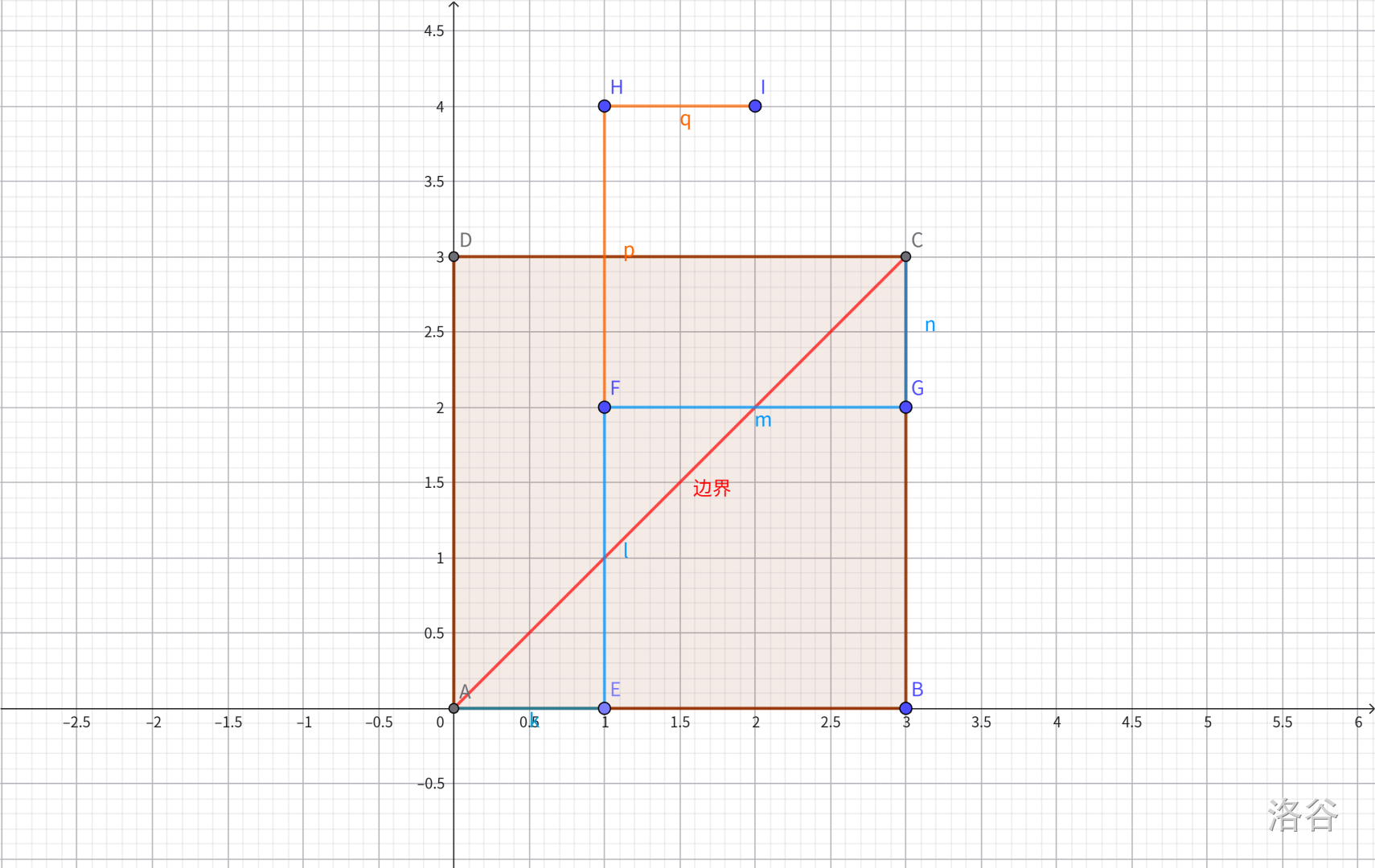
图中,蓝色路径是原路径,可以看出来是不合法的,此时,我们把超出边界以上的第一个点(即 \(F\))之后的路径(即 \(FG-GC\))对称到上面,即橙色部分(即 \(FH-HI\)),然后,我们发现,此时新的路径的终点变成了 \((n-1,n+1)\)。事实上,所有不合法的路径对可以由对称变换为起点为 \((0,0)\),终点为 \((n-1,n+1)\) 的一条路径,且数量就是从 \((0,0)\) 到 \((n-1,n+1)\) 的路径数,所以为 \(C_{2n}^{n+1}\)(当然也可以是 \(C_{2n}^{n-1}\),由组合数的性质,这两个是相等的)
所以最后的答案即为:\(C_{2n}^{n}-C_{2n}^{n+1}\)
这就是 \(Catalan\) 数第 \(n\) 项的公式,即 \(Cat_n=C_{2n}^{n}-C_{2n}^{n+1}\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号