B-Tree

B-Tree

B-Tree 引出

B-Tree 是用于访问磁盘文件的数据结构，没错，学习 B-Tree 就是为了深入了解数据库的

1，AVL树 和 红黑树效率已经非常高了，难道不适合访问磁盘数据吗？
是的，因为 B-Tree 是 多叉树，二叉树一个节点最多两个子节点，B-Tree 一个节点多个节点，所以层高会更小

2，为什么层高小的更适合做磁盘数据的访问？
数据是保存在节点上的，要访问到节点才能得到数据，每次访问节点就是一次 I/O，如果数据在内存就发生内存 I/O ，如果数据在磁盘就发生磁盘 I/O
磁盘的访问速度比内存慢 10⁵~10⁶ 倍，所以访问磁盘数据尽量上发生 I/O，层高越小肯定 I/O 就越少

3，二叉树和多叉树层高具体差多少？多叉树必然比二叉树层级低，低多少呢
100w 数据使用二叉树的数据结构，层高大约是20 log2(1000000) ≈19.93
100w 数据使用多叉树（每个节点允许多少个子节点是关键，B-Tree 500 很常见），层高大约是 3 log500(1000000)≈2.223 向上取整

度、阶

度：degree，节点的子节点数量

阶：order，所有节点中子节点最多的数量

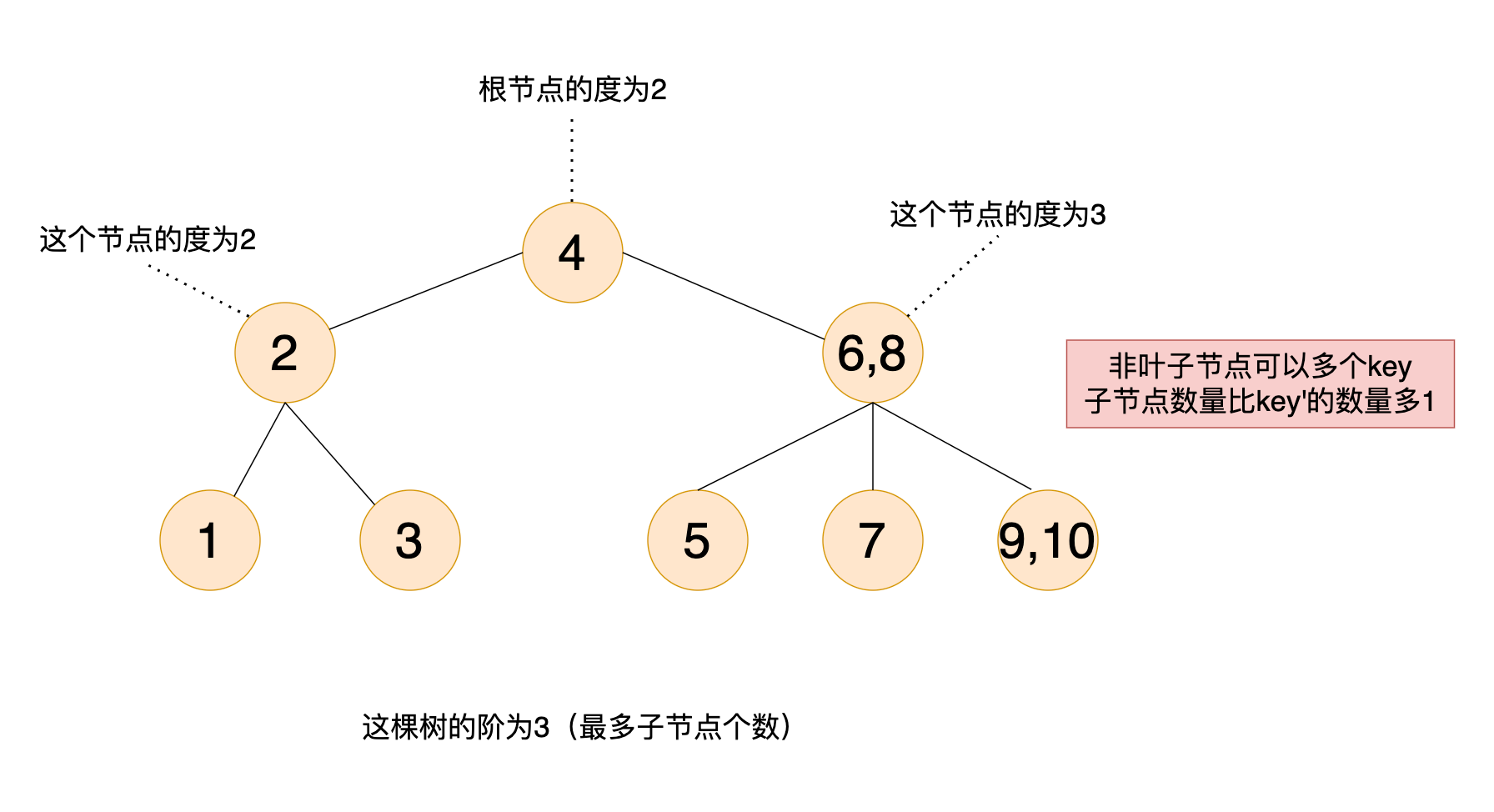
B-Tree 的特性

1. 每个节点最多有 m 个子节点，m 就是 B-Tree 的阶
2. 除根节点和叶子结点外，其他其他每个节点至少有 m/2 个子节点（向上取整，限制节点数量的下限）
3. 若根节点不是叶子节点，则根节点至少有两个子节点
4. 所有叶子节点都在同一层（限制叶子节点的高度，保证查询到叶子节点的时间复杂度不要差的太大）
5. 每个非叶子节点由 【n 个 key】 和 【n+1 个子节点】 组成，n 需满足 (m/2 - 1) <= n <= (m-1)（限制 key 的数量）
   • 子节点比 key 多一个（key 比子节点少一个）
   • 第一个特性规定子节点数量最大是 m，第二个特性规定子节点数量最小为 m/2
   • 所以推导出公式 (m/2 - 1) <= n <= (m-1)
6. 所有的 key 升序排列（为什么 MySql 不设置ID也会自动生成一个隐藏的整形的ID就是这个原因，要满足数据结构的规则）
   • 每一层是升序（从左到右看）
   • 左子结点的 key < 当前节点的 key < 右子节点的 key

为什么 key 的数量比子节点数量少1？

带着数据实际来分析更容易理解，比如上面的图中，6-8 这个节点，子节点是 5、7、9-10，要找大于 4 的 key，有以下场景：

1. 如果要查 5 这个 key，6-8 是没有的，所以要到子节点中找，因为 5 小于 6，所以找小于 6 的子节点
2. 如果要找 7 这个 key，6-8 也没有，也要到到子节点中找，7 介于 6 - 8 之间，所以不会找小于 6 的子节点，也不会找大于8的子节点
3. 如果要找 10 这个 key，6-8 也没有，也要到到子节点中找，10 是大于 8 的，所以找到的节点是 9-10 这个节点，在这个节点继续找到 10

B-Tree 非叶子节点存放数据吗？

答案是 不存放，全网误传

1. MySql 压根用的就不是 B-Tree 而是 B+Tree：前提都不成立，为什么还说 B-Tree 非叶子节点也存放数据呢
2. B-Tree 的数据结构特性：也没说存放数据，明确的是 key 和 下级节点指针
3. 《MySQL 技术内幕：InnoDB 存储引擎》：InnoDB 使用 B+Tree 索引，所有数据记录都存储在叶子节点中
4. 《算法导论》（第3版）：B-Tree 的内部节点仅包含键和子节点指针，不存储卫星数据
5. MySQL 官方文档：InnoDB 索引是 B+Tree 结构，非叶子节点仅用于导航

极少数数据库（如 MongoDB 的 WiredTiger）在 B-Tree 基础上允许非叶子节点缓存数据，但这 非常规设计

多路查找

这就是普通的多叉树查找，专业术语

二叉树查找一次排除一颗子树（一条分支），多叉树一次可排除多条分支

还有个特性也是因为是多叉树，层高比二叉树低，所以是矮胖结构，路径短

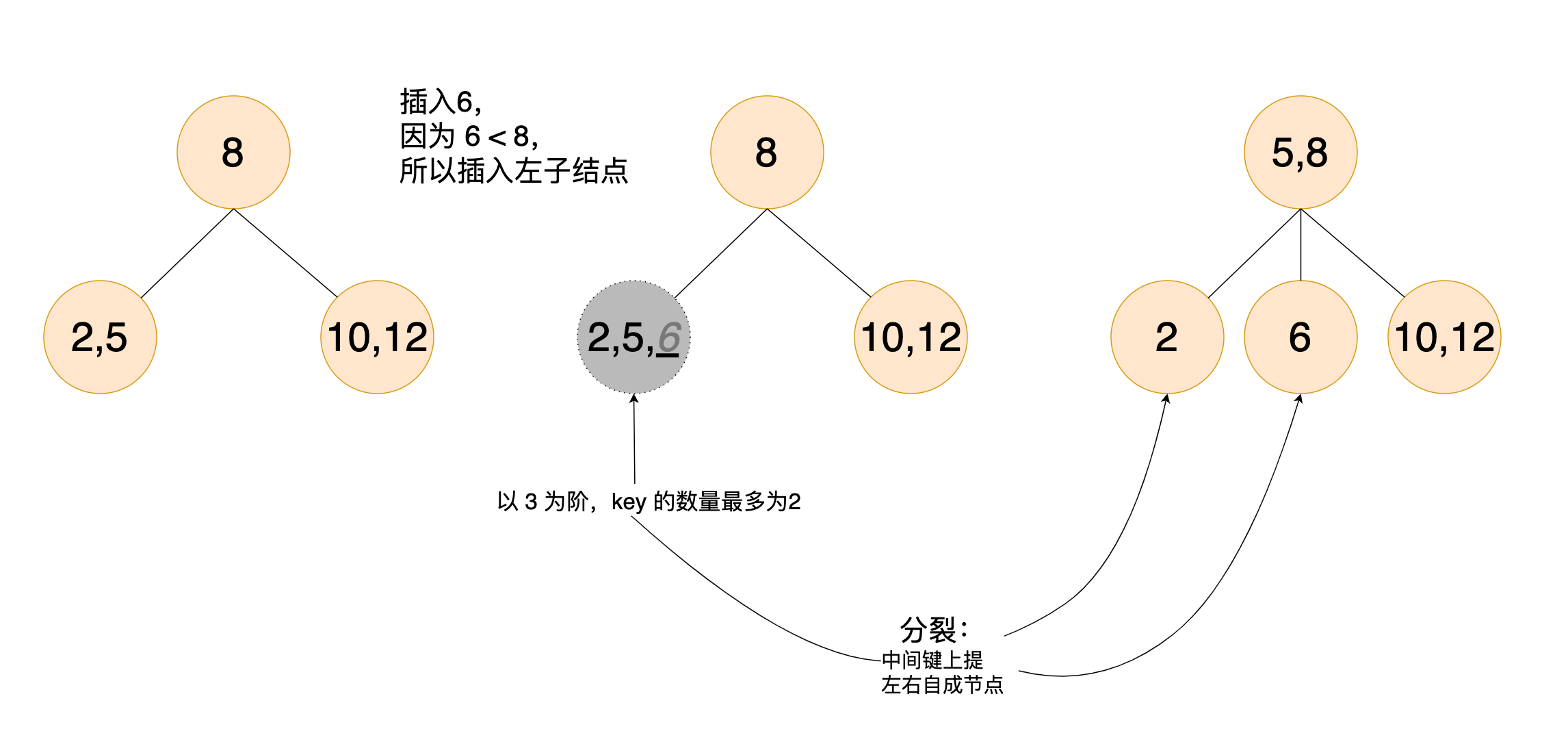
分裂

触发条件：对于一棵 m 阶 B-Tree，每个节点最多存储 m-1 个键。当插入新键后，节点键数达到 m，则必须分裂

分裂过程：中间键上提（m/2 向上取整来定位）、中间键左右拆分为两个键。如果根节点分裂就会增加层高

分裂的作用：
维持平衡：每个节点的 key 始终保持 ⌈m/2⌉-1 ≤ n ≤ m-1
控制树高：结果是横向扩展，而非增加层高（基本到不了根节点分裂，磁盘的阶会比较大）