AVL树

AVL树

AVL树概念

AVL树是最早发明的自平衡二叉搜索树，由Adelson-Velsky和Landis在1962年提出。它在普通二叉搜索树的基础上增加了平衡条件，确保树的高度始终保持在O(log n)级别。

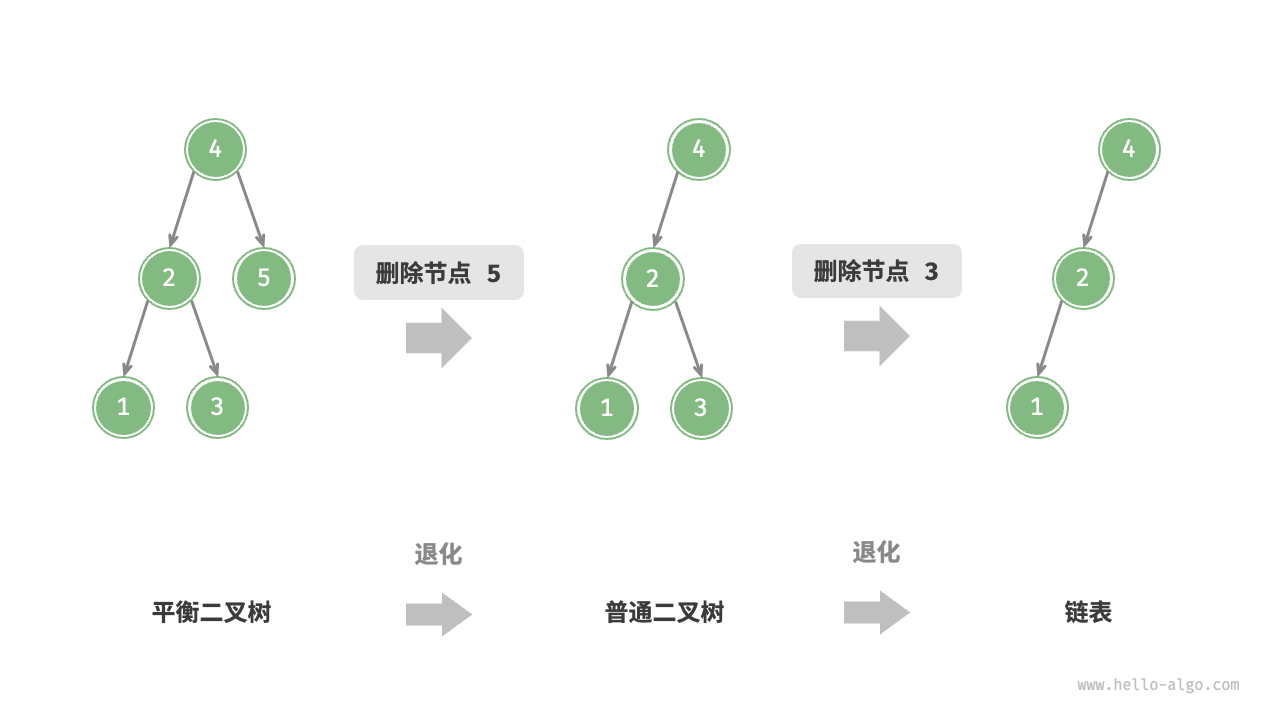
为什么会有 AVL 树？因为二叉搜索树极端情况下可能退化为链表，AVL 树就是使用保持树结构是平衡的（不平衡时就旋转，所以旋转是核心内容）

核心特性

1. 平衡因子：每个节点的平衡因子=左子树高度-右子树高度
2. 平衡条件：所有节点的平衡因子必须为-1、0或1
3. 旋转操作：当插入或删除破坏平衡时，通过旋转恢复平衡

上面是术语，说人话就是当 任一节点左右子树高度差大于1时就要旋转

判断失衡节点

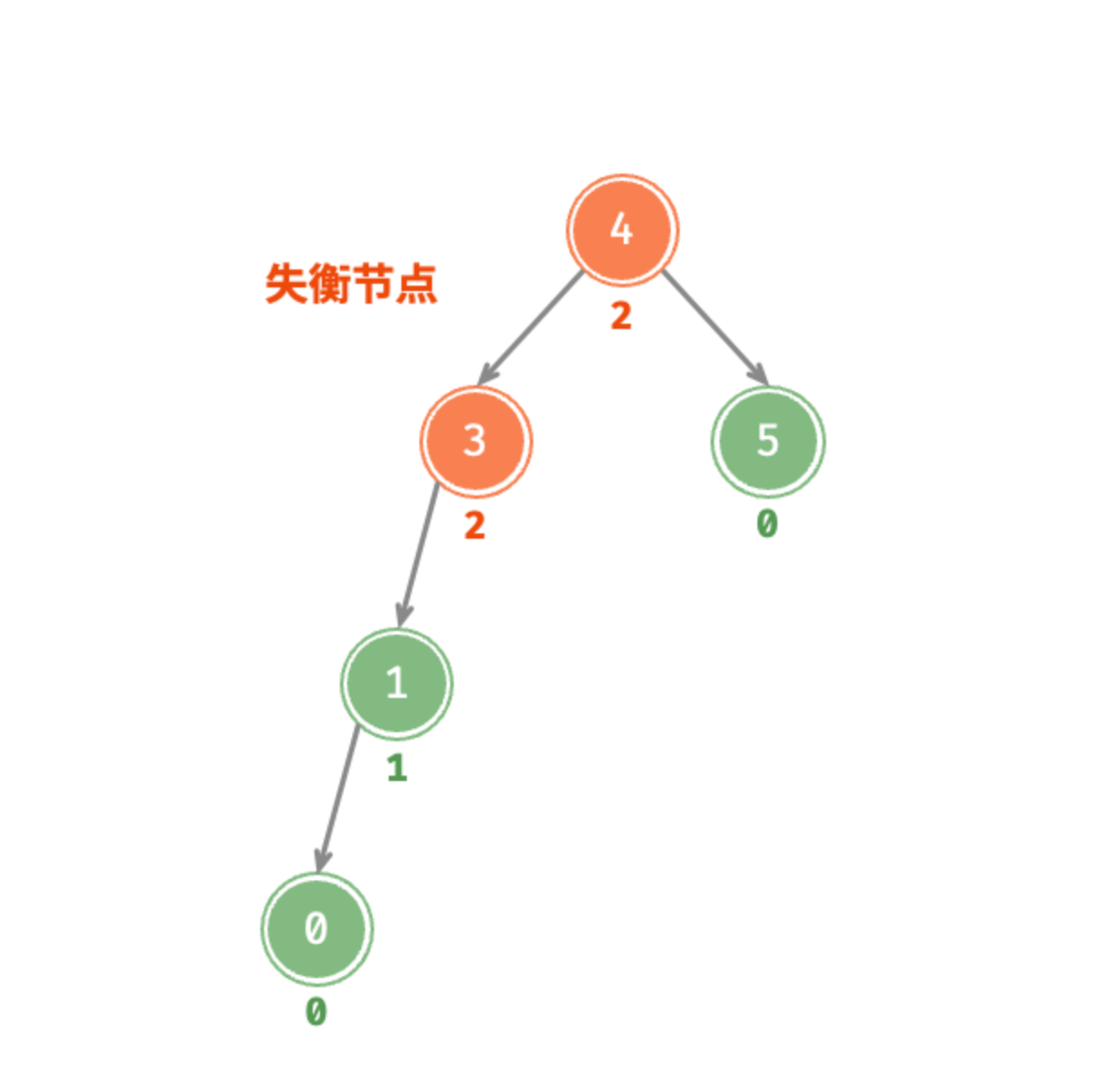
当某个节点的左右子节点的高度差大于1时，这个节点就是失衡节点，如下图 3 和 4 就是失衡节点，平衡因子都是 2

PS：实际编码中每个节点会维护一个 height 属性表示当前节点的高度

初窥旋转

先看看旋转就是是什么，旋转了后树会变成什么样，有个直观的印象

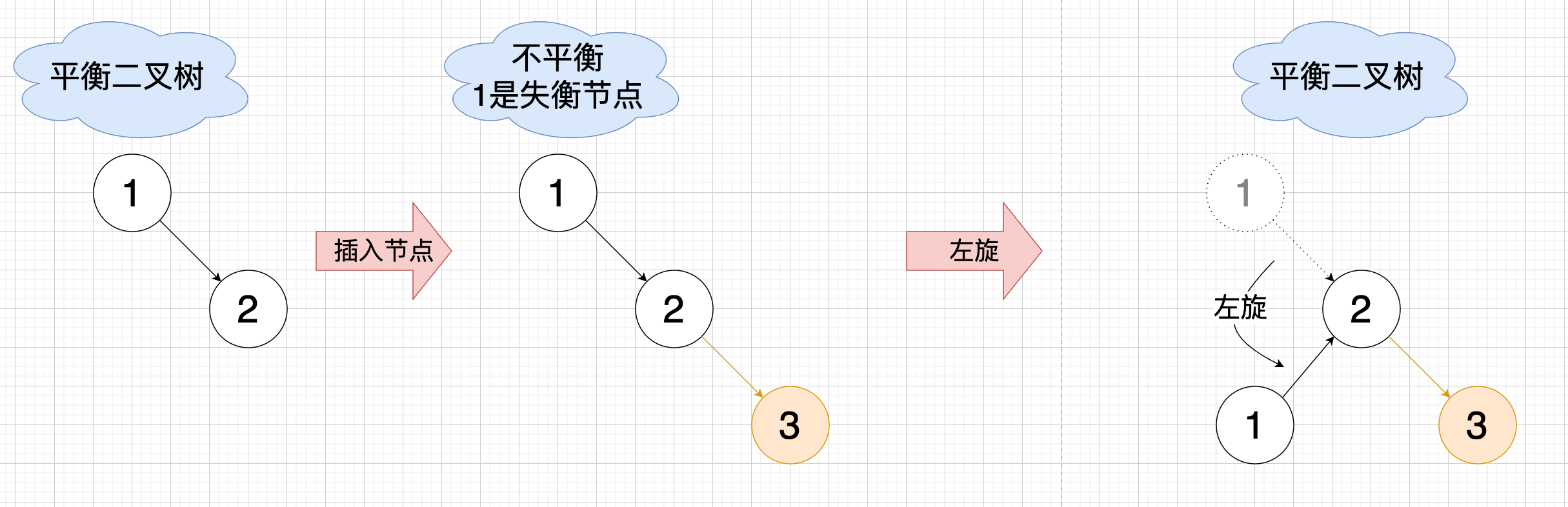
如下图在插入节点3 后， 节点1的右子树高3，左子树高是1，不平衡了，因为平衡因子是 2，并且是一颗右偏树，此时需要左旋

再探旋转

右偏树一定左旋吗？或者左偏一定右旋吗？答案是否定的，要根据失衡类型来决定旋转方式

某个节点失衡，看其两个子节点的高度差来决定旋转方式

失衡类型	描述	旋转方式
LL	左子树的左子树过高	单次右旋
RR	右子树的右子树过高	单次左旋
LR	左子树的右子树过高	先左旋后右旋
RL	右子树的左子树过高	先右旋后左旋

RR失衡：左旋

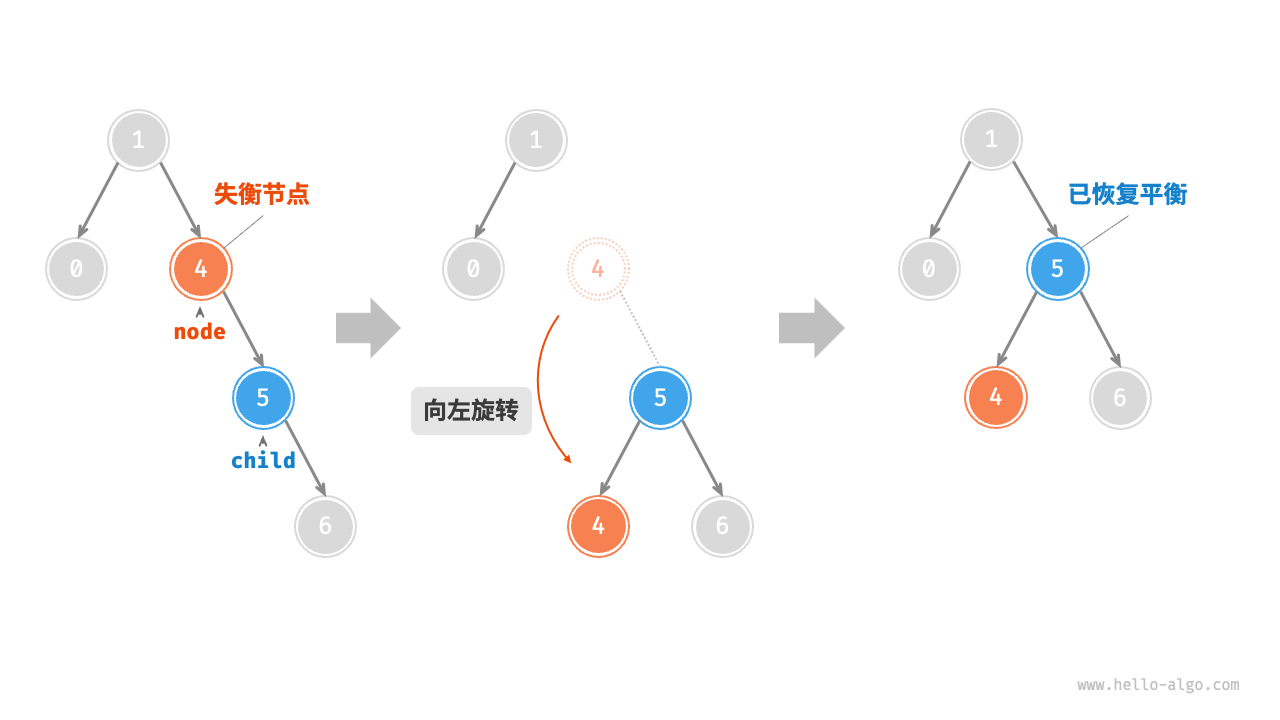
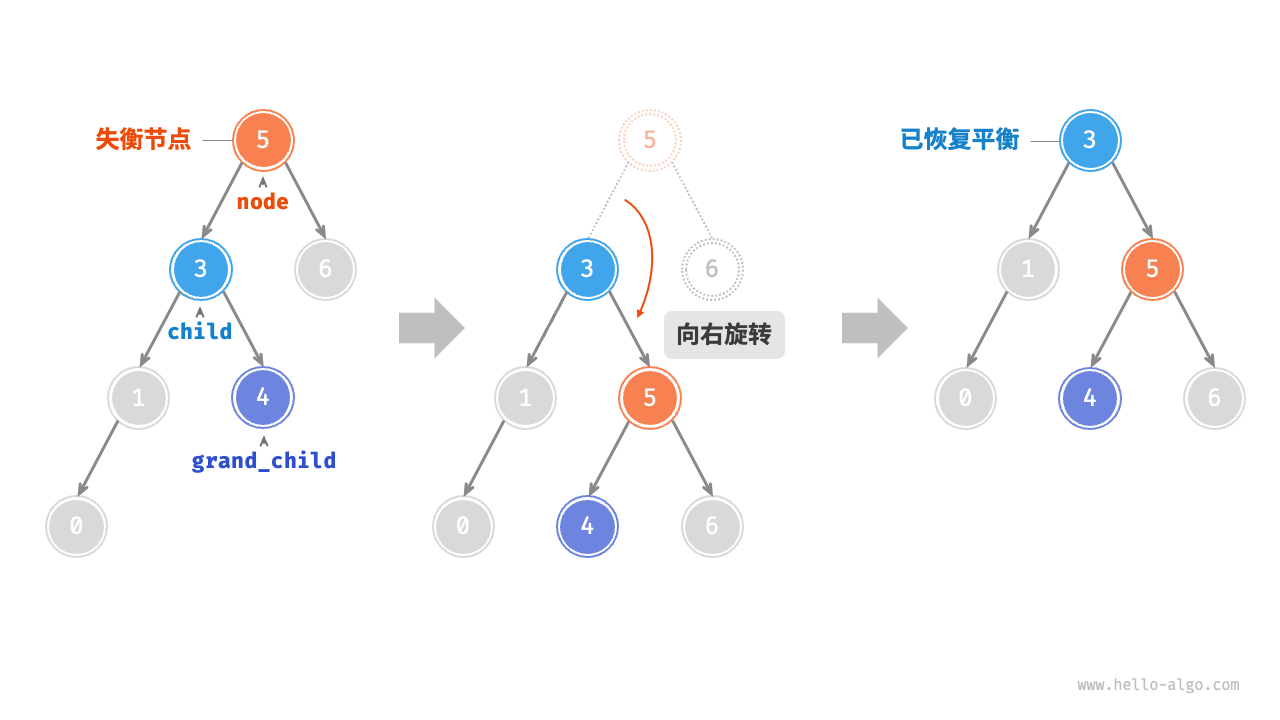
LL 失衡：右旋

RL 失衡：先右旋再左旋

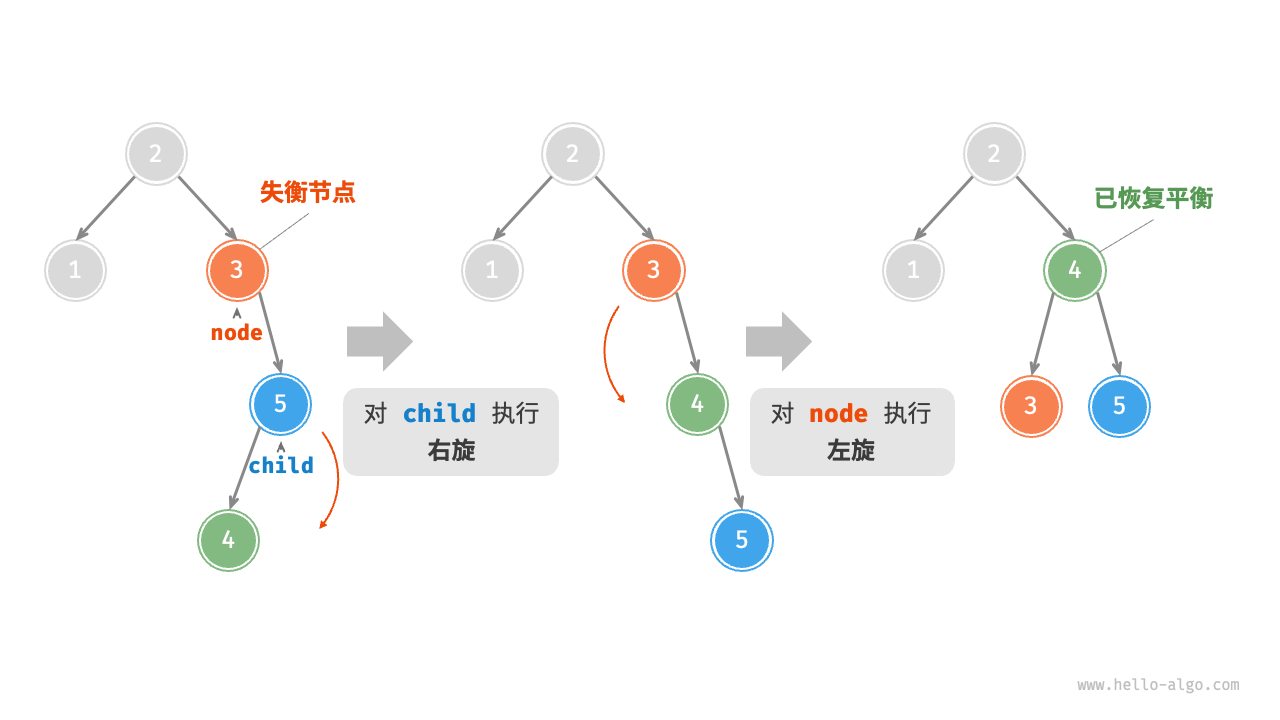
LR 失衡：先左旋再右旋

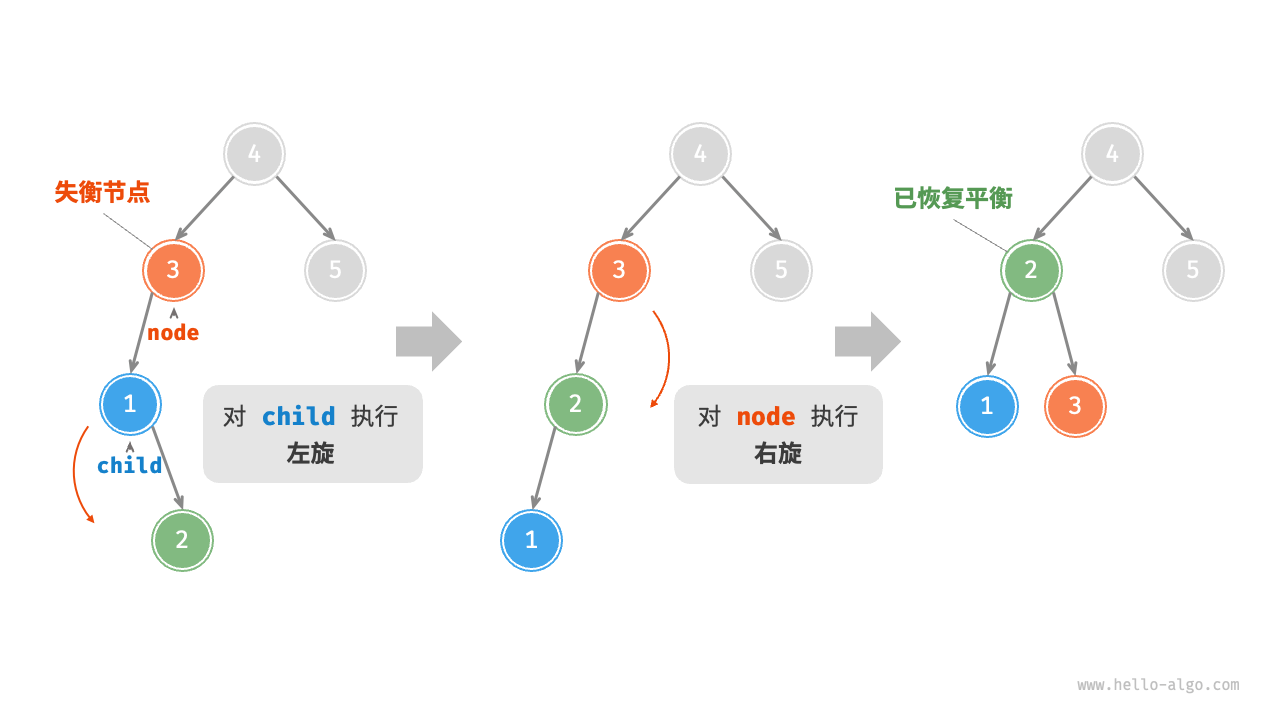
A -> B -> C：假设 B 失衡并且是单旋场景，以 B 的子节点（C）作为原点来旋转，旋转后 B 作为 C 的子节点，A 作为 C 的父节点

代码实现

class AVLNode {
    int key;
    int height;      // 节点高度（每个节点保存他的高度，快速判断是否需要旋转）
    AVLNode left;    // 左子节点
    AVLNode right;   // 右子节点

    public AVLNode(int key) {
        this.key = key;
        this.height = 1; // 新节点初始高度为1
    }
}

public class AVLTree {
    private AVLNode root;

    // 获取节点高度（处理null情况）
    private int height(AVLNode node) {
        return node == null ? 0 : node.height;
    }

    // 更新节点高度（当前节点高度 = 左右子树高度取高的再+1）
    private void updateHeight(AVLNode node) {
        node.height = 1 + Math.max(height(node.left), height(node.right));
    }

    // 获取平衡因子（左右子树高度差，不能取绝对值和1比较，因为后面要配合别的情况决定向哪个方向旋转）
    private int getBalance(AVLNode node) {
        // >1 表示左边太高；< -1 表示右边太高（0，1，-1 就是平衡的）
        return node == null ? 0 : height(node.left) - height(node.right);
    }

    // 右旋转（处理LL情况）
    private AVLNode rightRotate(AVLNode y) {
        AVLNode x = y.left;
        AVLNode T2 = x.right;

        // 执行旋转
        x.right = y;
        y.left = T2;

        // 更新高度（必须先更新y，再更新x）
        updateHeight(y);
        updateHeight(x);

        return x; // 返回新的根节点
    }

    // 左旋转（处理RR情况）
    private AVLNode leftRotate(AVLNode x) {
        AVLNode y = x.right;
        AVLNode T2 = y.left;

        // 执行旋转
        y.left = x;
        x.right = T2;

        // 更新高度
        updateHeight(x);
        updateHeight(y);

        return y; // 返回新的根节点
    }

    // 插入节点
    public void insert(int key) {
        root = insert(root, key);  // key 插入 root，返回表示
    }

    private AVLNode insert(AVLNode node, int key) {
        // 1. 执行标准BST插入（左子树所有节点 < 当前节点 < 右子树所有节点）
        if (node == null) {
            return new AVLNode(key);
        }

        if (key < node.key) {  // 当前节点如果小于根节点，说明要插入到左子树
            node.left = insert(node.left, key);  // 传入左子结点，递归
        } else if (key > node.key) {  // 插入到右子树
            node.right = insert(node.right, key);  // 传入右子结点，递归
        } else {
            return node; // 既不大于也不小于，就说明重复了
        }

        // 2. 更新节点高度
        updateHeight(node);

        // 3. 获取平衡因子检查是否平衡
        int balance = getBalance(node);

        // 4. 处理不平衡情况（4种case）

        // Case 1: LL（左左）
        if (balance > 1 && key < node.left.key) {
            return rightRotate(node);
        }

        // Case 2: RR（右右）
        if (balance < -1 && key > node.right.key) {
            return leftRotate(node);
        }

        // Case 3: LR（左右）
        if (balance > 1 && key > node.left.key) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }

        // Case 4: RL（右左）
        if (balance < -1 && key < node.right.key) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }

        return node; // 已经平衡则直接返回
    }

    // 中序遍历（验证树是否有序）
    public void inorder() {
        inorder(root);
    }

    private void inorder(AVLNode node) {
        if (node != null) {
            inorder(node.left);
            System.out.print(node.key + " ");
            inorder(node.right);
        }
    }

    // 测试代码
    public static void main(String[] args) {
        AVLTree tree = new AVLTree();

        // 插入测试数据
        tree.insert(10);
        tree.insert(20);
        tree.insert(30); // 会触发旋转
        tree.insert(40);
        tree.insert(50);
        tree.insert(25); // 会触发LR旋转

        // 中序遍历输出：10 20 25 30 40 50
        System.out.println("中序遍历结果:");
        tree.inorder();
    }
}

插入元素流程

1. BST标准插入（插入后可能不平衡，先不管，先把数据添加进去）

• 操作：按照二叉搜索树规则找到插入位置

• 动作：

  • 若当前节点为空，创建新节点并返回
  • 若插入值 < 当前节点值，递归进入左子树
  • 若插入值 > 当前节点值，递归进入右子树
  • 若值已存在，直接返回（假设不允许重复）

• 示例：

  if (node == null) return new AVLNode(key);
  if (key < node.key) {
      node.left = insert(node.left, key);
  } else if (key > node.key) {
      node.right = insert(node.right, key);
  }
  

2. 更新当前节点高度

• 操作：重新计算当前节点的高度

• 公式：height = 1 + max(左子树高, 右子树高)

• 代码：

  node.height = 1 + Math.max(height(node.left), height(node.right));
  

3. 平衡性检查（第一步插入时没处理平衡，这里来处理）

• 操作：计算当前节点的平衡因子

• 公式：平衡因子 = 左子树高 - 右子树高

• 检查：

  • 平衡因子 > 1：左子树更高（可能LL或LR型失衡）
  • 平衡因子 < -1：右子树更高（可能RR或RL型失衡）

• 代码：

  int balance = getBalance(node); // height(left) - height(right)
  

4. 失衡判断与旋转（如果不平衡，判断失衡类型，并旋转）

• 操作：根据失衡类型执行对应旋转

失衡类型	判断条件	旋转方式	具体动作
LL型	balance > 1 && key < node.left.key	单次右旋	当前节点的左子节点上升为新的根节点
RR型	balance < -1 && key > node.right.key	单次左旋	当前节点的右子节点上升为新的根节点
LR型	balance > 1 && key > node.left.key	先左旋后右旋	1. 对左子节点左旋 2. 对当前节点右旋
RL型	balance < -1 && key < node.right.key	先右旋后左旋	1. 对右子节点右旋 2. 对当前节点左旋

5. 返回调整后的节点

• 操作：返回当前子树的根节点

• 注意：

  • 若发生旋转，返回旋转后的新根节点
  • 若未失衡，直接返回原节点

• 代码：

  return rotatedNode; // 或 return node（未旋转时）
  

时间复杂度

操作	时间复杂度
查找	O(log n)
插入	O(log n)
删除	O(log n)
旋转	O(1)