堆（Heap）

堆（Heap）数据结构

堆是一种特殊的完全二叉树，它满足堆属性（Heap Property），在计算机科学中有广泛应用，特别是优先队列、堆排序等场景。

核心特性

• 完全二叉树结构：1 除最后一层外，其他节点完全填满；2 最后一层节点从左到右连续排列
• 堆属性：
  • 小顶堆：每个节点的值都小于或等于其子节点的值（根节点最小）
  • 大顶堆：每个节点的值都大于或等于其子节点的值（根节点最大）

堆的结构

最常见的是数组实现，结构如下：

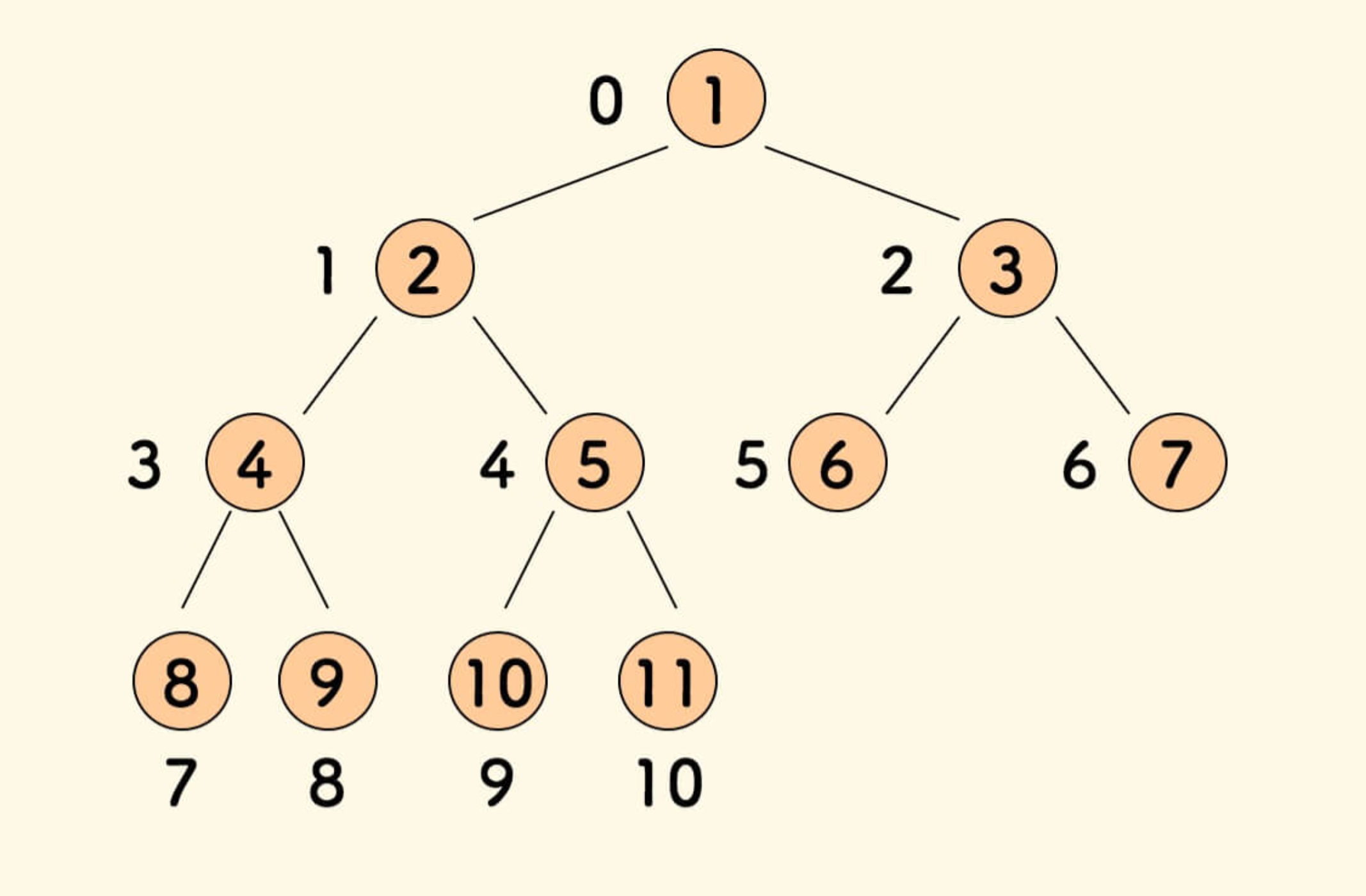
结合数组的直观示意图如下：

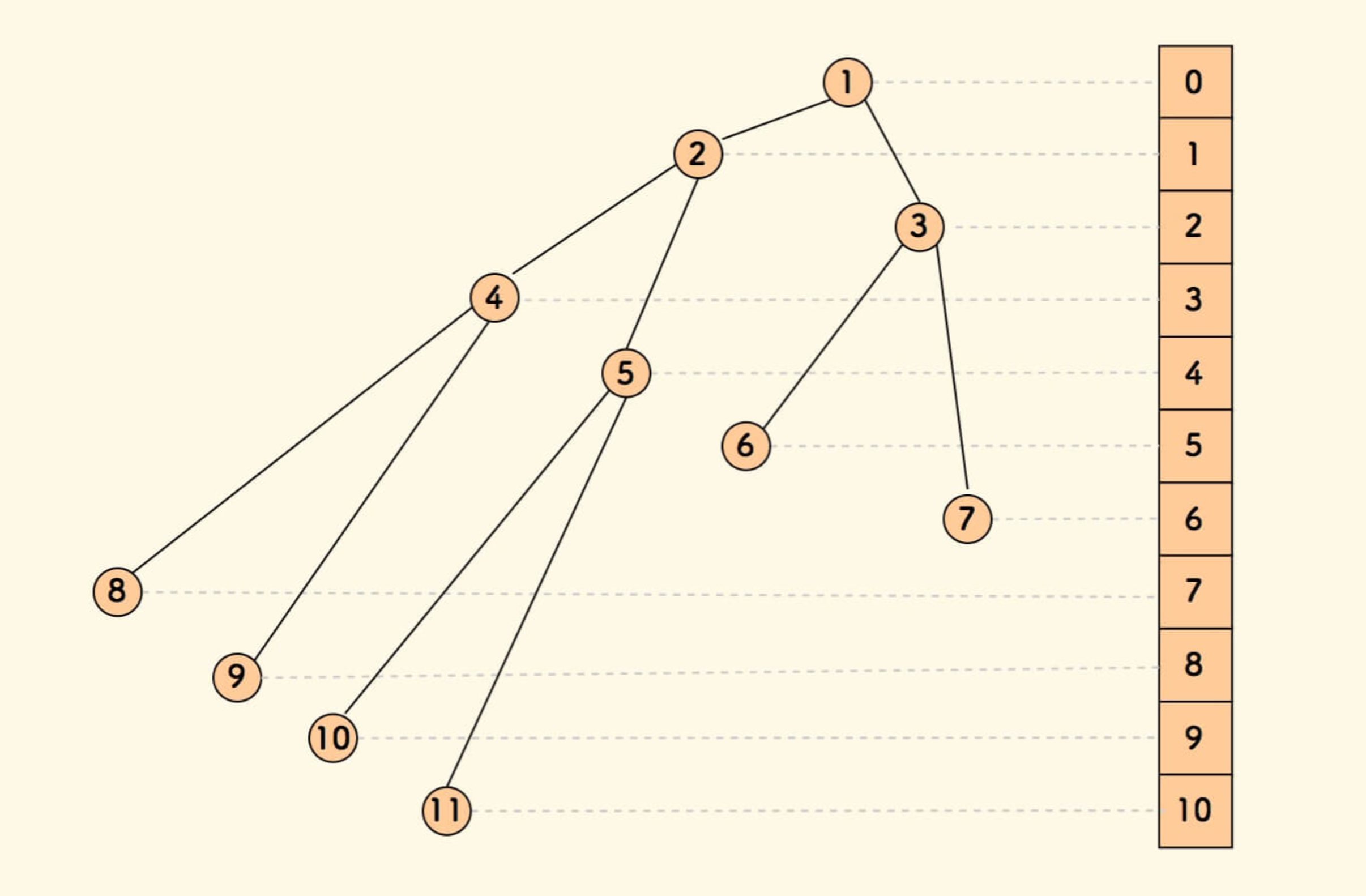
数组实现的堆，某个节点的父子节点下标的规律，如果当前节点的下标是 i，那么父节点和子节点：

• 父节点：父节点 = (i-1)/2（向下取整，java 默认行为，如果是别的语言要处理一下）
• 左子节点：左孩子 = 2*i + 1
• 右子节点：右孩子 = 2*i + 2

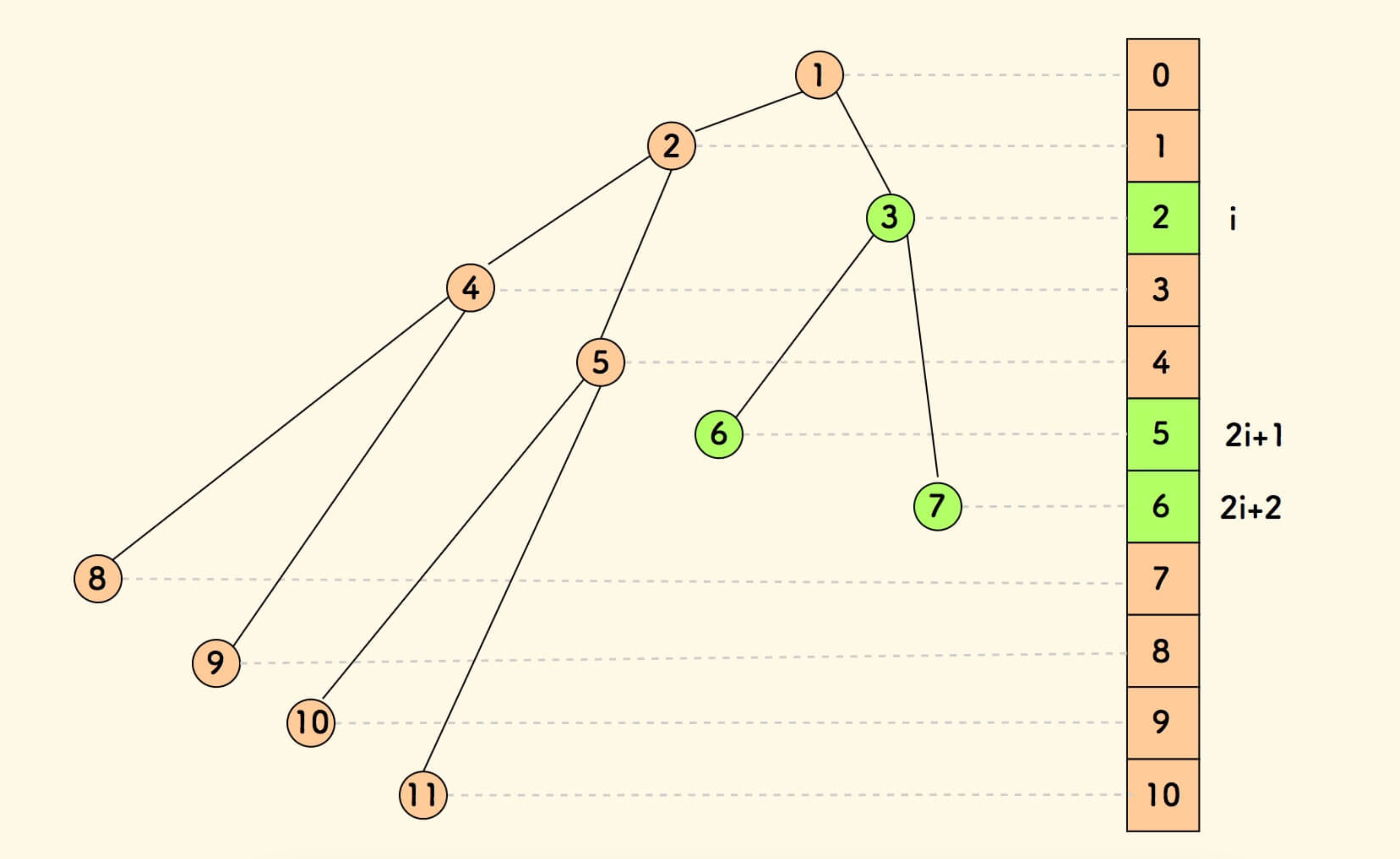
如果数组不从0开始，父节点： i / 2，左子结点： 2*i，右子节点：2*i+1

代码实现

小顶堆，数组下标从1开始

public class MinHeap {
    private final int[] heap;
    private int size;
    private final int capacity;

    // 构造函数
    public MinHeap(int capacity) {
        this.capacity = capacity;
        this.size = 0;
        this.heap = new int[capacity + 1]; // 索引0不使用，从1开始
    }

    // 获取父节点索引
    private int parent(int pos) {
        return pos / 2;
    }

    // 获取左子节点索引
    private int leftChild(int pos) {
        return 2 * pos;
    }

    // 获取右子节点索引
    private int rightChild(int pos) {
        return 2 * pos + 1;
    }

    // 交换两个节点
    private void swap(int fpos, int spos) {
        int tmp = heap[fpos];
        heap[fpos] = heap[spos];
        heap[spos] = tmp;
    }

    // 判断是否是叶子节点
    private boolean isLeaf(int pos) {
        return pos > (size / 2) && pos <= size;
    }

    // 下潜（核心方法）
    private void heapifyDown(int pos) {

        // 如果是叶子结点没必要下潜了
        if (!isLeaf(pos)) {

            // 先找到当前节点的两个子节点的下标
            int left = leftChild(pos);
            int right = rightChild(pos);

            // 假设当前节点是最小
            int smallest = pos;

            // 当前节点和左子结点比较，如果子节点大，不用交换位置。left <= size 为了避免越界，left = 2*i。更完善的做法是扩容
            if (left <= size && heap[left] < heap[smallest]) {
                smallest = left;
            }

            // 当前节点和有子节点比较
            if (right <= size && heap[right] < heap[smallest]) {
                smallest = right;
            }

            // 比较完后能知道[当前节点]、[左子节点]、[右子节点] 哪个最小，如果当前节点不是最小的，要交换位置
            if (smallest != pos) {
                swap(pos, smallest);  // 交换位置
                heapifyDown(smallest); // 递归下潜
            }
        }
    }

    // 上浮（核心方法）
    private void heapifyUp(int pos) {
        // 下标大于1才需要上浮，因为 =1 时已经是根节点了。并且当前节点大于父节点才需要上浮。两者都满足时就停止循环
        while (pos > 1 && heap[pos] < heap[parent(pos)]) {  // 使用循环而不是递归，下潜用的递归
            swap(pos, parent(pos));  // 交换当前节点和父节点
            pos = parent(pos);  // 每次遍历更新 pos，下次循环使用。也是指定循环截止条件
        }
    }

    // 插入元素
    public void insert(int element) {
        if (size >= capacity) {
            throw new IllegalStateException("Heap is full");
        }
        heap[++size] = element;
        heapifyUp(size);
    }

    // 移除并返回最小元素
    public int extractMin() {
        if (size == 0) {
            throw new IllegalStateException("Heap is empty");
        }
        int popped = heap[1];
        heap[1] = heap[size--];
        heapifyDown(1);
        return popped;
    }

    // 获取最小元素但不移除
    public int peek() {
        if (size == 0) {
            throw new IllegalStateException("Heap is empty");
        }
        return heap[1];
    }

    // 测试
    public static void main(String[] args) {
        MinHeap minHeap = new MinHeap(15);
        minHeap.insert(5);
        minHeap.insert(3);
        minHeap.insert(17);
        minHeap.insert(10);
        minHeap.insert(84);
        minHeap.insert(19);
        minHeap.insert(6);
        minHeap.insert(22);
        minHeap.insert(9);

        System.out.println("The Min val is " + minHeap.extractMin());
        System.out.println("The Min val is " + minHeap.extractMin());
    }
}

时间复杂度

操作	时间复杂度	说明
插入（Insert）	O(log n)	添加到末尾并向上调整
删除根节点（Extract）	O(log n)	移除根节点，将最后一个元素移到根部并向下调整
查看根节点（Peek）	O(1)	直接返回根节点值
构建堆（Heapify）	O(n)	从最后一个非叶子节点开始向下调整

写在最后

堆虽然单独拿出来讲，确实也应该单独拎出来，因为堆比较特别，数据结构是数组是线性的，但是逻辑上又是非线性（二叉树）
同时这玩意也是队列！优先队列，最优先的就是根节点，优先级依次往下
所以 JDK 中有已经实现好的堆，也就是各个优先队列

PriorityQueue 小顶堆实现（根节点最小，根节点就是最优先的），线程不安全
PriorityBlockingQueue 小顶堆实现（根节点最小，根节点就是最优先的），线程安全