二叉树（Binary Tree）

二叉树（Binary Tree）

图片来于 hello 算法

什么是二叉树？

• 线性数据结构下一个元素是一个，树的下一个节点是多个，二叉树的下一个节点最多两个，逻辑存储上是非线性的

• 存储结构可以是线性（简单的树）也可以是非线性（复杂的树）

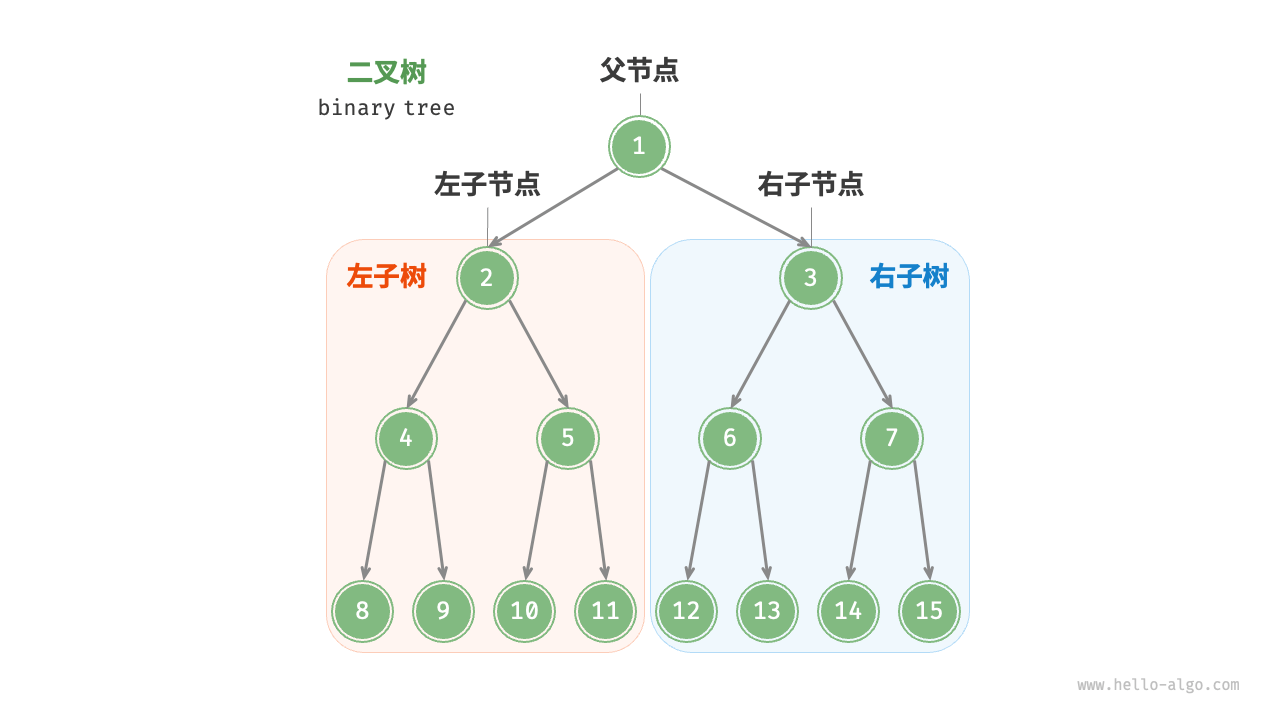
常见术语

• 根节点（root node）：顶层节点，没有父节点。

• 叶子节点（leaf node）：没有子节点的节点，其两个指针均指向 null 。

• 节点所在的层（level）：从顶至底递增，根节点所在层为 1 。

• 节点的度（degree）：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。

• 二叉树的高度（height）：根节点到深度最大的叶子节点的层级数量。

• 节点的深度（depth）：根节点到当前节点的层级数量。

• 节点的高度（height）：当前节点到其深度最大的子节点的层级数量。

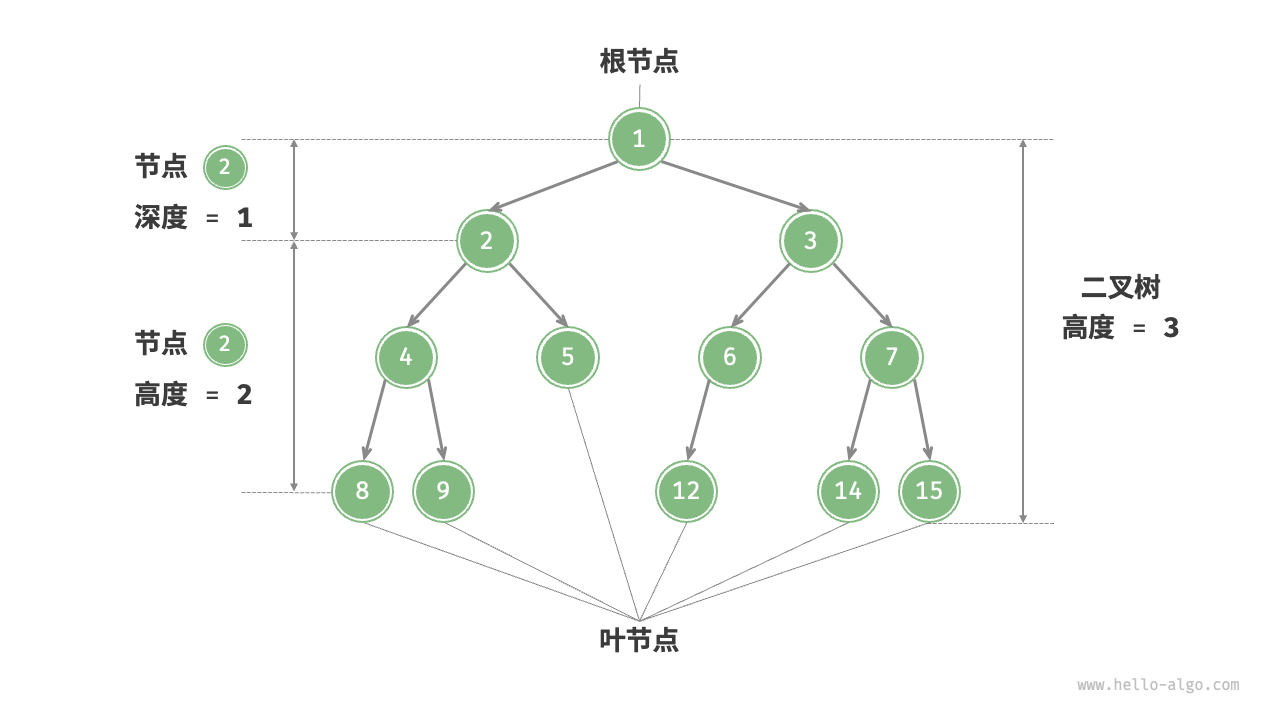
二叉树遍历

分为深度（Depth-First Search）和广度（Breadth-First Search）两种遍历方式
深度就是竖向遍历（父节点到叶子节点），广度就是横向遍历（一层一层来遍历，同辈分先遍历然后是下一辈分）

深度优先遍历（DFS）又分为三种方式：

1. 前序遍历（根-左-右）
2. 中序遍历（左-根-右）
3. 后序遍历（左-右-根）

广度和深度对比

特性	BFS	DFS
数据结构	队列（Queue）	栈（Stack）
空间复杂度	O(最宽层的节点数)	O(树的高度)
最短路径	✅ 天然支持	❌ 需额外处理
实现方式	迭代	递归/迭代
适用场景	层级遍历、最短路径问题	全路径遍历、回溯问题

二叉树分类

完美二叉树

所有的节点被填满，元素无序

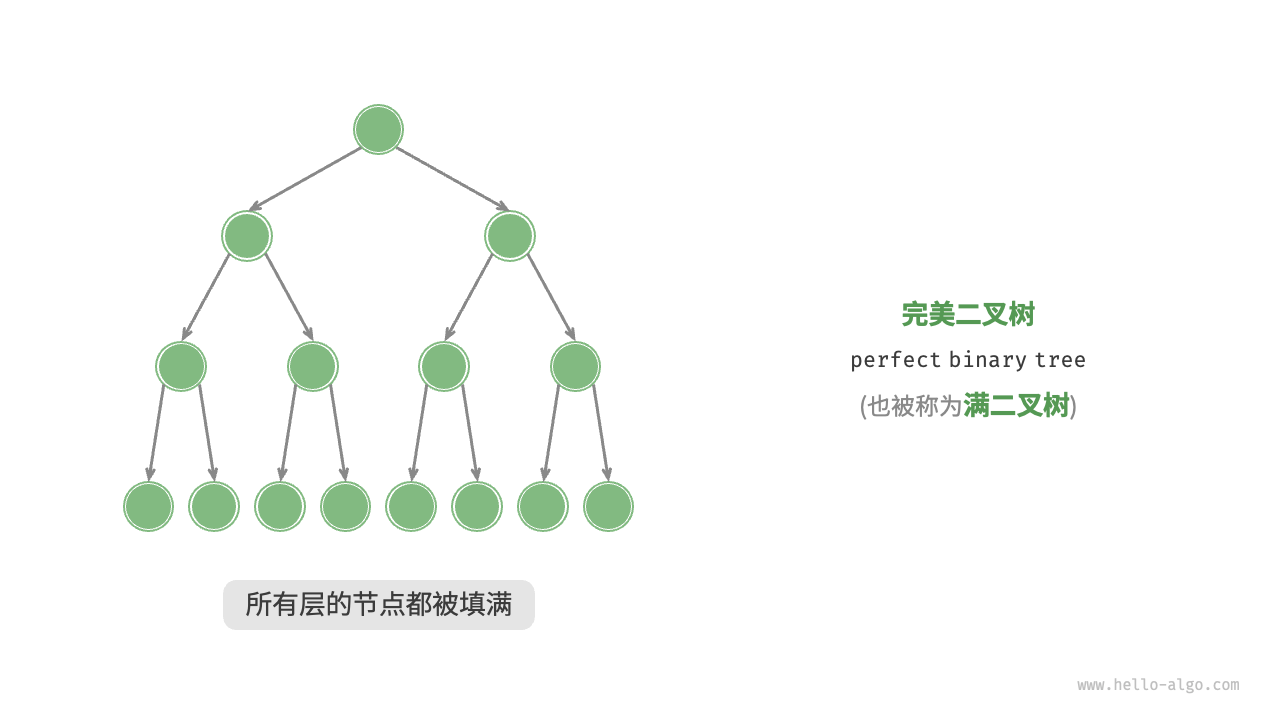
完全二叉树

除最后一层外，其他节点完全填满；最后一层节点从左到右连续排列，元素无序

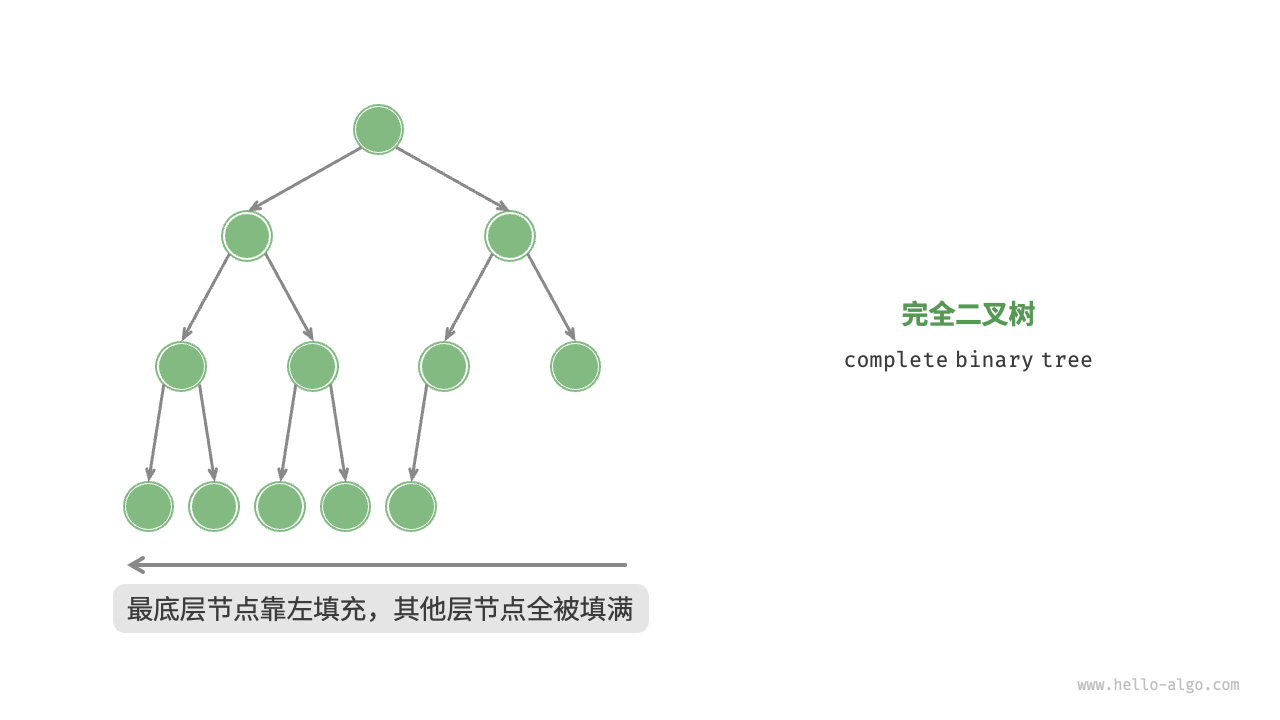
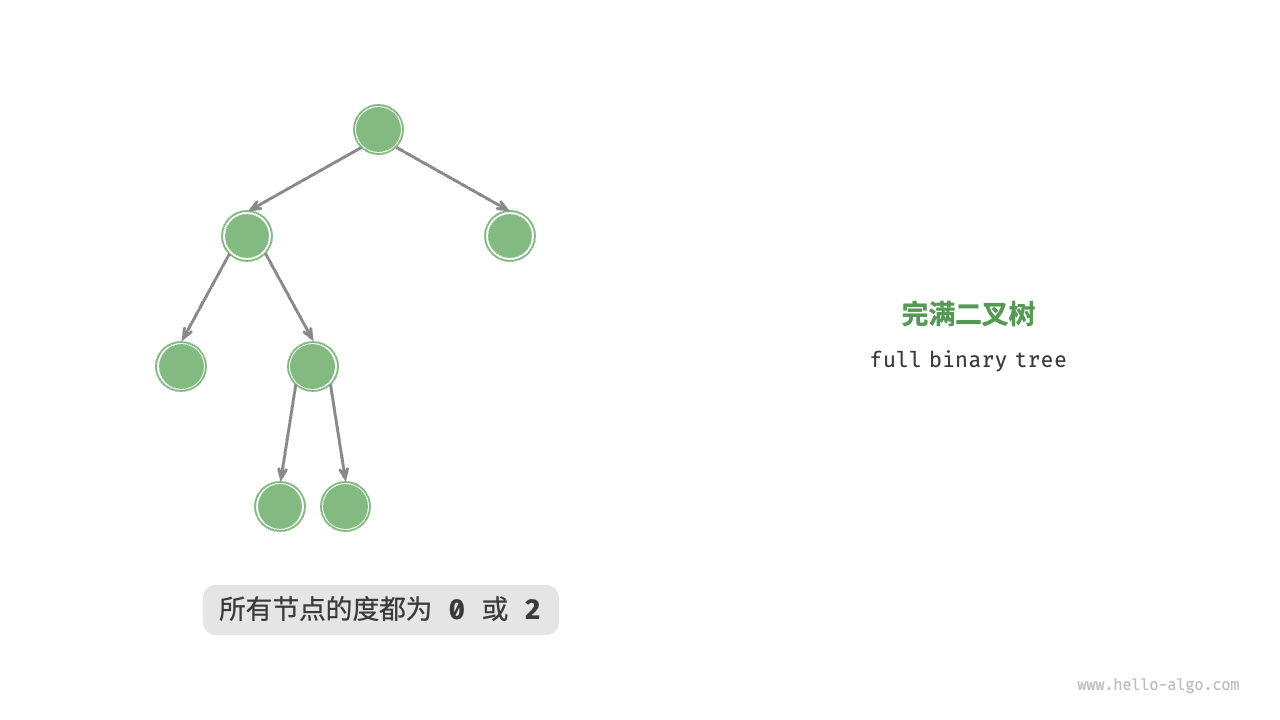
完满二叉树

所有的节点的子节点数量为 0 或 2，不能是1，元素无序

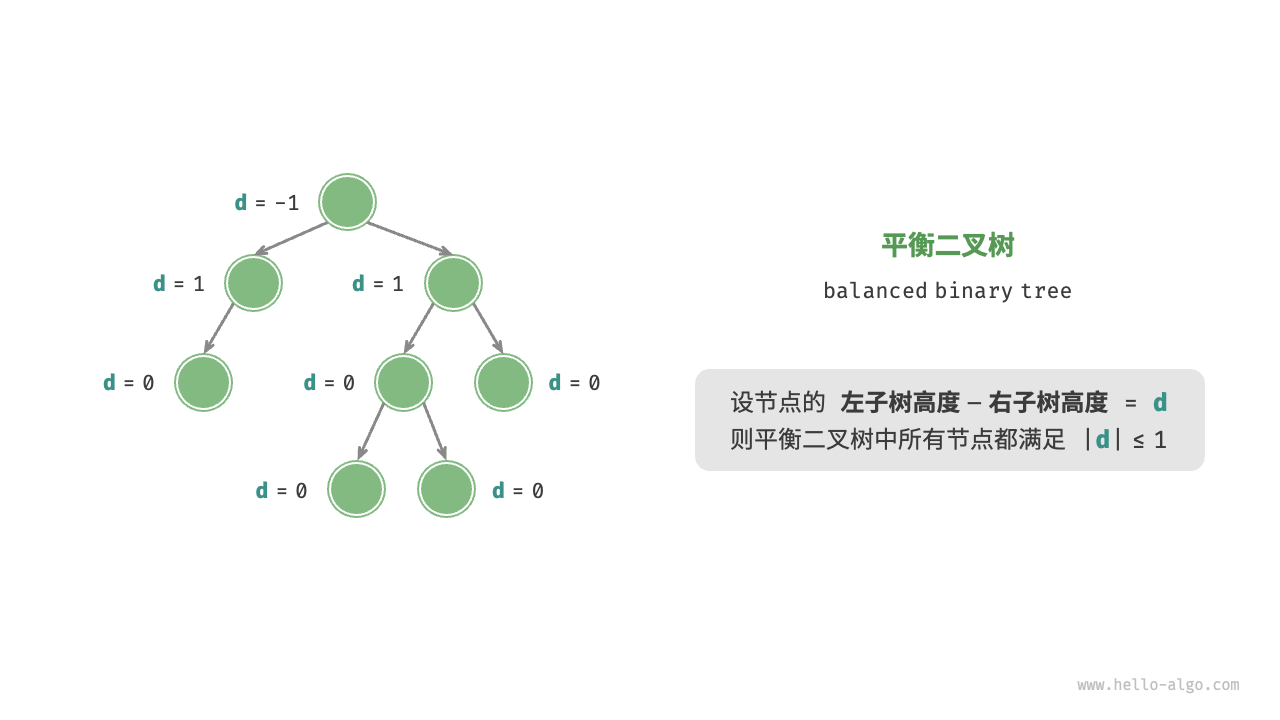
平衡二叉树

对于任一节点来说，左右子树高度差不能大于 1，元素无序

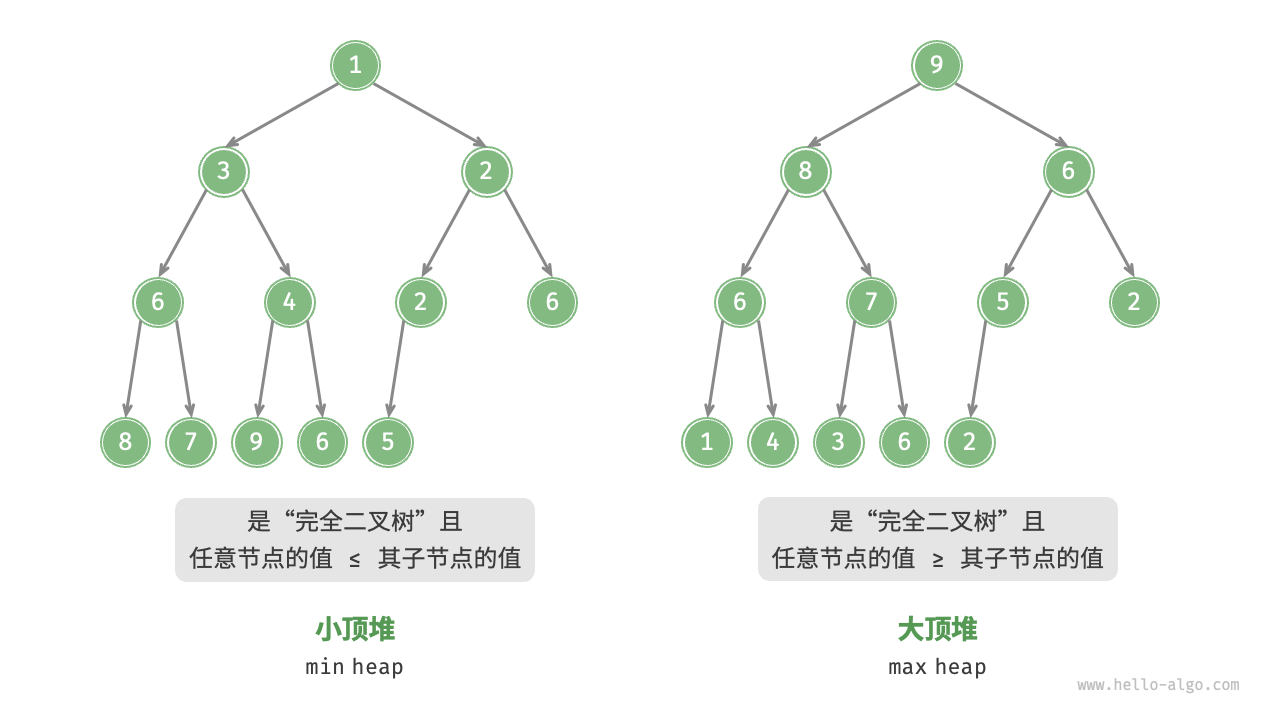
堆

堆既是完全二叉树，也是平衡二叉树，元素有序（只要元素有序就保证了时间复杂度不会太大，就有用武之地了~）
符合完全二叉树：1 除最后一层外，其他节点完全填满；2 最后一层节点从左到右连续排列
符合平衡二叉树：对于任一节点来说，左右子树高度差不能大于 1

堆自己的特性：元素有序。父节点的值 >= 所有子节点的值（大顶堆，根节点最大）或父节点的值 <= 所有子节点的值（小顶堆，根节点最小）

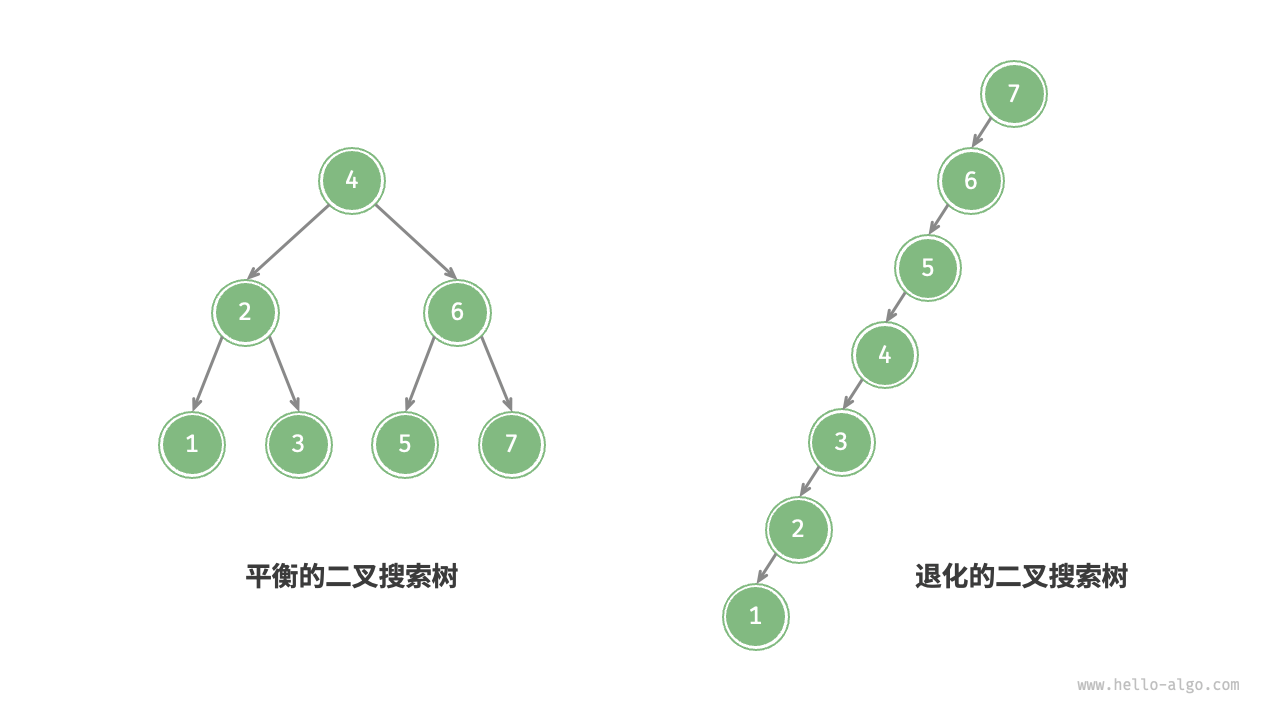
二叉搜索树

既然是搜索树，肯定要有顺序 但不要求平衡

任一节点都需要满足：左子树所有节点的值 < 当前节点的值 < 右子树所有节点的值

PS：堆 VS 二叉搜索树

特性	堆（Heap）	二叉搜索树（BST）
顺序	父节点 ≥（或 ≤）子节点（可以是两个方法）	左子树 < 根节点 < 右子树（只能一个方向）
结构	完全二叉树 + 平衡二叉树	任意二叉树（最差可能退化成链表）
平衡性	平衡	完全看运气是否平衡（ AVL 和红黑树是平衡的）
主要用途	快速访问/删除极值（如最大/最小值）	动态维护有序数据，支持高效查找

大顶堆

         10
       /    \
      7      9
     / \    / \
    5   6  8   3

二叉搜索树

         7
       /   \
      3     9
     / \   / \
    2   5 8   10

平衡二叉搜索树 - AVL 树

当二叉搜索树多次删除或插入元素后可能导致退化成链表，所以在操作后需要旋转节点，使其恢复成平衡的二叉搜索树

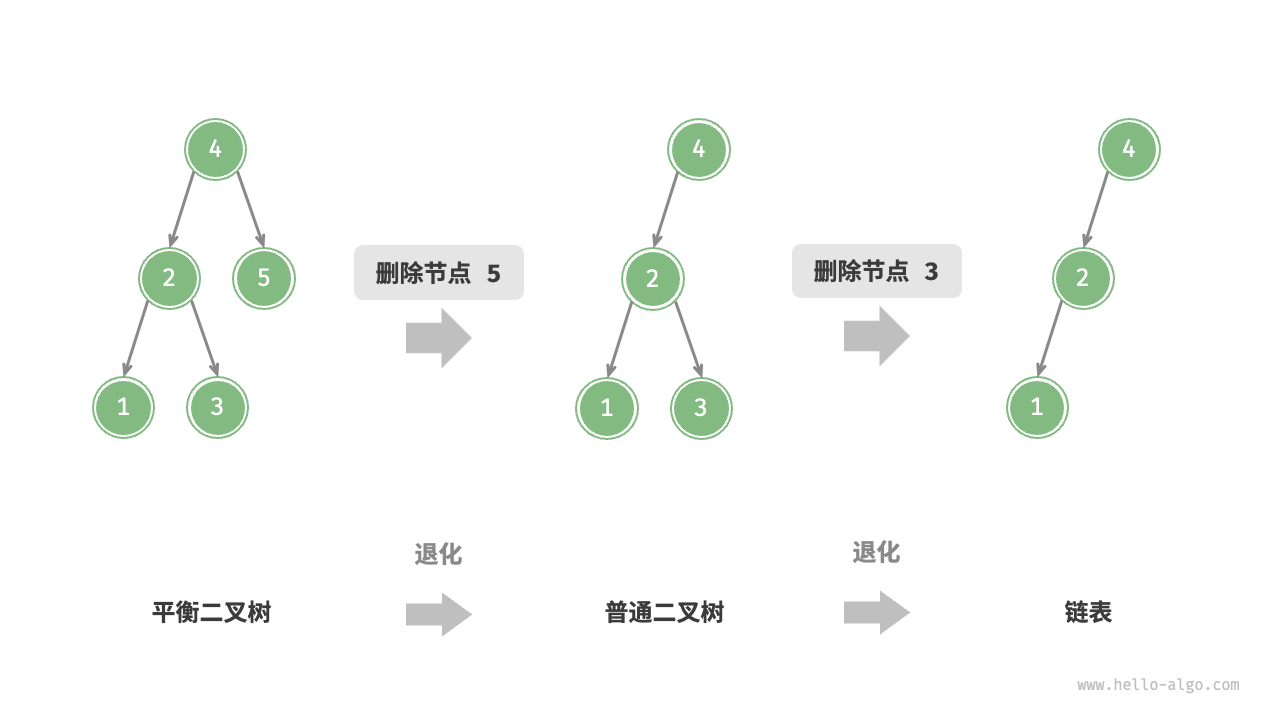
从叶子节点开始一直到根节点，路径上的任意节点左右子树高度差大于1就旋转，可能左旋、右旋、先左后右、先右后左旋

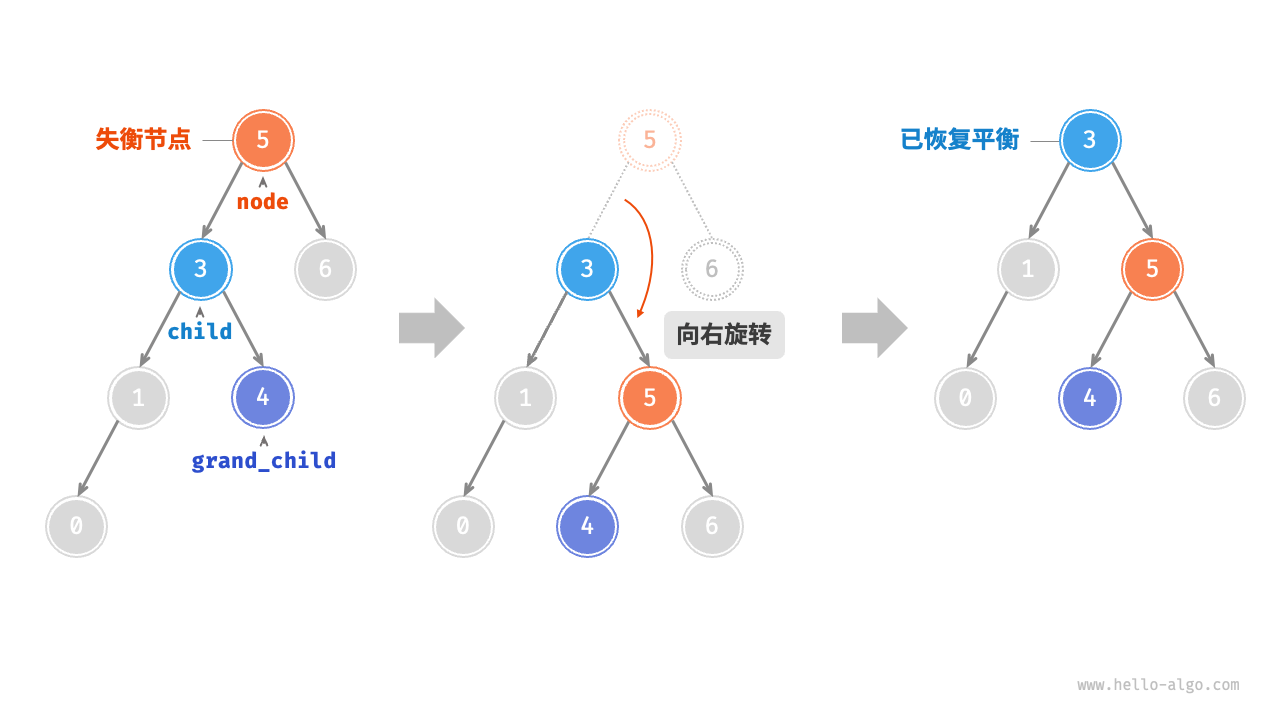
平衡二叉搜索树 - 红黑树

1. 根节点是黑色
2. 节点为红色或黑色
3. NIL 节点（空叶子节点）为黑色
4. 红色节点的子节点为黑色（红色列电不能相邻）
5. 从根节点到 NIL 节点的每条路径上的黑色节点数量相同

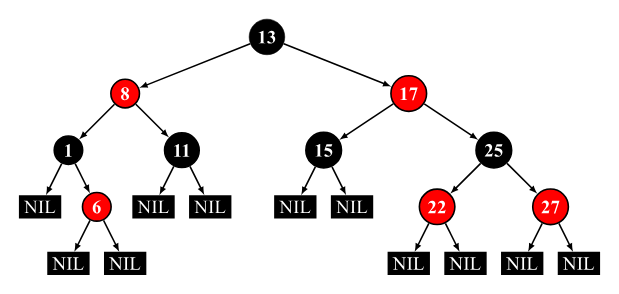
PS：AVL 树 VS 红黑树

特性	AVL 树	红黑树
平衡标准	严格（高度差≤1）	宽松（最长路径≤2倍最短路径）
旋转频率	高	低
插入旋转概率	~50%	~30%
删除旋转概率	几乎总是	有时需要
修复手段	主要靠旋转	旋转+颜色翻转
使用场景	查询特别多，远大于新增、删除	查询和删除、新增都比较多

平衡标准：

• AVL 树：严格要求任何节点的左右子树高度差不超过1（严格平衡）
• 红黑树：通过颜色规则保证从根到叶子的最长路径不超过最短路径的2倍（宽松平衡）

修复策略：

• AVL 树：
  • 从插入点向上回溯到根节点，沿途逐层调整平衡
  • 删除更复杂更叶子节点向上回溯
• 红黑树：
  • 插入最多需要2次旋转（在LR或RL情况下）
  • 删除最多需要3次旋转
  • 修复过程通常只需要局部调整，不需要回溯到根节点
  • 独特的修复手段 颜色翻转，可以在不旋转的情况下通过改变节点颜色来恢复平衡。这种操作比旋转代价小很多