矩阵相关 matrix 1351, 6,73, 3446

1351. Count Negative Numbers in a Sorted Matrix

Easy

338393Add to ListShare

Given a m x n matrix grid which is sorted in non-increasing order both row-wise and column-wise, return the number of negative numbers in grid.

 Example 1:

Input: grid = [[4,3,2,-1],[3,2,1,-1],[1,1,-1,-2],[-1,-1,-2,-3]]
Output: 8
Explanation: There are 8 negatives number in the matrix.

Example 2:

Input: grid = [[3,2],[1,0]]
Output: 0

 Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• -100 <= grid[i][j] <= 100

解法1: O(MN)

class Solution:
    def countNegatives(self, grid: List[List[int]]) -> int:
        count = 0
        def dfs(x, y):  
            if x < 0 or y < 0 or grid[x][y] >= 0:
                return
            nonlocal count
            count += 1
            grid[x][y] = 1
            dfs(x - 1, y)
            dfs(x, y - 1)
        m, n = len(grid), len(grid[0])
        dfs(m - 1, n - 1)
        return count

解法2:O(MlogN)

class Solution:
    def countNegatives(self, grid: List[List[int]]) -> int:
        def bs(row: List[int]):
            left, right = 0, len(row) - 1
            result = -1
            while left <= right:
                mid = left + (right - left) // 2
                if row[mid] >= 0:
                    left = mid + 1
                else:
                    result = mid
                    right = mid - 1
            return result
        total = 0
        for row in grid:
            pos = bs(row)
            if pos >= 0:
                total += len(row) - pos
        return total

解法3: O(M+N)

class Solution:
    def countNegatives(self, grid: List[List[int]]) -> int:
        m = len(grid[0])
        #定义最后一个不小于0的位置
        currPos = m - 1
        result = 0
        for row in grid:
            #如果小于0，那么向左移动。 
            #思考为什么要这样？因为整个矩阵是从左到右，从上到下递减的
            while currPos >= 0 and row[currPos] < 0:
                currPos -= 1
            result += m - currPos - 1
        return result

 

6. Zigzag Conversion

The string "PAYPALISHIRING" is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)

P   A   H   N
A P L S I I G
Y   I   R

And then read line by line: "PAHNAPLSIIGYIR"

Write the code that will take a string and make this conversion given a number of rows:

string convert(string s, int numRows);

Example 1:

Input: s = "PAYPALISHIRING", numRows = 3
Output: "PAHNAPLSIIGYIR"

Example 2:

Input: s = "PAYPALISHIRING", numRows = 4
Output: "PINALSIGYAHRPI"
Explanation:
P     I    N
A   L S  I G
Y A   H R
P     I

Example 3:

Input: s = "A", numRows = 1
Output: "A"

Constraints:

• 1 <= s.length <= 1000
• s consists of English letters (lower-case and upper-case), ',' and '.'.
• 1 <= numRows <= 1000

关键点：

1.实际不需要考虑左右位置问题，关键归属哪行，最后是要合并到一起输出，并没有zigzag空格

2.找到规律，每次都是从row=0开始向下走，到了row=numRows-1又开始向上走

class Solution:
    def convert(self, s: str, numRows: int) -> str:
        #如果只有一行，那么直接输出
        if numRows == 1:
          return s
        #否则申请一个numRows大小的二维list
        arr = [[] for i in range(numRows)]
        step = 1
        row = 0
        for c in s:
          arr[row].append(c)
          row += step
          #如果到了最后一行那么向上返
          if row == numRows - 1:
            step = -1
          #如果到了第一行，那么向下走
          elif row == 0:
            step = 1
        #最后将二维str join起来
        return ''.join([ele for sublist in arr for ele in sublist])

 

73. Set Matrix Zeroes

Medium

12587640Add to ListShare

Given an m x n integer matrix matrix, if an element is 0, set its entire row and column to 0's.

You must do it in place.

Example 1:

Input: matrix = [[1,1,1],[1,0,1],[1,1,1]]
Output: [[1,0,1],[0,0,0],[1,0,1]]

Example 2:

Input: matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
Output: [[0,0,0,0],[0,4,5,0],[0,3,1,0]]

 

Constraints:

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -231 <= matrix[i][j] <= 231 - 1 

Follow up:

• A straightforward solution using O(mn) space is probably a bad idea.
• A simple improvement uses O(m + n) space, but still not the best solution.
• Could you devise a constant space solution?

 

1.使用第一行/第一列来标识某行/某列是否存在0

2.问题是这样会导致我们无法判定第一行/第一列是否存在0，使用row0和col0来标识

class Solution {
    public void setZeroes(int[][] matrix) {
        if(matrix==null || matrix.length==0 || matrix[0].length==0) return;
        boolean row0=false,col0=false;
        for(int i=0;i<matrix.length;i++){
            for(int j=0;j<matrix[0].length;j++){
                if(matrix[i][j]==0){
                    if(i==0) row0=true;
                    if(j==0) col0=true;
                    matrix[0][j]=0;
                    matrix[i][0]=0;
                }
            }
        }
        for(int i=1;i<matrix.length;i++){
            for(int j=1;j<matrix[0].length;j++){
                if(matrix[i][0]==0 || matrix[0][j]==0)
                    matrix[i][j]=0;
            }
        }
        if(col0)
            for(int i=0;i<matrix.length;i++) matrix[i][0]=0;
        if(row0)
            for(int i=0;i<matrix[0].length;i++) matrix[0][i]=0;
        
    }
}

 

3446. Sort Matrix by Diagonals

You are given an n x n square matrix of integers grid. Return the matrix such that:

• The diagonals in the bottom-left triangle (including the middle diagonal) are sorted in non-increasing order.
• The diagonals in the top-right triangle are sorted in non-decreasing order. 

Example 1:

Input: grid = [[1,7,3],[9,8,2],[4,5,6]]

Output: [[8,2,3],[9,6,7],[4,5,1]]

Explanation:

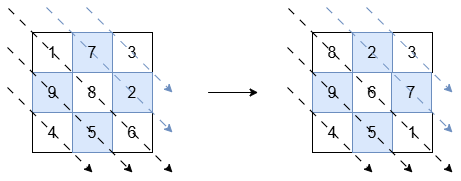
The diagonals with a black arrow (bottom-left triangle) should be sorted in non-increasing order:

• [1, 8, 6] becomes [8, 6, 1].
• [9, 5] and [4] remain unchanged.

The diagonals with a blue arrow (top-right triangle) should be sorted in non-decreasing order:

• [7, 2] becomes [2, 7].
• [3] remains unchanged.

Example 2:

Input: grid = [[0,1],[1,2]]

Output: [[2,1],[1,0]]

Explanation:

The diagonals with a black arrow must be non-increasing, so [0, 2] is changed to [2, 0]. The other diagonals are already in the correct order.

Example 3:

Input: grid = [[1]]

Output: [[1]]

Explanation:

Diagonals with exactly one element are already in order, so no changes are needed.

Constraints:

• grid.length == grid[i].length == n
• 1 <= n <= 10
• -105 <= grid[i][j] <= 105

class Solution {
    public int[][] sortMatrix(int[][] grid) {
        int m = grid.length;
        Map<Integer, List<Integer>> g = new HashMap<>();
        // 按diagonal收集元素
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < m; j++) {
                g.computeIfAbsent(i - j, k -> new ArrayList<>()).add(grid[i][j]);
            }
        }
　　　　 // 排序
        for(int i = -m + 1; i < m; i++) {
            if(i >= 0) Collections.sort(g.get(i), (x, y) -> y - x);
            else Collections.sort(g.get(i), (x, y) -> x - y);
        }
        // 元素回填
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < m; j++) {
                grid[i][j] = g.get(i - j).get((i + j - Math.abs(i - j)) / 2) ;
            }
        }
        return grid;
    }
    record Pos(int x, int y){ }
}

空间优化：

class Solution {
    public int[][] sortMatrix(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int k = m + n - 1;

        for(int i = 1; i <= k; i++) {
            // 计算起始点位置
            int xs = Math.max(i - m, 0), ys = Math.max(n - i, 0);
            List<Integer> list = new ArrayList<>();

            // 收集元素
            int x = xs, y = ys;
            while(x >= 0 && x < m && y >= 0 && y < n) {
                list.add(grid[x++][y++]);
            }

            // 排序
            if(i >= m) Collections.sort(list, (a, b) -> b - a);
            else Collections.sort(list);

            // 回填
            x = xs; 
            y = ys;
            int ind = 0;
            while(x < m && x >= 0 && y >= 0 && y < m) {
                grid[x++][y++] = list.get(ind++);
            }
        }
        return grid;
    }
}