背包问题
01背包
假设有4个背包(weight,contribute),(2,1),(3,3),(4,5),(7,9)
总重量:totalWeight = 10, 在不超过totalWeight的情况下如何使得contribute最大?每个背包最多只能使用一次
下面 i 表示前 i 个背包可选,j 表示totalWeight
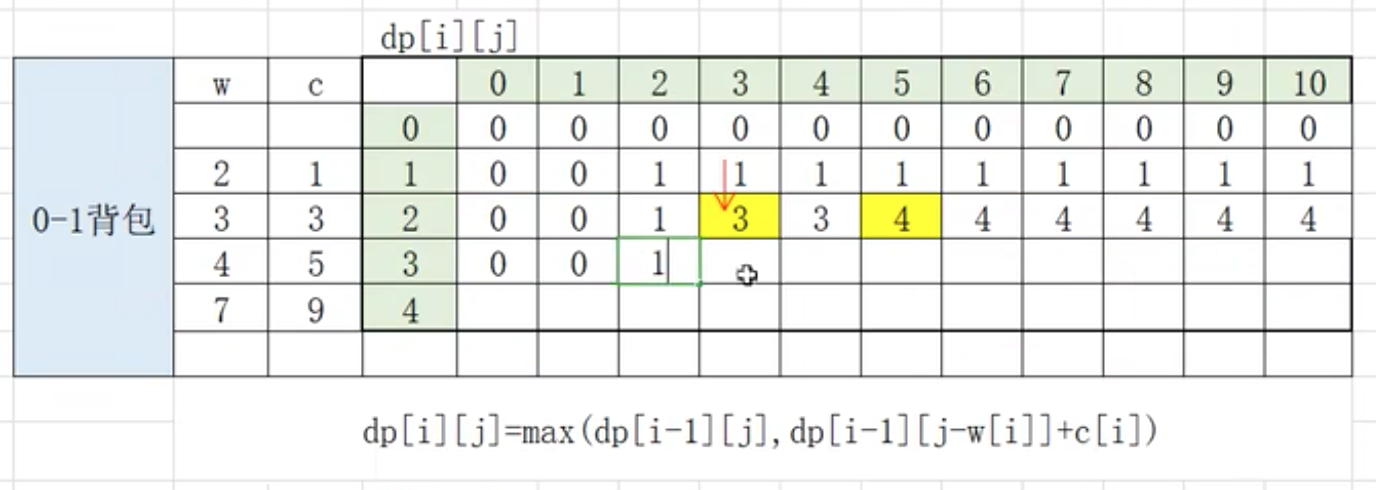
前i个背包可选&最大容量为j的情况下(dp[i][j]) : 可以实现的最大价值为 不选第i个背包(dp[i-1][j]) 和 选第i个背包(dp[i-1][j-w[i]]+c[i]) 的最大值.
package pack; import java.util.Arrays; public class KnapSack {
public static int getMax01(int[] b, int[] w, int total){ // b 是benifit, w 是weight或者cost int[][] mem = new int[b.length+1][total+1]; for(int i=1;i<=b.length;i++){//轮巡所有的背包 for(int j=1;j<=total;j++){//轮巡weight:0~totalWeight mem[i][j] = mem[i-1][j];
//如果当前背包(w[i-1])小于等于背包总容量,那么可以尝试用上当前背包(b[i-1]),再加上剩余的j-w[i-1]能放的最大价值 if(w[i-1]<=j) mem[i][j] = Math.max(mem[i][j], mem[i-1][j-w[i-1]]+b[i-1]); } } return mem[b.length][total]; }
//第二种是在上面基础上进行的优化:将dp mem从二维降到一维 public static int getMax01Optimize(int[] b, int[] w, int total){ int[] mem = new int[total+1]; for(int i=1;i<=b.length;i++){
//从右向左扫描,为啥?因为我们要用到上一行的结果,因此上一行的结果不能覆盖,这块还是不太能解释的清楚??? for(int j=total;j>=1;j--){ mem[j] = mem[j]; if(w[i-1]<=j) mem[j] = Math.max(mem[j], mem[j-w[i-1]]+b[i-1]); } System.out.println(Arrays.toString(mem)); } return mem[total]; }public static void main(String[] args) { // System.out.println(getMax(new int[]{1,2,4,2,5},new int[]{1,2,3,2,5},10)); System.out.println(getMax01Optimize(new int[]{1,2,4,2,5},new int[]{1,2,3,2,5},10)); System.out.println(getMaxAllPackOptimize(new int[]{1,2,4,2,5},new int[]{1,2,3,2,5},10)); } }
类似的题目, coin change
给一列定制化的硬币,如何凑出最接近指定amount的钱但是不能超过amount,例如:
coinlist=[1,2,5], amount = 5. 那么可以凑出 amount的钱
coinlist=[2,4,4,6], amount = 9, 那么可以凑出最接近的是:8
跟上面唯一不同的是,背包存在重量和价值不对等的情况,但是硬币不存在。 那么weight 和 cost都是coins
public class Test { public static void main(String[] args) { System.out.println(change(8, new int[]{2,4,4,8})); } public static int change(int amount, int[] coins) { int[][] dp = new int[coins.length + 1][amount + 1]; for(int i = 1; i <= coins.length; i++) { for(int j = 0; j <= amount; j++) {
// 先继承没有当前硬币情况下(i-1)的结果 dp[i][j] = dp[i - 1][j];
// 如果当前要凑的amount大于等于当前硬币面额, 那么可以尝试加入当前硬币(coins[i - 1]) if(j >= coins[i - 1]) { dp[i][j] = Math.max(dp[i - 1][j - coins[i - 1]] + coins[i - 1], dp[i][j]); } } } return dp[coins.length][amount]; } }
Minimum sum partition
Given an array arr of size n containing non-negative integers, the task is to divide it into two sets S1 and S2 such that the absolute difference between their sums is minimum and find the minimum difference
Example 1:
Input: N = 4, arr[] = {1, 6, 11, 5}
Output: 1
Explanation:
Subset1 = {1, 5, 6}, sum of Subset1 = 12
Subset2 = {11}, sum of Subset2 = 11
Input: N = 2, arr[] = {1, 4}
Output: 3
Explanation:
Subset1 = {1}, sum of Subset1 = 1
Subset2 = {4}, sum of Subset2 = 4
Your Task:
You don't need to read input or print anything. Complete the function minDifference() which takes N and array arr as input parameters and returns the integer value
Expected Time Complexity: O(N*|sum of array elements|)
Expected Auxiliary Space: O(N*|sum of array elements|)
Constraints:
1 ≤ N*|sum of array elements| ≤ 106
0 < arr[i] <= 105
class Solution { public int minDifference(int arr[], int n) { // get total, target = total/2; int total = 0; for (int e : arr) total += e; // int result = change(total / 2, arr); return total - result * 2; }
// coin change 模版,一行没改 public int change(int amount, int[] coins) { int[][] dp = new int[coins.length + 1][amount + 1]; for(int i = 1; i <= coins.length; i++) { for(int j = 0; j <= amount; j++) { dp[i][j] = dp[i - 1][j]; if(j >= coins[i - 1]) { dp[i][j] = Math.max(dp[i - 1][j - coins[i - 1]] + coins[i - 1], dp[i][j]); } } } return dp[coins.length][amount]; } }
416. Partition Equal Subset Sum
Given a non-empty array nums containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.
Example 1:
Input: nums = [1,5,11,5] Output: true Explanation: The array can be partitioned as [1, 5, 5] and [11].
Example 2:
Input: nums = [1,2,3,5] Output: false Explanation: The array cannot be partitioned into equal sum subsets.
Constraints:
1 <= nums.length <= 2001 <= nums[i] <= 100
解法: 又是一道套娃题, 跟上面一题类似
class Solution { public boolean canPartition(int[] nums) { int total = 0; for (int num : nums) total += num; if(total % 2 != 0) return false; int result = change(total / 2, nums); return result == total / 2; } // coin change 模版,一行没改 public int change(int amount, int[] coins) { int[][] dp = new int[coins.length + 1][amount + 1]; for(int i = 1; i <= coins.length; i++) { for(int j = 0; j <= amount; j++) { dp[i][j] = dp[i - 1][j]; if(j >= coins[i - 1]) { dp[i][j] = Math.max(dp[i - 1][j - coins[i - 1]] + coins[i - 1], dp[i][j]); } } } return dp[coins.length][amount]; } }
完全背包
假设有4个背包(weight,contribute),(2,1),(3,3),(4,5),(7,9)
总重量:totalWeight = 10, 在不超过totalWeight的情况下如何使得contribute最大?每个背包可以无限次使用
下面 i 表示前 i 个背包可选,j 表示totalWeight
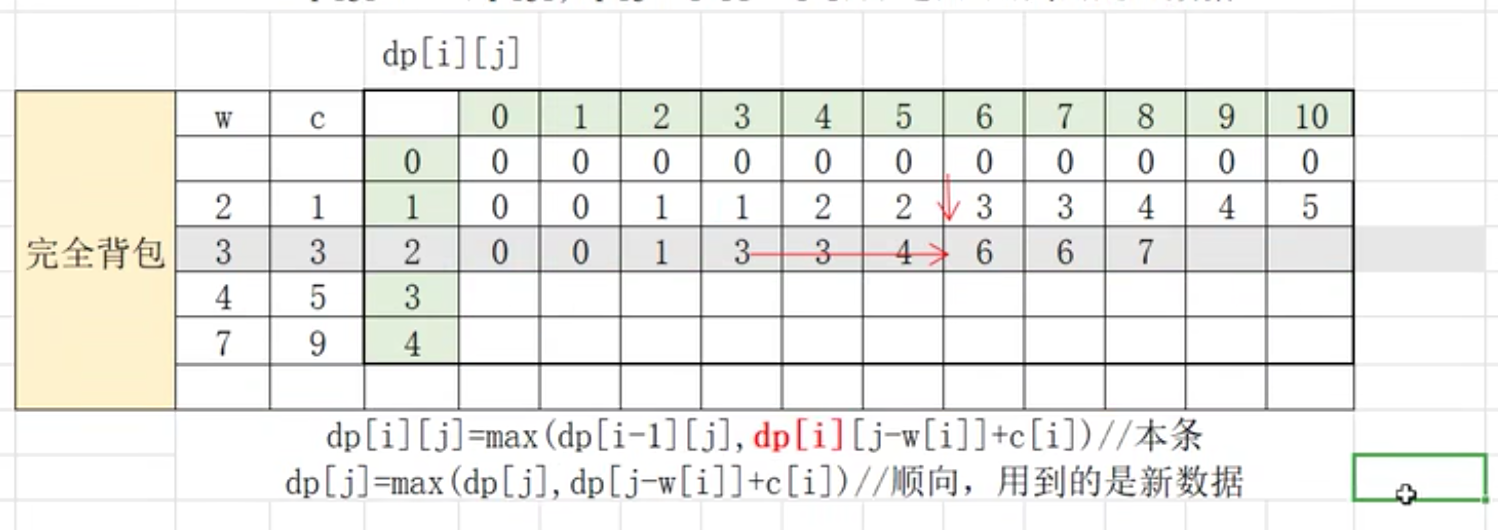
前i个背包可选&最大容量为j的情况下(dp[i][j]) 最大价值为: 前i-1个背包可选情况下的最大值 和 前i个背包(dp[i-1][j-w[i]]+c[i]) 的最大值.
package pack; import java.util.Arrays; public class KnapSack { public static int getMaxAllPack(int[] b, int[] w, int total){ int[][] mem = new int[b.length+1][total+1]; for(int i=1;i<=b.length;i++){ for(int j=1;j<=total;j++){ mem[i][j] = mem[i-1][j];
//对比01背包,唯一不同的是:01背包取的是mem[i - 1]..., 这里是mem[i], 原因是此处硬币可以重复使用
if(w[i-1]<=j) mem[i][j] = Math.max(mem[i][j], mem[i][j-w[i-1]]+b[i-1]); } } return mem[b.length][total]; } public static int getMaxAllPackOptimize(int[] b, int[] w, int total){ int[] mem = new int[total+1]; for(int i=1;i<=b.length;i++){ for(int j=1;j<=total;j++){ if(w[i-1]<=j) mem[j] = Math.max(mem[j], mem[j-w[i-1]]+b[i-1]); } } return mem[total]; } public static void main(String[] args) { System.out.println(getMaxAllPackOptimize(new int[]{1,2,4,2,5},new int[]{1,2,3,2,5},10)); } }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号