dfs 785,803,

785. Is Graph Bipartite?

Medium

4979279Add to ListShare

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

• There are no self-edges (graph[u] does not contain u).
• There are no parallel edges (graph[u] does not contain duplicate values).
• If v is in graph[u], then u is in graph[v] (the graph is undirected).
• The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

 

Example 1:

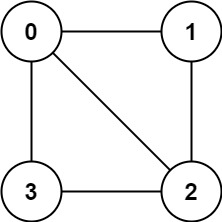
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

 

Constraints:

• graph.length == n
• 1 <= n <= 100
• 0 <= graph[u].length < n
• 0 <= graph[u][i] <= n - 1
• graph[u] does not contain u.
• All the values of graph[u] are unique.
• If graph[u] contains v, then graph[v] contains u.

class Solution {
    public boolean isBipartite(int[][] graph) {
        int[] color = new int[graph.length];
        Arrays.fill(color,-1);
        for(int i=0;i<graph.length;i++){//坑点，有可能这个图压根就不连通，因此需要把所有点都过一遍
            if(color[i]==-1){
                if(!dfs(graph, i, color, 0)) return false;
            }
        }
        return true;
    }
    private boolean dfs(int[][] graph, int node, int[] color, int nextColor){
        if(color[node]!=-1 ) return color[node]==nextColor;
        color[node] = nextColor;
        for(int other:graph[node]){
            if(!dfs(graph, other, color, 1-nextColor)) return false;
        }
        return true;
    }
}

 

802. Find Eventual Safe States

Medium

2286325Add to ListShare

There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].

A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node.

Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.

 

Example 1:

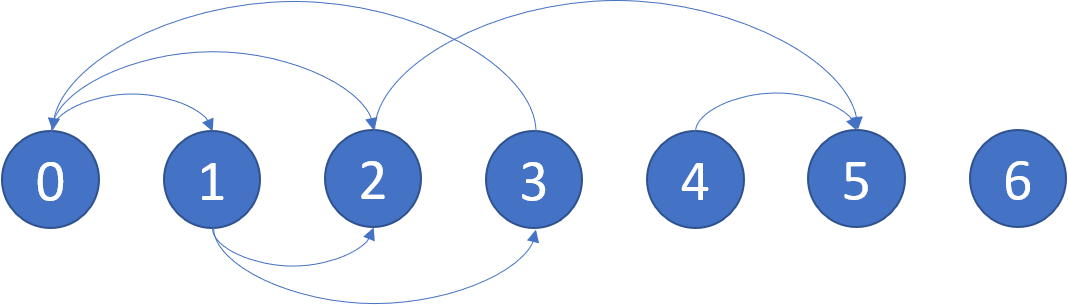
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Explanation: The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.

Example 2:

Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
Output: [4]
Explanation:
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.

 Constraints:

• n == graph.length
• 1 <= n <= 104
• 0 <= graph[i].length <= n
• 0 <= graph[i][j] <= n - 1
• graph[i] is sorted in a strictly increasing order.
• The graph may contain self-loops.
• The number of edges in the graph will be in the range [1, 4 * 104].

class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        int[] flag = new int[graph.length];
        List<Integer> list = new ArrayList();
        for(int i=0;i<graph.length;i++){
            if(dfs(graph, i, flag) == 2) list.add(i);
        }
        return list;
    }
    //flag[]  0:init 1:travesing 2:complete 3:cycle
    private int dfs(int[][] graph, int curr, int[] flag){
        if(flag[curr] != 0) return flag[curr];
        flag[curr] = 1;
        boolean currFlag = false;
        for(int other:graph[curr]){
            int result = dfs(graph, other, flag);
            if( result == 1 || result ==3){
                currFlag = true;
            }
        }
        if(currFlag) flag[curr] = 3;
        else flag[curr] = 2;
        return flag[curr];
    }
}