图基础算法（四）- 拓扑排序 toplogical sort 269,2115,1361

269. Alien Dictionary

There is a new alien language that uses the English alphabet. However, the order among the letters is unknown to you.

You are given a list of strings words from the alien language's dictionary, where the strings in words are sorted lexicographically by the rules of this new language.

Return a string of the unique letters in the new alien language sorted in lexicographically increasing order by the new language's rules. If there is no solution, return "". If there are multiple solutions, return any of them.

A string s is lexicographically smaller than a string t if at the first letter where they differ, the letter in s comes before the letter in t in the alien language. If the first min(s.length, t.length) letters are the same, then s is smaller if and only if s.length < t.length.

Example 1:

Input: words = ["wrt","wrf","er","ett","rftt"]
Output: "wertf"

Example 2:

Input: words = ["z","x"]
Output: "zx"

Example 3:

Input: words = ["z","x","z"]
Output: ""
Explanation: The order is invalid, so return "".

Constraints:

• 1 <= words.length <= 100
• 1 <= words[i].length <= 100
• words[i] consists of only lowercase English letters.

坑点：

1.一定要把所有的字母都放入indegree，否则输出的时候只会输出有dependency的

2.会有一种非法case是：["abc","ab"]

 

class Solution {
    public String alienOrder(String[] words) {
        //graph
        Map<Character, List<Character>> graph = new HashMap<>();
        //indegree
        Map<Character, Integer> indegree= new HashMap<>();
        //所有元素放入degree，这样便利的时候不会漏  坑点1
        for(String word : words) {
            for(char c : word.toCharArray()) {
                indegree.put(c, 0);
            }
        }
        //words中的单词，两两比对，找到他们的差异点，即为某两个字母前后顺序
        for(int i = 1; i < words.length; i++) {
            String first = words[i - 1], second = words[i];
            //特殊非法场景 [abc, ab]  坑点2
            if(first.length() > second.length() && first.startsWith(second)) return "";
            for(int j = 0; j < Math.min(first.length(), second.length()); j++) {
                char c1 = first.charAt(j), c2 = second.charAt(j);
                if(c1 == c2) continue;
                //建立依赖关系
                graph.computeIfAbsent(c1, k -> new ArrayList()).add(c2);
                //添加degree
                indegree.put(c2, indegree.get(c2) + 1);
                break;
            }
        }
        //拓扑遍历
        Queue<Character> queue = new LinkedList<>();
        //0 degree的先入队列
        for(char c : indegree.keySet()) {
            if(indegree.get(c) == 0) {
                queue.offer((char)(c));
            }
        }
        StringBuffer sb = new StringBuffer();
        //bfs 遍历
        while(!queue.isEmpty()) {
            char curr = queue.poll();
            sb.append(curr);
            for(char other : graph.getOrDefault(curr, List.of())) {
                indegree.put(other, indegree.get(other) - 1);
                if(indegree.get(other) == 0) queue.offer(other);
            }
        }
        if(sb.length() < indegree.size()) return "";
        return sb.toString();
    }
}
/**

"wrt","wrf","er","ett","rftt"
t->f
w->e
r->t
e->r


t:1
f:1
w:0


 */

 

 

 

 

 2115. Find All Possible Recipes from Given Supplies

Medium

You have information about n different recipes. You are given a string array recipes and a 2D string array ingredients. The ith recipe has the name recipes[i], and you can create it if you have all the needed ingredients from ingredients[i]. Ingredients to a recipe may need to be created from other recipes, i.e., ingredients[i] may contain a string that is in recipes.

You are also given a string array supplies containing all the ingredients that you initially have, and you have an infinite supply of all of them.

Return a list of all the recipes that you can create. You may return the answer in any order.

Note that two recipes may contain each other in their ingredients.

 Example 1:

Input: recipes = ["bread"], ingredients = [["yeast","flour"]], supplies = ["yeast","flour","corn"]
Output: ["bread"]
Explanation:
We can create "bread" since we have the ingredients "yeast" and "flour".

Example 2:

Input: recipes = ["bread","sandwich"], ingredients = [["yeast","flour"],["bread","meat"]], supplies = ["yeast","flour","meat"]
Output: ["bread","sandwich"]
Explanation:
We can create "bread" since we have the ingredients "yeast" and "flour".
We can create "sandwich" since we have the ingredient "meat" and can create the ingredient "bread".

Example 3:

Input: recipes = ["bread","sandwich","burger"], ingredients = [["yeast","flour"],["bread","meat"],["sandwich","meat","bread"]], supplies = ["yeast","flour","meat"]
Output: ["bread","sandwich","burger"]
Explanation:
We can create "bread" since we have the ingredients "yeast" and "flour".
We can create "sandwich" since we have the ingredient "meat" and can create the ingredient "bread".
We can create "burger" since we have the ingredient "meat" and can create the ingredients "bread" and "sandwich".

 Constraints:

• n == recipes.length == ingredients.length
• 1 <= n <= 100
• 1 <= ingredients[i].length, supplies.length <= 100
• 1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10
• recipes[i], ingredients[i][j], and supplies[k] consist only of lowercase English letters.
• All the values of recipes and supplies combined are unique.
• Each ingredients[i] does not contain any duplicate values.

class Solution {
    public List<String> findAllRecipes(String[] recipes, List<List<String>> ingredients, String[] supplies) {
        //build graph
        Map<String,List<String>> map = new HashMap();
        Map<String,Integer> degree = new HashMap();
        for(int i=0;i<recipes.length;i++){
            String recipe = recipes[i];
            for(String ingre:ingredients.get(i)){
                List<String> list = map.getOrDefault(ingre,new ArrayList());
                list.add(recipe);
                map.put(ingre,list);
            }
            degree.put(recipe,ingredients.get(i).size());
        }
        Set<String> set = new HashSet(Arrays.asList(recipes));
        //bfs 
        Queue<String> queue = new LinkedList();
        for(String temp:supplies) queue.offer(temp);
        
        List<String> result = new ArrayList();
        while(!queue.isEmpty()){
            String curr = queue.poll();
            if(set.contains(curr)) result.add(curr);//如果当前元素在recipe列表中，那么我们将其加入结果集
            for(String next:map.getOrDefault(curr,Arrays.asList())){
                if(degree.getOrDefault(next,1)==1){
                    queue.offer(next);
                }
                degree.put(next,degree.getOrDefault(next,1)-1);
            }
        }
        return result;
    }
}

 1361. Validate Binary Tree Nodes

Medium

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

 Example 1:

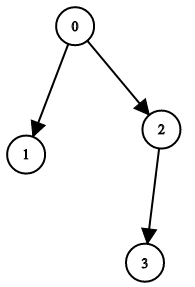
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

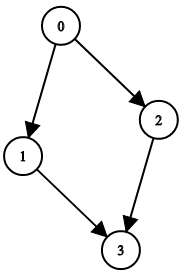
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

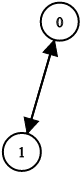
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

Constraints:

• n == leftChild.length == rightChild.length
• 1 <= n <= 104
• -1 <= leftChild[i], rightChild[i] <= n - 1

class Solution {
    /*
    满足这个二叉树所需的充分条件，从toplogical的角度来看：
    1.root只有1个，即indegree为0的点只有1个
    2.因为是树状，因此toplogical traversal的时候不会有重复访问
    3.不存在不联通的点，因此可以一次toplogical traversal所有的点
    */
    public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
        int[] indegree = new int[n];
        for(int i=0;i<n;i++){
            if(leftChild[i] != -1) indegree[leftChild[i]]++;
            if(rightChild[i] != -1) indegree[rightChild[i]]++;
        }
        List<Integer> roots = new ArrayList();
        for(int i=0;i<n;i++){
            if(indegree[i] == 0) roots.add(i);
        }
        //入度为0的点，只应该有一个
        if(roots.size() != 1) return false;
        int root = roots.get(0);
        //从root开始进行拓扑遍历
        Queue<Integer> queue = new LinkedList();
        boolean[] visited = new boolean[n];
        visited[root] = true;
        queue.offer(root);
        while(!queue.isEmpty()){
            int curr = queue.poll();
            if(leftChild[curr]!=-1){
                //如果存在已经被访问过的点，那么说明路径有交叉，就不满足树的条件
                if(visited[leftChild[curr]]) return false;
                visited[leftChild[curr]] = true;
                queue.offer(leftChild[curr]);
            }
            if(rightChild[curr]!=-1){
                //如果存在已经被访问过的点，那么说明路径有交叉，就不满足树的条件
                if(visited[rightChild[curr]]) return false;
                visited[rightChild[curr]] = true;
                queue.offer(rightChild[curr]);
            }
        }
        //判断是否所有的点都被访问过了，如果没有，所有节点没有完全联通，不是合法的树
        for(int i=0;i<n;i++){
            if(!visited[i]) return false;
        }
        return true;
    }
}

 802. Find Eventual Safe States

Medium

2922340Add to ListShare

There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].

A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node (or another safe node).

Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.

 

Example 1:

Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Explanation: The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.

Example 2:

Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
Output: [4]
Explanation:
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.

 Constraints:

• n == graph.length
• 1 <= n <= 104
• 0 <= graph[i].length <= n
• 0 <= graph[i][j] <= n - 1
• graph[i] is sorted in a strictly increasing order.
• The graph may contain self-loops.
• The number of edges in the graph will be in the range [1, 4 * 104].

class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        int m = graph.length;
        List<Integer>[] rg = new List[m];
        int[] outdegree = new int[m];
        for(int i = 0; i < m; i++) rg[i] = new ArrayList();
        for(int i = 0; i < m; i++){
            for(int other : graph[i]){
                outdegree[i]++;
                rg[other].add(i);
            }
        }
        List<Integer> list = new ArrayList();
        Queue<Integer> queue = new LinkedList();
        for(int i = 0; i < m; i++){
            if(outdegree[i] == 0) queue.offer(i);
        }
        while(!queue.isEmpty()){
            int curr = queue.poll();
            list.add(curr);
            for(int other : rg[curr]){
                outdegree[other]--;
                if(outdegree[other] == 0) queue.offer(other);
            }
        }
        Collections.sort(list);
        return list;
    }
}

310. Minimum Height Trees

Medium

6126263Add to ListShare

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h))  are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

 

Example 1:

Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

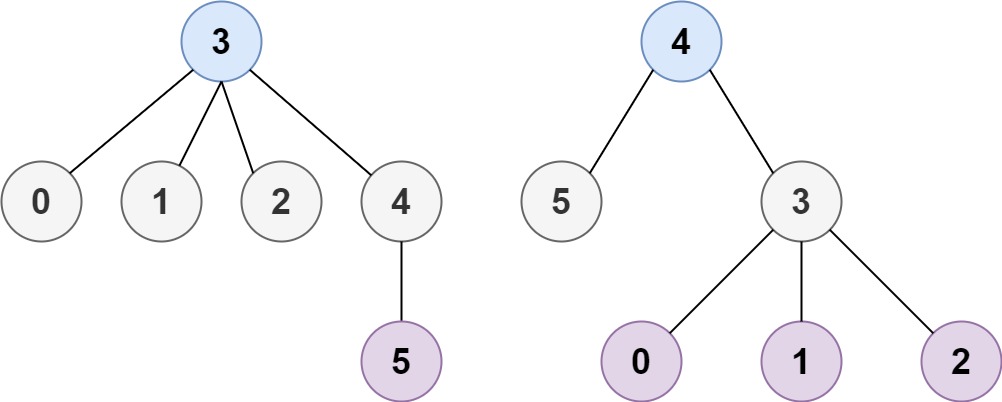
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Constraints:

• 1 <= n <= 2 * 104
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• All the pairs (ai, bi) are distinct.
• The given input is guaranteed to be a tree and there will be no repeated edges.

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        if(n==1) return Arrays.asList(0);
        Map<Integer,List<Integer>> map = new HashMap();
        int[] degree = new int[n];
        for(int[] edge:edges){
            degree[edge[0]]++;
            degree[edge[1]]++;
            List<Integer> list = map.getOrDefault(edge[0],new ArrayList());
            list.add(edge[1]);
            map.put(edge[0],list);
            List<Integer> list1 = map.getOrDefault(edge[1],new ArrayList());
            list1.add(edge[0]);
            map.put(edge[1],list1);
        }
        Queue<Integer> queue = new LinkedList();
        for(int i=0;i<n;i++){
            if(degree[i]==1){
                queue.offer(i);
            }
        }
        List<Integer> result = new ArrayList();
        while(!queue.isEmpty()){
            int size = queue.size();
            result = new ArrayList(queue);
            for(int i=0;i<size;i++){
                int temp = queue.poll();
                for(int other:map.get(temp)){
                    degree[other]--;
                    if(degree[other]==1){
                        queue.offer(other);
                    }
                }
            }
        }
        return result;
    }
}