最长公共子序列

Longest common subarray in the given two arrays

Given two arrays A[] and B[] of N and M integers respectively, the task is to find the maximum length of equal subarray or the longest common subarray between the two given array.

Examples: 

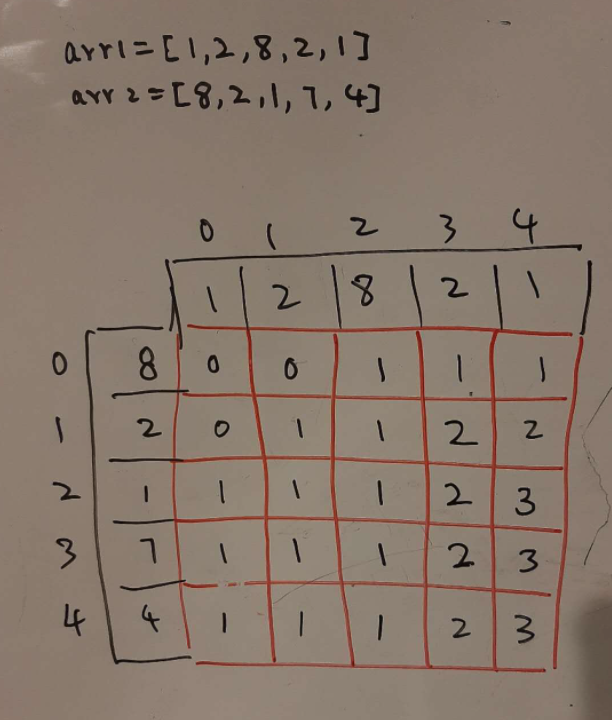
Input: A[] = {1, 2, 8, 2, 1}, B[] = {8, 2, 1, 4, 7} 
Output: 3 
Explanation: 
The subarray that is common to both arrays are {8, 2, 1} and the length of the subarray is 3.
Input: A[] = {1, 2, 3, 2, 1}, B[] = {8, 7, 6, 4, 7} 
Output: 0 
Explanation: 
There is no such subarrays which are equal in the array A[] and B[]. 

 

 

public class LongestCommonSubArray {
    public static void main(String[] args) {
        System.out.println(lcs(new int[]{1,2,8,2,1,5},new int[]{4}));
    }
    private static int lcs(int[] num1,int[] num2){
        int[][] mem = new int[num1.length+1][num2.length+1];
        int max = 0;
        for(int i=1;i<=num1.length;i++){
            for(int j=1;j<=num2.length;j++){
                if(num1[i-1]==num2[j-1]){
                    mem[i][j]=mem[i-1][j-1]+1;
                    max = Math.max(max,mem[i][j]);
                }
            }
        }
        return max;
    }
}

 

1143. Longest Common Subsequence

Medium

536361Add to ListShare

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

• For example, "ace" is a subsequence of "abcde".

A common subsequence of two strings is a subsequence that is common to both strings.

 

Example 1:

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Constraints:

• 1 <= text1.length, text2.length <= 1000
• text1 and text2 consist of only lowercase English characters.

解法一：递归暴力解

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        return recursive(text1,0,text2,0);
    }
    //计算ind1 ind2 到末尾的lcs
    private int recursive(String text1, int ind1, String text2, int ind2){
        if(ind1==text1.length() || ind2==text2.length()) return 0;
        if(text1.charAt(ind1)==text2.charAt(ind2)){//如果当前位置相等，那么直接算各自下一个位置的情况
            return recursive(text1,ind1+1,text2,ind2+1)+1;
        }
        else //如果当前位置不等，那么尝试第一个或者第二个指针右移
            return Math.max(recursive(text1,ind1+1,text2,ind2),recursive(text1,ind1,text2,ind2+1));
    }
}

解法二：上面暴力解有很多的重复计算，在上面暴力解法基础上增加memoization

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        Integer[][] mem = new Integer[text1.length()+1][text2.length()+1];
        return recursive(text1,0,text2,0,mem);
    }
    private int recursive(String text1, int ind1, String text2, int ind2,Integer[][] mem){
        if(mem[ind1][ind2]!=null) return mem[ind1][ind2];
        if(ind1==text1.length() || ind2==text2.length()) return 0;
        
        if(text1.charAt(ind1)==text2.charAt(ind2)){
            mem[ind1][ind2]=recursive(text1,ind1+1,text2,ind2+1,mem)+1;
        }
        else
            mem[ind1][ind2]=Math.max(recursive(text1,ind1+1,text2,ind2,mem),recursive(text1,ind1,text2,ind2+1,mem));
        return mem[ind1][ind2];
    }
}

解法三：dp

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int[][] mem = new int[text1.length()+1][text2.length()+1];
        for(int i=1;i<=text1.length();i++){
            for(int j=1;j<=text2.length();j++){
                if(text1.charAt(i-1)==text2.charAt(j-1)){
                    mem[i][j]=mem[i-1][j-1]+1;
                }
                else{
                    mem[i][j] = Math.max(mem[i][j-1],mem[i-1][j]);
                }
            }
        }
        return mem[text1.length()][text2.length()];
    }
}