前缀和-prefixsum 560,523,525,370, 2536 ,304,528,2488, 2772, 3212, 2251, 3381, 3623, 3714
Given an array of integers nums and an integer k, return the total number of continuous subarrays whose sum equals to k.
Example 1:
Input: nums = [1,1,1], k = 2 Output: 2
Example 2:
Input: nums = [1,2,3], k = 3 Output: 2
Constraints:
1 <= nums.length <= 2 * 104-1000 <= nums[i] <= 1000-107 <= k <= 107
解法：
如果只有正数的情况下，我们可以直接使用sliding window O(N)时间解决
但是这个题是正负数都有，因此需要使用prefix sum解决
| index | 0 | 1 | 2 | 3 |
| arr | 1 | 2 | 3 | -2 |
| prefix sum | 1 | 3 | 6 | 4 |
1.计算prefix sum
2.两层循环配对所有位置计算count
class Solution { public int subarraySum(int[] nums, int k) { int count=0; int[] arr = new int[nums.length+1]; arr[0]=0; for(int i=1;i<arr.length;i++){ arr[i]=arr[i-1]+nums[i-1]; } for(int i=0;i<arr.length-1;i++){ for(int j=i+1;j<arr.length;j++){ if(arr[j]-arr[i]==k) count++; } } return count; } }
时间复杂度 O(N2)
解法2:
prefix sum + hashmap
| index | 0 | 1 | 2 | 3 |
| arr | 1 | 2 | 3 | -2 |
| prefix sum | 1 | 3 | 6 | 4 |
| map | (0:1) (1:1) |
(0:1) (1:1) (3:1) |
(0:1) (1:1) (3:1) (6:1) |
(0:1) (1:1) (3:1) (6:1) (4:1) |
时间复杂度 O(N)
class Solution { public int subarraySum(int[] nums, int k) { int count=0; int[] arr = new int[nums.length+1]; arr[0]=0; for(int i=1;i<arr.length;i++){ arr[i]=arr[i-1]+nums[i-1]; } Map<Integer,Integer> map = new HashMap(); for(int i=0;i<arr.length;i++){ count+=map.getOrDefault(arr[i]-k,0); map.put(arr[i],map.getOrDefault(arr[i],0)+1); } return count; } }
Given an integer array nums and an integer k, return true if nums has a continuous subarray of size at least two whose elements sum up to a multiple of k, or false otherwise.
An integer x is a multiple of k if there exists an integer n such that x = n * k. 0 is always a multiple of k.
Example 1:
Input: nums = [23,2,4,6,7], k = 6
Output: true
Explanation: [2, 4] is a continuous subarray of size 2 whose elements sum up to 6.
Example 2:
Input: nums = [23,2,6,4,7], k = 6
Output: true
Explanation: [23, 2, 6, 4, 7] is an continuous subarray of size 5 whose elements sum up to 42.
42 is a multiple of 6 because 42 = 7 * 6 and 7 is an integer.
Example 3:
Input: nums = [23,2,6,4,7], k = 13 Output: false
Constraints:
1 <= nums.length <= 1050 <= nums[i] <= 1090 <= sum(nums[i]) <= 231 - 11 <= k <= 231 - 1
class Solution { public boolean checkSubarraySum(int[] nums, int k) {
//map中存放 key : prefixsum, value : 该sum的第一次出现的位置 Map<Integer,Integer> map = new HashMap(); map.put(0,-1); int sum=0; for(int i=0;i<nums.length;i++){ sum=(sum+nums[i]%k)%k;//坑点：这个地方很容易越界，另外注意这个题都是正数 //如果这个sum值已经出现过， 1.无需在更新位置，因为它不是第一次出现的位置 2.看本次出现的位置是否于上次出现距离大于1
if(map.get(sum)!=null){ if(i-map.get(sum)>1) return true; } //保存这个sum出现过的位置
else map.put(sum,i); } return false; } }
Given a binary array nums, return the maximum length of a contiguous subarray with an equal number of 0 and 1.
Example 1:
Input: nums = [0,1] Output: 2 Explanation: [0, 1] is the longest contiguous subarray with an equal number of 0 and 1.
Example 2:
Input: nums = [0,1,0] Output: 2 Explanation: [0, 1] (or [1, 0]) is a longest contiguous subarray with equal number of 0 and 1.
Constraints:
1 <= nums.length <= 105nums[i]is either0or1.
class Solution { public int findMaxLength(int[] nums) { //1.将0 翻为 -1 for(int i=0;i<nums.length;i++) if(nums[i]==0) nums[i]=-1; //2.prefixsum ,记录到map求取长度 int max = 0; Map<Integer,Integer> map = new HashMap(); map.put(0,-1); int sum=0; for(int i=0;i<nums.length;i++){ sum+=nums[i]; if(map.get(sum)!=null) max = Math.max(max,i-map.get(sum)); //如果map中已经存在，说明满足条件，记录最大长度 else map.put(sum,i); //如果该sum值还不存在，记录到map } return max; } }
You are given an integer length and an array updates where updates[i] = [startIdxi, endIdxi, inci].
You have an array arr of length length with all zeros, and you have some operation to apply on arr. In the ith operation, you should increment all the elements arr[startIdxi], arr[startIdxi + 1], ..., arr[endIdxi] by inci.
Return arr after applying all the updates.
Example 1:
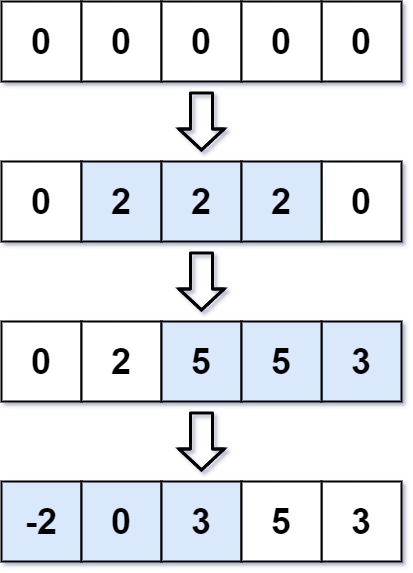
Input: length = 5, updates = [[1,3,2],[2,4,3],[0,2,-2]] Output: [-2,0,3,5,3]
Example 2:
Input: length = 10, updates = [[2,4,6],[5,6,8],[1,9,-4]] Output: [0,-4,2,2,2,4,4,-4,-4,-4]
Constraints:
1 <= length <= 1050 <= updates.length <= 1040 <= startIdxi <= endIdxi < length-1000 <= inci <= 1000
class Solution { public int[] getModifiedArray(int length, int[][] updates) { int[] result = new int[length]; //只在开始位置累加val，在结束位置的下一个位置累减val for(int[] update:updates){ int start = update[0]; int end = update[1]+1; int val = update[2]; result[start]+=val; if(end<length) result[end]-=val; } //最终做一次prefixsum即为最终结果 for(int i=1;i<result.length;i++){ result[i]+=result[i-1]; } return result; } }
You are given a positive integer n, indicating that we initially have an n x n 0-indexed integer matrix mat filled with zeroes.
You are also given a 2D integer array query. For each query[i] = [row1i, col1i, row2i, col2i], you should do the following operation:
- Add
1to every element in the submatrix with the top left corner(row1i, col1i)and the bottom right corner(row2i, col2i). That is, add1tomat[x][y]for for allrow1i <= x <= row2iandcol1i <= y <= col2i.
Return the matrix mat after performing every query.
Example 1:
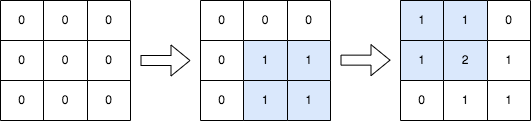
Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]] Output: [[1,1,0],[1,2,1],[0,1,1]] Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query. - In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2). - In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
Example 2:
Input: n = 2, queries = [[0,0,1,1]] Output: [[1,1],[1,1]] Explanation: The diagram above shows the initial matrix and the matrix after the first query. - In the first query we add 1 to every element in the matrix.
Constraints:
1 <= n <= 5001 <= queries.length <= 1040 <= row1i <= row2i < n0 <= col1i <= col2i < n
class Solution { public int[][] rangeAddQueries(int n, int[][] queries) { int[][] result = new int[n][n]; for(int[] query : queries) { int startx = query[0], starty = query[1], endx = query[2], endy = query[3]; //逐行进行 370的标记 for(int i = startx; i <= endx; i++) { result[i][starty] += 1; if(endy + 1 < n) result[i][endy + 1] -= 1; } } //逐行进行prefix sum for(int i = 0; i < n; i++) { for(int j = 1; j < n; j++) { result[i][j] += result[i][j - 1]; } } return result; } }
304. Range Sum Query 2D - Immutable
Given a 2D matrix matrix, handle multiple queries of the following type:
- Calculate the sum of the elements of
matrixinside the rectangle defined by its upper left corner(row1, col1)and lower right corner(row2, col2).
Implement the NumMatrix class:
NumMatrix(int[][] matrix)Initializes the object with the integer matrixmatrix.int sumRegion(int row1, int col1, int row2, int col2)Returns the sum of the elements ofmatrixinside the rectangle defined by its upper left corner(row1, col1)and lower right corner(row2, col2).
Example 1:
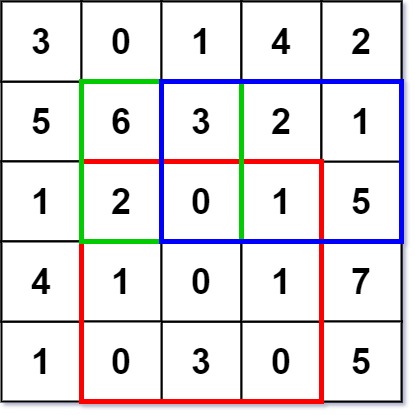
Input ["NumMatrix", "sumRegion", "sumRegion", "sumRegion"] [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]] Output [null, 8, 11, 12] Explanation NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]); numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle) numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle) numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200-105 <= matrix[i][j] <= 1050 <= row1 <= row2 < m0 <= col1 <= col2 < n- At most
104calls will be made tosumRegion.
class NumMatrix { private int[][] result; public NumMatrix(int[][] matrix) { //这个地方使用[matrix.length+1][matrix[0].length+1] ，是因为后面边界条件容易处理 result = new int[matrix.length+1][matrix[0].length+1]; for(int i=0;i<matrix.length;i++){ for(int j=0;j<matrix[0].length;j++){ result[i+1][j+1] = result[i][j+1]+result[i+1][j]-result[i][j]+matrix[i][j]; } } } public int sumRegion(int row1, int col1, int row2, int col2) { return result[row2+1][col2+1] - result[row1][col2+1] - result[row2+1][col1] + result[row1][col1]; } }
528. Random Pick with Weight
You are given a 0-indexed array of positive integers w where w[i] describes the weight of the ith index.
You need to implement the function pickIndex(), which randomly picks an index in the range [0, w.length - 1] (inclusive) and returns it. The probability of picking an index i is w[i] / sum(w).
- For example, if
w = [1, 3], the probability of picking index0is1 / (1 + 3) = 0.25(i.e.,25%), and the probability of picking index1is3 / (1 + 3) = 0.75(i.e.,75%).
Example 1:
Input ["Solution","pickIndex"] [[[1]],[]] Output [null,0] Explanation Solution solution = new Solution([1]); solution.pickIndex(); // return 0. The only option is to return 0 since there is only one element in w.
Example 2:
Input ["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"] [[[1,3]],[],[],[],[],[]] Output [null,1,1,1,1,0] Explanation Solution solution = new Solution([1, 3]); solution.pickIndex(); // return 1. It is returning the second element (index = 1) that has a probability of 3/4. solution.pickIndex(); // return 1 solution.pickIndex(); // return 1 solution.pickIndex(); // return 1 solution.pickIndex(); // return 0. It is returning the first element (index = 0) that has a probability of 1/4. Since this is a randomization problem, multiple answers are allowed. All of the following outputs can be considered correct: [null,1,1,1,1,0] [null,1,1,1,1,1] [null,1,1,1,0,0] [null,1,1,1,0,1] [null,1,0,1,0,0] ...... and so on.
Constraints:
1 <= w.length <= 1041 <= w[i] <= 105pickIndexwill be called at most104times.
class Solution { int[] presum; Random random = new Random(); public Solution(int[] w) { presum = new int[w.length]; for(int i=0;i<w.length;i++){ if(i==0) presum[i]=w[i]; else presum[i]=presum[i-1]+w[i]; } } public int pickIndex() { int ran = random.nextInt(presum[presum.length-1])+1;//这个地方要+1，因为比如：你是1,5,15,16 那么你取[0,16]总是不包含16，如果不+1 永远取不到16 int index = Arrays.binarySearch(presum,ran); if(index<0) index = -1*(index+1); return index; } }
You are given an array nums of size n consisting of distinct integers from 1 to n and a positive integer k.
Return the number of non-empty subarrays in nums that have a median equal to k.
Note:
- The median of an array is the middle element after sorting the array in ascending order. If the array is of even length, the median is the left middle element.
- For example, the median of
[2,3,1,4]is2, and the median of[8,4,3,5,1]is4.
- For example, the median of
- A subarray is a contiguous part of an array.
Example 1:
Input: nums = [3,2,1,4,5], k = 4 Output: 3 Explanation: The subarrays that have a median equal to 4 are: [4], [4,5] and [1,4,5].
Example 2:
Input: nums = [2,3,1], k = 3 Output: 1 Explanation: [3] is the only subarray that has a median equal to 3.
Constraints:
n == nums.length1 <= n <= 1051 <= nums[i], k <= n- The integers in
numsare distinct.
解法：
1.找到k的位置
2.从k开始向右遍历，balance统计大于/小于k的个数，并记录到map
3.从k开始向左遍历，balance统计大于/小于k的个数并match 左侧map中的count
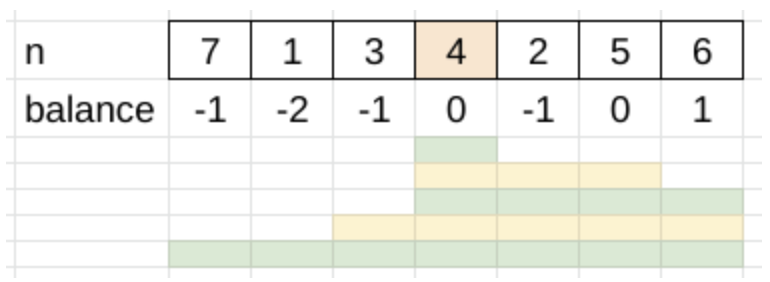
class Solution { public int countSubarrays(int[] nums, int k) { int pos = 0; //找到k的位置 for(int i = 0; i < nums.length; i++) { if(nums[i] == k){ pos = i; break; } } Map<Integer, Integer> map = new HashMap(); //从pos向右👉计算balance并记录统计个数 int balance = 0; for(int i = pos; i < nums.length; i++){ if(nums[i] > k) { balance++; } else if(nums[i] < k){ balance--; } map.put(balance, map.getOrDefault(balance, 0) + 1); } //从pos向左👈计算balance，与左侧记录的个数进行match balance = 0; int cnt = 0; for(int i = pos; i >= 0; i--){ if(nums[i] > k){ balance++; } else{ balance--; } cnt += map.getOrDefault(-1 * balance, 0) + map.getOrDefault(-1 * balance - 1, 0); } return cnt; } }
class Solution { public int countSubarrays(int[] nums, int k) { Map<Integer, Integer> map = new HashMap(); int balance = 0; int cnt = 0; map.put(0, 1); boolean flag = false; for(int num : nums){ if(num > k) balance++; else if(num < k) balance--; else flag = true; //k左边的数字，进行统计 if(flag){ cnt += map.getOrDefault(balance, 0) + map.getOrDefault(balance - 1, 0); } //k右边的数字，计算 else map.put(balance, map.getOrDefault(balance, 0) + 1); } return cnt; } }
You are given a 0-indexed integer array nums. There exists an array arr of length nums.length, where arr[i] is the sum of |i - j| over all j such that nums[j] == nums[i] and j != i. If there is no such j, set arr[i] to be 0.
Return the array arr.
Example 1:
Input: nums = [1,3,1,1,2] Output: [5,0,3,4,0] Explanation: When i = 0, nums[0] == nums[2] and nums[0] == nums[3]. Therefore, arr[0] = |0 - 2| + |0 - 3| = 5. When i = 1, arr[1] = 0 because there is no other index with value 3. When i = 2, nums[2] == nums[0] and nums[2] == nums[3]. Therefore, arr[2] = |2 - 0| + |2 - 3| = 3. When i = 3, nums[3] == nums[0] and nums[3] == nums[2]. Therefore, arr[3] = |3 - 0| + |3 - 2| = 4. When i = 4, arr[4] = 0 because there is no other index with value 2.
Example 2:
Input: nums = [0,5,3] Output: [0,0,0] Explanation: Since each element in nums is distinct, arr[i] = 0 for all i.
Constraints:
1 <= nums.length <= 1050 <= nums[i] <= 109
class Solution { public long[] distance(int[] nums) { Map<Integer, List<Integer>> map = new HashMap(); for(int i = 0; i < nums.length; i++) { List<Integer> list = map.getOrDefault(nums[i], new ArrayList()); list.add(i); map.put(nums[i], list); } long[] result = new long[nums.length]; for(int key : map.keySet()) { calculate(map.get(key), result); } return result; } private void calculate(List<Integer> list, long[] result) { int len = list.size(); //提前计算后缀和 long[] rightSum = new long[len]; rightSum[len - 1] = list.get(len - 1); for(int i = len - 2; i >= 0; i--) { rightSum[i] = list.get(i) + rightSum[i + 1]; } long leftSum = 0; for(int i = 0; i < len; i++) { int curr = list.get(i); if(i < len - 1) //计算当前元素与它后面元素的差值之和，即为：后面所有元素之和-当前元素*后面元素个数 取绝对值 result[curr] = Math.abs(rightSum[i + 1] - (long)curr * (len - i -1)); //计算当前元素与它前面元素差值这和，即为：前面所有元素之和-当前元素*后面元素个数 取绝对值 result[curr] += Math.abs(leftSum - (long)curr * i); leftSum += list.get(i); } } }
You are given a 0-indexed integer array nums and a positive integer k.
You can apply the following operation on the array any number of times:
- Choose any subarray of size
kfrom the array and decrease all its elements by1.
Return true if you can make all the array elements equal to 0, or false otherwise.
A subarray is a contiguous non-empty part of an array.
Example 1:
Input: nums = [2,2,3,1,1,0], k = 3 Output: true Explanation: We can do the following operations: - Choose the subarray [2,2,3]. The resulting array will be nums = [1,1,2,1,1,0]. - Choose the subarray [2,1,1]. The resulting array will be nums = [1,1,1,0,0,0]. - Choose the subarray [1,1,1]. The resulting array will be nums = [0,0,0,0,0,0].
Example 2:
Input: nums = [1,3,1,1], k = 2 Output: false Explanation: It is not possible to make all the array elements equal to 0.
Constraints:
1 <= k <= nums.length <= 1050 <= nums[i] <= 106
解法： 这个题跟370题很像
class Solution: def checkArray(self, nums: List[int], k: int) -> bool: diff = [0] * len(nums) prefixSum = 0 for i in range(0, len(nums)): #计算prefix Sum prefixSum += diff[i] #如果当前已经大于目标位置值，那么不满足 if prefixSum > nums[i]: return False #如果已经不够窗口长度，没法再操作，只需要判定是否于目标值相等 if i > len(nums) - k: if nums[i] != prefixSum: return False #如果不够，那么在接下来k的窗口增加 if nums[i] > prefixSum: add = nums[i] - prefixSum diff[i] += add if i + k < len(nums): diff[i + k] -= add prefixSum = nums[i] return True
Given a 2D character matrix grid, where grid[i][j] is either 'X', 'Y', or '.', return the number of submatrices
grid[0][0]- an equal frequency of
'X'and'Y'. - at least one
'X'.
Example 1:
Input: grid = [["X","Y","."],["Y",".","."]]
Output: 3
Explanation:
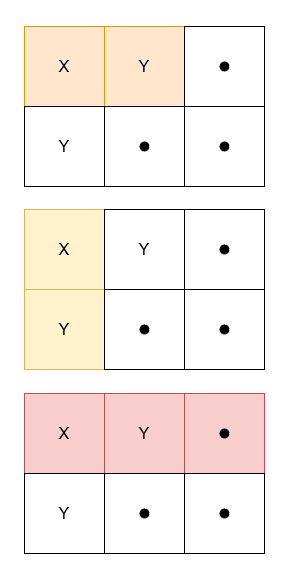
Example 2:
Input: grid = [["X","X"],["X","Y"]]
Output: 0
Explanation:
No submatrix has an equal frequency of 'X' and 'Y'.
Example 3:
Input: grid = [[".","."],[".","."]]
Output: 0
Explanation:
No submatrix has at least one 'X'.
Constraints:
1 <= grid.length, grid[i].length <= 1000grid[i][j]is either'X','Y', or'.'.
class Solution { public int numberOfSubmatrices(char[][] grid) { int m = grid.length, n = grid[0].length; int result = 0; Count[][] count = new Count[m + 1][n + 1]; for(int i = 0; i <= m; i++) count[i][0] = new Count(0, 0); for(int i = 0; i <= n; i++) count[0][i] = new Count(0, 0); for(int i = 0; i < m; i++) { for(int j = 0; j < n; j++) { int x = grid[i][j] == 'X' ? 1 : 0; int y = grid[i][j] == 'Y' ? 1 : 0; x += count[i + 1][j].x + count[i][j + 1].x - count[i][j].x; y += count[i + 1][j].y + count[i][j + 1].y - count[i][j].y; count[i + 1][j + 1] = new Count(x, y); if(x > 0 && x == y) result++; } } return result; } record Count(int x, int y){} }
You are given a 0-indexed 2D integer array flowers, where flowers[i] = [starti, endi] means the ith flower will be in full bloom from starti to endi (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the ith person will arrive to see the flowers.
Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the ith person arrives.
Example 1:
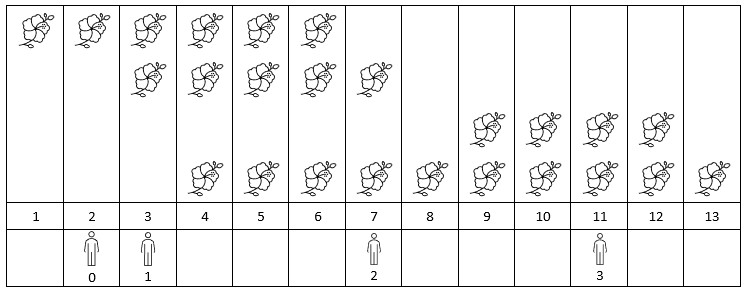
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11] Output: [1,2,2,2] Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive. For each person, we return the number of flowers in full bloom during their arrival.
Example 2:
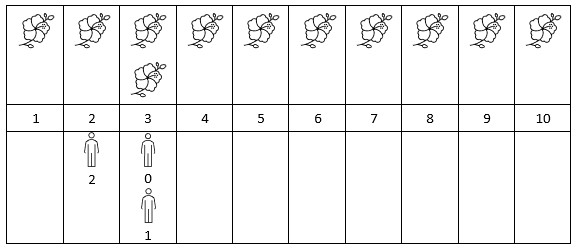
Input: flowers = [[1,10],[3,3]], people = [3,3,2] Output: [2,2,1] Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive. For each person, we return the number of flowers in full bloom during their arrival.
Constraints:
1 <= flowers.length <= 5 * 104flowers[i].length == 21 <= starti <= endi <= 1091 <= people.length <= 5 * 1041 <= people[i] <= 109
思路： 扫描线+前缀和+二分搜索
class Solution { record TimeLine(int t, int count){} public int[] fullBloomFlowers(int[][] flowers, int[] people) { // 生成扫描线 List<int[]> scanLine = getScanLine(flowers); // 遍历扫描线做prefix sum，生成所有start，end时间的开花数 List<TimeLine> tlist = new ArrayList<>(); int curr = 0; for (int[] pair : scanLine) { curr += pair[1]; tlist.add(new TimeLine(pair[0], curr)); } int[] result = new int[people.length]; for (int i = 0; i < people.length; i++) { // 二分法求某天的开花数 result[i] = bs(tlist, people[i]); } return result; } // 二分搜索某天的开花数 private int bs(List<TimeLine> list, int target) { int left = 0, right = list.size() - 1; int result = 0; while(left <= right) { int mid = left + (right - left) / 2; if(list.get(mid).t <= target) { result = list.get(mid).count; left = mid + 1; } else { right = mid - 1; } } return result; } private List<int[]> getScanLine(int[][] flowers) { // sort : asc(time), asc(flag) List<int[]> list = new ArrayList<>(); for (int[] flower : flowers) { list.add(new int[]{flower[0], 1}); list.add(new int[]{flower[1] + 1, -1}); //关键点就在这个位置 } Collections.sort(list, (x, y) -> { if(x[0] == y[0]) return y[1] - x[1]; return x[0] - y[0]; }); return list; } } /** [1,6],[3,7],[4,13],[9,12]
扫描线： 1,1 3,1 4,1 7,-1 8,-1 9,1 13,-1 14,-1
prefixsum, 到每个时间点的开花数： 1,1 3,2 4,3 7,2 8,1 9,2 13,1 14,0 */
You are given an array of integers nums and an integer k.
Return the maximum sum of a non-empty subarray of nums, such that the size of the subarray is divisible by k.
A subarray is a contiguous non-empty sequence of elements within an array.
Example 1:
Input: nums = [1,2], k = 1
Output: 3
Explanation:
The subarray [1, 2] with sum 3 has length equal to 2 which is divisible by 1.
Example 2:
Input: nums = [-1,-2,-3,-4,-5], k = 4
Output: -10
Explanation:
The maximum sum subarray is [-1, -2, -3, -4] which has length equal to 4 which is divisible by 4.
Example 3:
Input: nums = [-5,1,2,-3,4], k = 2
Output: 4
Explanation:
The maximum sum subarray is [1, 2, -3, 4] which has length equal to 4 which is divisible by 2.
Constraints:
1 <= k <= nums.length <= 2 * 105-109 <= nums[i] <= 109
class Solution { /** 思路： prefixsum + k map<sortedSet>(用于存储每个位置取模后的prefixsum) */ public long maxSubarraySum(int[] nums, int k) { // 定义map存储prefixsum的值 TreeSet<Long>[] arr = new TreeSet[k]; for(int i = 0; i < k; i++) { arr[i] = new TreeSet<Long>(); } // 求去prefixsum long result = Long.MIN_VALUE; // 空的时候需要有一个占位插进去, 比如第k个元素(下标k-1)的时候已经够k个了 arr[k - 1].add(0l); long sum = 0; for(int i = 0; i < nums.length; i++) { sum += nums[i]; int pos = i % k; // 如果数量还不够k个，记录prefixsum然后返回 if(i < k - 1) { arr[pos].add(sum); continue; } result = Math.max(result, sum - arr[pos].first()); arr[pos].add(sum); } return result; } } /* 0 1 2 3 4 -5, 1, 2,-3, 4 -5 -4 -2 -5 -1 i -1:0 0:-5,-1 1:-4 2:-2 3:-5 */
points, where points[i] = [xi, yi] represents the coordinates of the ith point on the Cartesian plane.A horizontal trapezoid is a convex quadrilateral with at least one pair of horizontal sides (i.e. parallel to the x-axis). Two lines are parallel if and only if they have the same slope.
Return the number of unique horizontal trapezoids that can be formed by choosing any four distinct points from points.
Since the answer may be very large, return it modulo 109 + 7.
Example 1:
Input: points = [[1,0],[2,0],[3,0],[2,2],[3,2]]
Output: 3
Explanation:
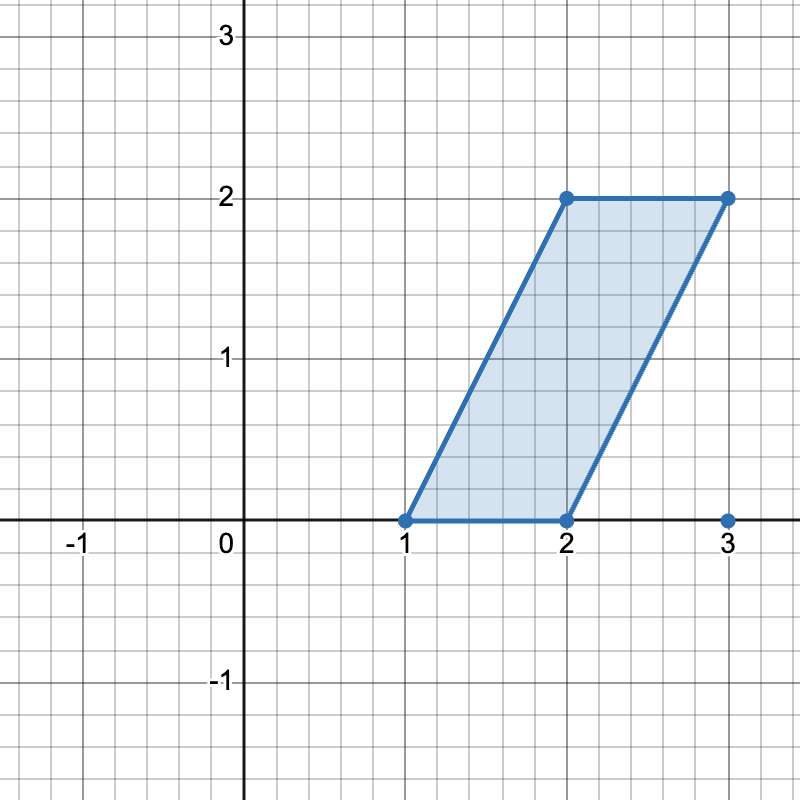
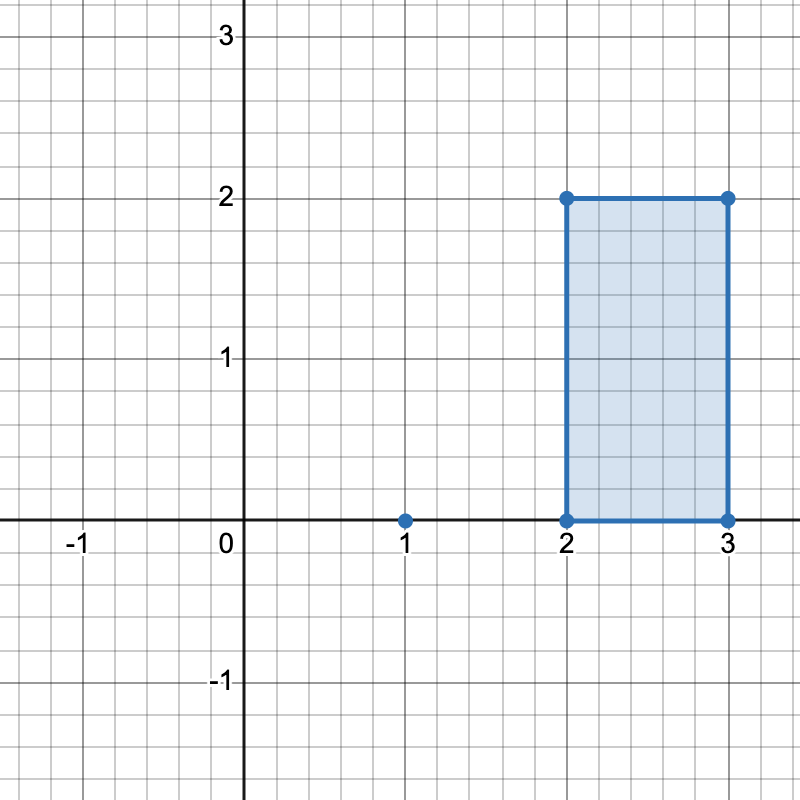
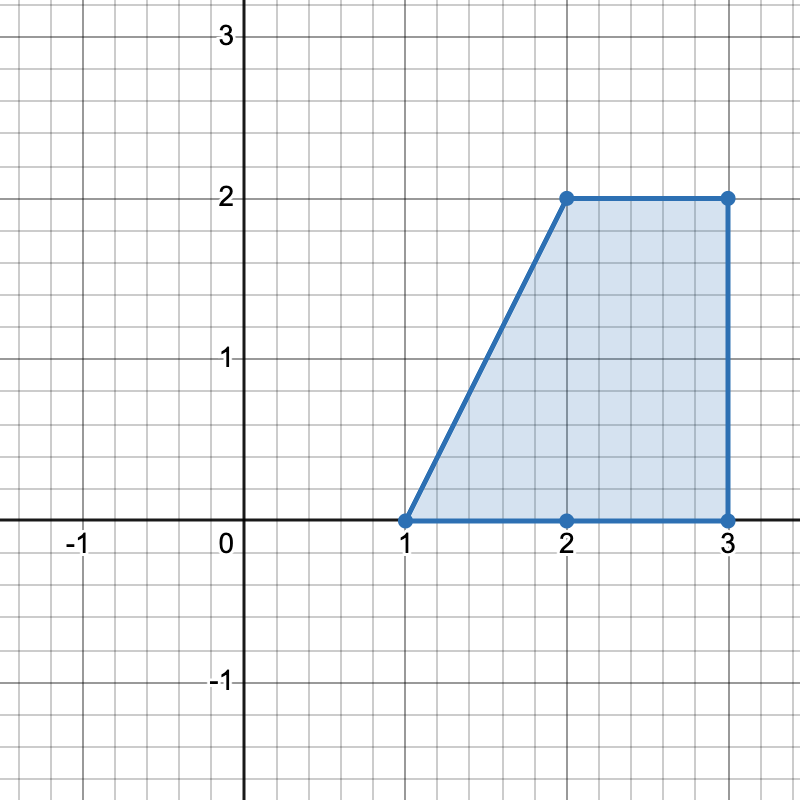
There are three distinct ways to pick four points that form a horizontal trapezoid:
- Using points
[1,0],[2,0],[3,2], and[2,2]. - Using points
[2,0],[3,0],[3,2], and[2,2]. - Using points
[1,0],[3,0],[3,2], and[2,2].
Example 2:
Input: points = [[0,0],[1,0],[0,1],[2,1]]
Output: 1
Explanation:
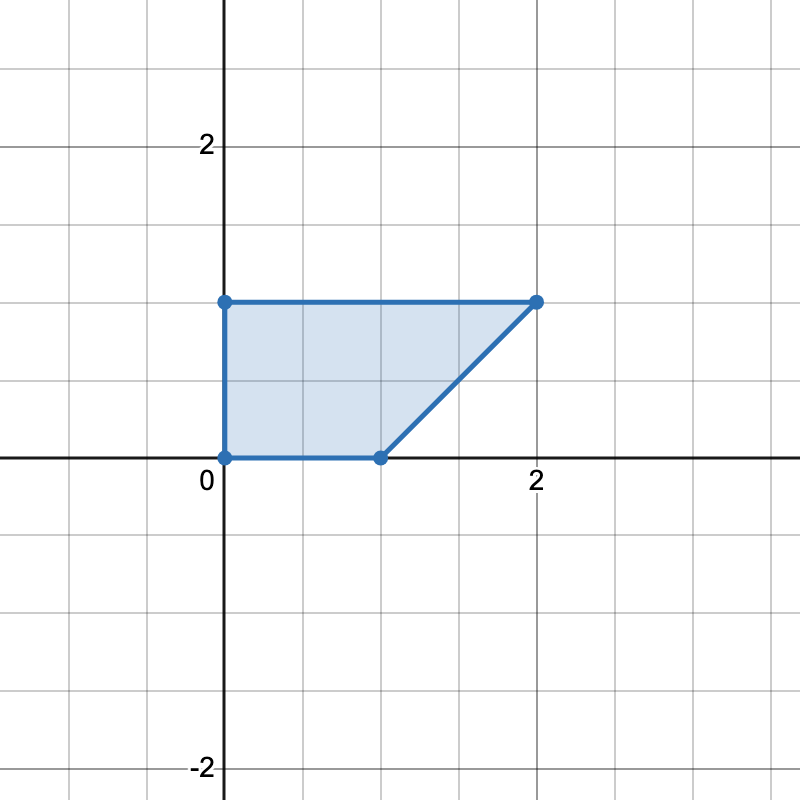
There is only one horizontal trapezoid that can be formed.
Constraints:
4 <= points.length <= 105–108 <= xi, yi <= 108- All points are pairwise distinct.
class Solution: def countTrapezoids(self, points: List[List[int]]) -> int: K = 1000000007 maps = {} for x, y in points: maps[y] = (maps.get(y, 0) + 1) % K for k, v in maps.items(): # v个元素中抽取2个的抽法 maps[k] = v * (v - 1) // 2 total = 0 # 当前组合总数量 result = 0 for k, val in maps.items(): result += total * val result %= K total += val # 将当前行的组合数量加到总数量中 return result%K
s consisting only of the characters 'a', 'b', and 'c'.A of s is called balanced if all distinct characters in the substring appear the same number of times.
Return the length of the longest balanced substring of s.
Example 1:
Input: s = "abbac"
Output: 4
Explanation:
The longest balanced substring is "abba" because both distinct characters 'a' and 'b' each appear exactly 2 times.
Example 2:
Input: s = "aabcc"
Output: 3
Explanation:
The longest balanced substring is "abc" because all distinct characters 'a', 'b' and 'c' each appear exactly 1 time.
Example 3:
Input: s = "aba"
Output: 2
Explanation:
One of the longest balanced substrings is "ab" because both distinct characters 'a' and 'b' each appear exactly 1 time. Another longest balanced substring is "ba".
Constraints:
1 <= s.length <= 105scontains only the characters'a','b', and'c'.
''' 首先，分3种情况： res1：最长连续相同字符子串。 res2：按某些“主导字符”拆分后，各子串中的最长平衡段。 ab,ac,bc res3：通用情况（所有字符参与）。 abc 其次，对于res2和res3两种，我们使用频率差的前缀和进行计算 ''' class Solution: def longestBalanced(self, s: str) -> int: def test(s): # 计算各个字符跟第一个字符的频率差 def diff(): return tuple(count[c] - count[chs[0]] for c in chs) # s中字符剔重 chs = list(set(s)) # 定义Counter count = Counter() # 前缀和初始化为0 pos = {diff(): -1} res = 0 for i, c in enumerate(s): # 更新字符count count[c] += 1 # 计算频率差 d = diff() # 如果出现过相同的频率差，那么就找到了符合条件的结果 if d in pos: res = max(res, i - pos[d]) # 如果没有的话，加进来 else: pos[d] = i return res # 单个字符情况考虑,找出连续最长的单个字符长度 # 这里groupby会统计每段"连续相同字符"的长度 res1 = max(len(list(it)) for c, it in groupby(s)) # 两个字符的情况考虑 # 按照 a, b, c对字符串进行切分，分别计算 ab, ac, bc 的最大balance长度 res2 = max(test(s2) for c in 'abc' for s2 in s.split(c)) # 3个字符的情况考虑 res3 = test(s) return max(res1, res2, res3)
浙公网安备 33010602011771号