经典考题二数岛屿

200. Number of Islands

Medium

Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands.

An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1:

Input: grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
Output: 1

Example 2:

Input: grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
Output: 3

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] is '0' or '1'.

DFS

class Solution {
    public int numIslands(char[][] grid) {
        int count = 0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j]=='1') {
                    dfs(grid,i,j);
                    count++;
                }
            }
        }
        return count;
    }
    private void dfs(char[][] grid,int x,int y){
        if(x<0||x>=grid.length||y<0||y>=grid[0].length ) return;
        if(grid[x][y]=='0') return;
        grid[x][y]='0';
        int[][] directions = new int[][]{{-1,0},{1,0},{0,-1},{0,1}};
        for(int[] direct : directions){
            dfs(grid,x+direct[0],y+direct[1]);
        }
    }
}

BFS

class Solution {
    public int numIslands(char[][] grid) {
        int count = 0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j]=='1') {
                    bfs(grid,i,j);
                    count++;
                }
            }
        }
        return count;
    }
    private void bfs(char[][] grid,int x,int y){
        Queue<int[]> queue = new LinkedList();
        int[][] directions = new int[][]{{-1,0},{1,0},{0,-1},{0,1}};
        grid[x][y]='0';
        queue.offer(new int[]{x,y});
        while(!queue.isEmpty()){
            int[] pos = queue.poll();
            for(int[] direct:directions){
                int xx = pos[0]+direct[0];
                int yy = pos[1]+direct[1];
                if(xx>=0 && xx<grid.length && yy>=0 && yy<grid[0].length && grid[xx][yy]=='1'){
                    grid[xx][yy]='0';
                    queue.offer(new int[]{xx,yy});
                }
            }
        }
    }
}

时间复杂度：O(MN)

860 · Number of Distinct Islands

Algorithms

Medium

Description

Given a non-empty 2D array grid of 0's and 1's, an island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical). You may assume all four edges of the grid are surrounded by water.

Count the number of distinct islands. An island is considered to be the same as another if and only if one island has the same shape as another island (and not rotated or reflected).

Notice that:

11
1

and

 1
11

are considered different island, because we do not consider reflection / rotation.

The length of each dimension in the given grid does not exceed 50.

Example

Example 1:

Input: 
  [
    [1,1,0,0,1],
    [1,0,0,0,0],
    [1,1,0,0,1],
    [0,1,0,1,1]
  ]
Output: 3
Explanation:
  11   1    1
  1        11   
  11
   1

Example 2:

Input:
  [
    [1,1,0,0,0],
    [1,1,0,0,0],
    [0,0,0,1,1],
    [0,0,0,1,1]
  ]
Output: 1
解法，只需要在dfs基础上增加path去跟踪遍历路径，如果遍历路径相同的即为同样形状的岛屿

public class Solution {
    public int numberofDistinctIslands(int[][] grid) {
        if(grid==null || grid.length==0) return 0;
        Set<String> set = new HashSet();
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j]==1) {
                    path="";
                    dfs(grid,i,j,"start");
                    set.add(path);
                }
            }
        }
        return set.size();
    }
    private String path = "";
    private void dfs(int[][] grid,int x,int y,String direct){
        path+=direct+"#";
        if(x<0 || x>=grid.length || y<0 || y>=grid[0].length || grid[x][y]==0 ) {
            return;
        }
        grid[x][y] = 0;
        dfs(grid,x-1,y,"l");
        dfs(grid,x+1,y,"r");
        dfs(grid,x,y-1,"u");
        dfs(grid,x,y+1,"d");
    }
}

时间复杂度：O(MN)

434 · Number of Islands II

Algorithms

Medium

Description

Given a n,m which means the row and column of the 2D matrix and an array of pair A( size k). Originally, the 2D matrix is all 0 which means there is only sea in the matrix. The list pair has k operator and each operator has two integer A[i].x, A[i].y means that you can change the grid matrix[A[i].x][A[i].y] from sea to island. Return how many island are there in the matrix after each operator.You need to return an array of size K.

0 is represented as the sea, 1 is represented as the island. If two 1 is adjacent, we consider them in the same island. We only consider up/down/left/right adjacent.

Example

Example 1:

Input: n = 4, m = 5, A = [[1,1],[0,1],[3,3],[3,4]]
Output: [1,1,2,2]
Explanation:
0.  00000
    00000
    00000
    00000
1.  00000
    01000
    00000
    00000
2.  01000
    01000
    00000
    00000
3.  01000
    01000
    00000
    00010
4.  01000
    01000
    00000
    00011

Example 2:

Input: n = 3, m = 3, A = [[0,0],[0,1],[2,2],[2,1]]
Output: [1,1,2,2]

/**
 * Definition for a point.
 * class Point {
 *     int x;
 *     int y;
 *     Point() { x = 0; y = 0; }
 *     Point(int a, int b) { x = a; y = b; }
 * }
 */

public class Solution {
    public List<Integer> numIslands2(int n, int m, Point[] operators) {
        UnionFind uf = new UnionFind(n*m);
        List<Integer> result = new ArrayList();
        if(operators==null ) return result;
        int[][] directions = new int[][]{{-1,0},{1,0},{0,-1},{0,1}};
        int count = 0;
        boolean[][] visited = new boolean[n][m];
        for(Point p:operators){
            if(!visited[p.x][p.y]){//坑点1:operators中的Point可能为重复元素
                count++;//每次遇到新元素先+1
                visited[p.x][p.y]=true;
                for(int[] direct:directions){
                    int xx = p.x+direct[0];
                    int yy = p.y+direct[1];
                    if(xx>=0 && xx<n && yy>=0 && yy<m && visited[xx][yy]){
                        if(uf.findParent(xx*m+yy)!=uf.findParent(p.x*m+p.y)){ //只有未连通的情况下，才执行连接
                            uf.union(xx*m+yy,p.x*m+p.y);
                            count--;//每次连通后都-1
                        }
                    }
                }
            }
            result.add(count);
        }
        return result;
    }
    //要确保uf写的没有问题
    class UnionFind{
        int[] parent;
        UnionFind(int size){
            parent = new int[size];
            for(int i=0;i<size;i++) parent[i]=i;
        }
        int findParent(int x){
            if(parent[x]==x) return x;
            parent[x] = findParent(parent[x]);
            return parent[x];
        }
        void union(int x,int y){
            parent[x] = findParent(x);
            parent[y] = findParent(y);
            if(parent[x]==parent[y]) return;
            parent[parent[x]]=y;
        }
    }
}

时间复杂度：近似于O(MN)，因为我们认为UnionFind时间复杂度接近O(1)

934. Shortest Bridge

Medium

You are given an n x n binary matrix grid where 1 represents land and 0 represents water.

An island is a 4-directionally connected group of 1's not connected to any other 1's. There are exactly two islands in grid.

You may change 0's to 1's to connect the two islands to form one island.

Return the smallest number of 0's you must flip to connect the two islands.

Example 1:

Input: grid = [[0,1],[1,0]]
Output: 1

Example 2:

Input: grid = [[0,1,0],[0,0,0],[0,0,1]]
Output: 2

Example 3:

Input: grid = [[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]]
Output: 1

Constraints:

n == grid.length == grid[i].length
2 <= n <= 100
grid[i][j] is either 0 or 1.
There are exactly two islands in grid.

class Solution {
    public int shortestBridge(int[][] grid) {
        Queue<int[]> queue = new LinkedList();
        boolean flag = false;
        //dfs把第一个岛加入队列
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j]==1){
                    dfs(grid,i,j,queue);
                    flag=true;
                    break;//坑点，
                }
            }
            if(flag) break;//坑点，注意这里是两层循环，里层break后外层也要break
        }

        //从第一个岛的节点开始做bfs，直至碰到第二个岛的点（即值为1的点）
        int step = 0;
        int[][] directions = new int[][]{{-1,0},{1,0},{0,-1},{0,1}};
        while(!queue.isEmpty()){
            int size = queue.size();
            for(int i=0;i<size;i++){
                int[] pos = queue.poll();
                for(int[] direct:directions){
                    int x = pos[0]+direct[0];
                    int y = pos[1]+direct[1];
                    if(x>=0&&x<grid.length&&y>=0&&y<grid[0].length){
                        if(grid[x][y]==1) return step;//如果bfs过程中碰到了1，那么说明已经发现了第二个岛
                        else if(grid[x][y]==0) {
                            grid[x][y]=-1;//访问过的节点置为-1
                            queue.offer(new int[]{x,y});
                        }
                    }
                }
            }
            step++;
        }
        return -1;
    }
    private void dfs(int[][] grid,int x,int y,Queue<int[]> queue){
        if(x<0||y<0||x>=grid.length||y>=grid[0].length||grid[x][y]!=1) return;
        grid[x][y]=-1;//访问过的节点置为-1
        queue.offer(new int[]{x,y});
        dfs(grid,x-1,y,queue);
        dfs(grid,x+1,y,queue);
        dfs(grid,x,y-1,queue);
        dfs(grid,x,y+1,queue);
    }
}

695. Max Area of Island

Medium

You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island in grid. If there is no island, return 0.

Example 1:

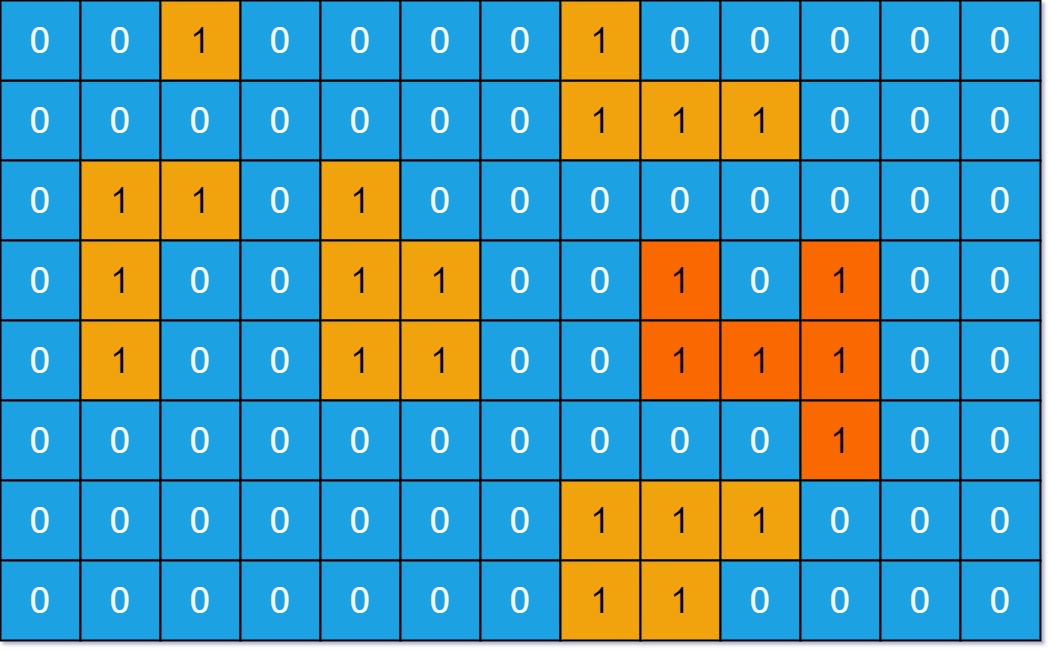
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6
Explanation: The answer is not 11, because the island must be connected 4-directionally.

Example 2:

Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] is either 0 or 1.

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int max = 0;
        for(int x=0;x<grid.length;x++){
            for(int y=0;y<grid[0].length;y++){
                count = 0;
                dfs(grid,x,y);
                max = Math.max(count,max);
            }
        }
        return max;
    }
    private int count = 0;
    private void dfs(int[][] grid,int x,int y){
        if(x<0||x>=grid.length||y<0||y>=grid[0].length) return;
        if(grid[x][y]==0) return;
        grid[x][y]=0;
        count++;
        int[][] directions = new int[][]{{-1,0},{1,0},{0,-1},{0,1}};
        for(int[] dir:directions){
            dfs(grid,x+dir[0],y+dir[1]);
        }
    }
}

463. Island Perimeter

Easy

You are given row x col grid representing a map where grid[i][j] = 1 represents land and grid[i][j] = 0 represents water.

Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).

The island doesn't have "lakes", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.

Example 1:

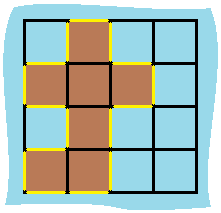
Input: grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
Output: 16
Explanation: The perimeter is the 16 yellow stripes in the image above.

Example 2:

Input: grid = [[1]]
Output: 4

Example 3:

Input: grid = [[1,0]]
Output: 4

Constraints:

row == grid.length
col == grid[i].length
1 <= row, col <= 100
grid[i][j] is 0 or 1.
There is exactly one island in grid.

解法一：

class Solution {
    public int islandPerimeter(int[][] grid) {
        int count = 0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j]==1) count+=dfs(grid,i,j);
            }
        }
        return count;
    }
    private int dfs(int[][] grid,int x,int y){
        if(x<0||x>=grid.length||y<0||y>=grid[0].length || grid[x][y]==0) return 1;
        if(grid[x][y]==-1) return 0;
        grid[x][y]=-1;
        return dfs(grid,x-1,y) + dfs(grid,x+1,y) + dfs(grid,x,y-1) + dfs(grid,x,y+1);
    }
}

解法二：

class Solution {
    /*
    逐行进行扫描
    1.遇到island 增加 4条边
    2.判断左边和上边是否有重合，一个重合减2条边
    */
    public int islandPerimeter(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int result = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                //如果不是island直接continue
                if(grid[i][j] == 0) continue;
                //每新增一个island增加4条边
                result += 4;
                //判断上面如果是island，重合减去2条边
                if(i > 0 && grid[i-1][j] == 1) result -= 2;
                //判断左面如果是island，重合减去2条边
                if(j > 0 && grid[i][j-1] == 1) result -= 2;
            }
        }
        return result;
    }
}

130. Surrounded Regions

Medium

Given an m x n matrix board containing 'X' and 'O', capture all regions that are 4-directionally surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Example 1:

Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
Explanation: Surrounded regions should not be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

Example 2:

Input: board = [["X"]]
Output: [["X"]]

Constraints:

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] is 'X' or 'O'.

class Solution {
    public void solve(char[][] board) {
        int m = board.length, n = board[0].length;
        //从4个周边为o的使用dfs找连通的O,找到的全部标记为T
        for(int x=0;x<m;x++){
            dfs(board,x,0,m,n);
            dfs(board,x,n-1,m,n);
        }
        for(int y=1;y<n-1;y++){
            dfs(board,0,y,m,n);
            dfs(board,m-1,y,m,n);
        }
        //把剩余的o全部标记为X，把标记为T的都改回到o
        for(int x=0;x<m;x++){
            for(int y=0;y<n;y++){
                if(board[x][y]=='O') board[x][y]='X';
                else if(board[x][y]=='T') board[x][y]='O';
            }
        }
    }
    public void dfs(char[][] board,int x,int y,int m,int n){
        if(x<0 || y<0|| x>=m||y>=n) return;
        if(board[x][y]=='X' || board[x][y]=='T' ) return;
        board[x][y]='T';
        dfs(board,x-1,y,m,n);
        dfs(board,x+1,y,m,n);
        dfs(board,x,y-1,m,n);
        dfs(board,x,y+1,m,n);
    }
}

1905. Count Sub Islands

Medium

You are given two m x n binary matrices grid1 and grid2 containing only 0's (representing water) and 1's (representing land). An island is a group of 1's connected 4-directionally (horizontal or vertical). Any cells outside of the grid are considered water cells.

An island in grid2 is considered a sub-island if there is an island in grid1 that contains all the cells that make up this island in grid2.

Return the number of islands in grid2 that are considered sub-islands.

Example 1:

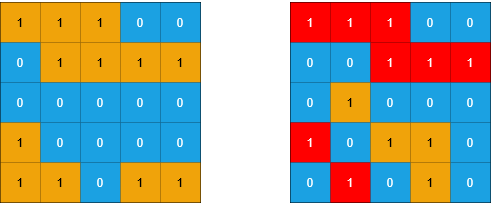
Input: grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
Output: 3
Explanation: In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.

Example 2:

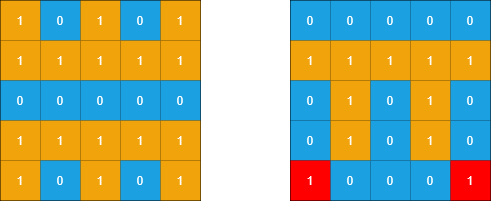
Input: grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
Output: 2 
Explanation: In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.

Constraints:

m == grid1.length == grid2.length
n == grid1[i].length == grid2[i].length
1 <= m, n <= 500
grid1[i][j] and grid2[i][j] are either 0 or 1.

class Solution {
    public int countSubIslands(int[][] grid1, int[][] grid2) {
        int count = 0;
        for(int i=0;i<grid2.length;i++){
            for(int j=0;j<grid2[0].length;j++){
                if( grid2[i][j]==1 && isSubIsland(grid1,grid2,i,j) ) count++;
            }
        }
        return count;
    }
    private boolean isSubIsland( int[][] grid1, int[][] grid2, int x, int y ){
        if(x<0 || x>=grid2.length || y<0 || y>=grid2[0].length || grid2[x][y]==0 ) return true;
        grid2[x][y] = 0;//遍历过的我们把它置0
        //这个地方必须把所有的方向都遍历完
        return isSubIsland(grid1,grid2,x-1,y) 
             & isSubIsland(grid1,grid2,x+1,y)
             & isSubIsland(grid1,grid2,x,y-1)
             & isSubIsland(grid1,grid2,x,y+1)
             & grid1[x][y]==1;  //如果grid1中不是岛那么不合法
    }
}

130. Surrounded Regions (M)	- 边缘开始连通，先标记为 #，再填回 X	邊緣兩次遍歷
200. Number of Islands (M)	- BFS / DFS / UF - 连通分量个数	小島數量
305. Number of Islands II (H)	- 岛一块一块长出，求输出任意时刻的岛屿数量 - UF 时刻检查连通分量个数	UF
419. Battleships in a Board (M)	- 同 200，代码可通过 - 最优解：可扫一遍	小島數量
463. Island Perimeter (E)	- 找小岛周围边数 - DFS 只要与边界，水相接的计入 - 最优解：直接扫描即可	小島邊界
694. Number of Distinct Islands (M)	- DFS / BFS - String path 纪录方向（东西南北），形状	小島形狀
695. Max Area of Island (M)	- DFS / BFS / UF - UF 找最大连通分量大小	小島大小
711. Number of Distinct Islands II (H)	- 694 旋转几个方向 - String path 纪录方向，形状，尝试八个方向旋转	小島形狀
827. Making A Large Island (H)	- 至多换一个 0 为 1，求最大岛屿 - UF - 基于 695最大岛屿，先找出各个岛屿大小 - 尝试任何一个可能 0，四个方向尝试连接成最大岛屿	小島大小 + UF
934. Shortest Bridge (M)	- 找到两个岛之间最短距离 (可以确定只有两个岛） - 先 DFS 标记一个岛为 2 - 再 BFS 从 2 开始走到任意 1 的最短距离，多源BFS - BFS + DFS 一起 - 多个岛屿怎么做？	先 DFS 再 BFS
1020. Number of Enclaves (M)	- 与边界相关的 1 不计，求内部有多少个 1 - 边缘为 1 的开始扩散往内，标成 0 - 再扫一遍计算有几个 1	邊緣兩次遍歷
1034. Coloring A Border (M)	- 找整个岛屿的最外一圈 - 找连通分量的边界 - BFS / DFS 判断是否是边界格子 - 四个方向都是同一个颜色，表示在内部，不是边界格子	小島邊界
1254. Number of Closed Islands (M)	- 找能够四周全被 1 包围的岛屿数量 - 边缘开始连通	邊緣小島數量兩次遍歷
1905. Count Sub Islands (M)	- 找被grid1全部包围，包含的子岛屿数量	小島數量兩次遍歷

posted @ 2021-12-08 10:12 xiaoyongyong 阅读(71) 评论(0) 收藏举报

xiaoyongyong

经典考题二 数岛屿

公告

经典考题二数岛屿