Tree 系列（四） LCA

236. Lowest Common Ancestor of a Binary Tree

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [1,2], p = 1, q = 2
Output: 1

Constraints:

The number of nodes in the tree is in the range [2, 105].
-109 <= Node.val <= 109
All Node.val are unique.
p != q
p and q will exist in the tree.

解法一

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null || root.val==p.val || root.val==q.val) return root;
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if(left!=null && right!=null) return root;
        if(left!=null) return left;
        if(right!=null) return right;
        return null;
    }
}

解法二

第一步 traversal 构建从孩子节点->父亲节点的关系

第二步从p q节点寻找共同的父节点

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    Map<TreeNode,TreeNode> map = new HashMap();
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        traversal(null,root);
        Set<TreeNode> pset = new HashSet();
        while(p!=null){
            pset.add(p);
            p = map.get(p);
        }
        while(q!=null){
            if(pset.contains(q)) return q;
            q = map.get(q);
        }
        return null;
    }
    public void traversal(TreeNode parent,TreeNode curr){
        if(curr==null) return;
        map.put(curr,parent);
        traversal(curr,curr.left);
        traversal(curr,curr.right);
    }
}

578 · Lowest Common Ancestor III （lintcode）

Given the root and two nodes in a Binary Tree. Find the lowest common ancestor(LCA) of the two nodes.

The nearest common ancestor of two nodes refers to the nearest common node among all the parent nodes of two nodes (including the two nodes).
Return null if LCA does not exist.

node A or node B may not exist in tree.
Each node has a different value

样例

Example1

Input: 
{4, 3, 7, #, #, 5, 6}
3 5
5 6
6 7 
5 8
Output: 
4
7
7
null
Explanation:
  4
 / \
3   7
   / \
  5   6

LCA(3, 5) = 4
LCA(5, 6) = 7
LCA(6, 7) = 7
LCA(5, 8) = null

解法： 这道题是上面那道题的升级版，我们可以在上面一道题的基础上进行改进
 1.为了确保两个节点都存在，可以增加一个全局变量count，每次匹配到的时候count++
 2.我们需要遍历所有节点，因此不能在匹配的时候立即返回，而是要遍历整个树的每个节点，因此可以改为后续遍历

/**
 * Definition of TreeNode:
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left, right;
 *     public TreeNode(int val) {
 *         this.val = val;
 *         this.left = this.right = null;
 *     }
 * }
 */
public class Solution {
    int count=0;
    public TreeNode lowestCommonAncestor3(TreeNode root, TreeNode A, TreeNode B) {
        TreeNode result  = helper(root,A,B);
        return count==2 ? result : null;
    }
    public TreeNode helper(TreeNode root, TreeNode A, TreeNode B) {
        if(root==null ) return null;
　　　　 //此处修改为后续遍历,确保子节点也遍历一遍计算count
        TreeNode left = helper(root.left,A,B);
        TreeNode right = helper(root.right,A,B);
        if(root.val == A.val || root.val == B.val) {
            count++;
            return root;
        }
        if(left!=null && right!=null) return root;
        if(left!=null) return left;
        if(right!=null) return right;
        return null;
    }
}

1650. Lowest Common Ancestor of a Binary Tree III

Description

Given two nodes of a binary tree p and q, return their lowest common ancestor (LCA).

Each node will have a reference to its parent node. The definition for Node is below:

class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

According to the definition of LCA on Wikipedia: "The lowest common ancestor of two nodes p and q in a tree T is the lowest node that has both p and q as descendants (where we allow a node to be a descendant of itself)."

Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5 since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [1,2], p = 1, q = 2
Output: 1

Constraints:

The number of nodes in the tree is in the range [2, 10⁵].
-10⁹ <= Node.val <= 10⁹
All Node.val are unique.
p != q
p and q exist in the tree.

Hints

Store the path from p to the root.
Traverse the path from q to the root, the first common point of the two paths is the LCA.

解法一：这个题换汤不换药，题目数据结构中还给出了我们当前节点和parent 之间的关系，直接上第一题中的解法二即可

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
};
*/

class Solution {
    public Node lowestCommonAncestor(Node p, Node q) {
        Set<Node> set = new HashSet();
        while(p!=null){
        　　set.add(p);
        　　p=p.parent;
    　　}
    　　while(q!=null){
        　　if(set.contains(q)) return q;
        　　q = q.parent;
    　　}
    　　return null;
    }
}

解法二：我们可以把求取这两个节点的共同parent 转换为求这两个节点出发的两个单向链表的交汇处

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
};
*/

class Solution {
    public Node lowestCommonAncestor(Node p, Node q) {
        Node orgp = p;
        Node orgq = q;
        while(p!=q){
            if(p.parent!=null) p = p.parent;
            else p = orgq;
            if(q.parent!=null) q = q.parent;
            eles q = orgp;
        }
        return p;
    }
}

1676. Lowest Common Ancestor of a Binary Tree IV

Given the root of a binary tree and an array of TreeNode objects nodes, return the lowest common ancestor (LCA) of all the nodes in nodes. All the nodes will exist in the tree, and all values of the tree's nodes are unique.

Extending the definition of LCA on Wikipedia: "The lowest common ancestor of n nodes p1, p2, ..., pn in a binary tree T is the lowest node that has every pi as a descendant (where we allow a node to be a descendant of itself) for every valid i". A descendant of a node x is a node y that is on the path from node x to some leaf node.

Example 1:

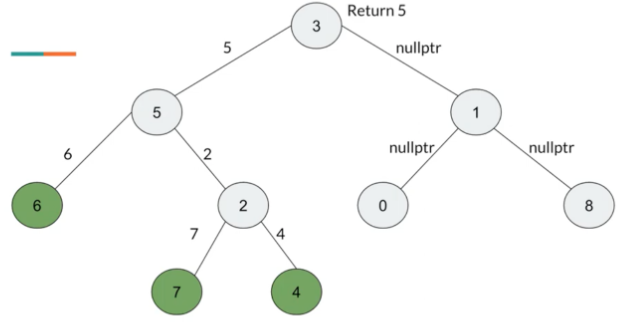
Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [4,7]
Output: 2
Explanation: The lowest common ancestor of nodes 4 and 7 is node 2.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [1]
Output: 1
Explanation: The lowest common ancestor of a single node is the node itself.

Example 3:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [7,6,2,4]
Output: 5
Explanation: The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.

Example 4:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [0,1,2,3,4,5,6,7,8]
Output: 3
Explanation: The lowest common ancestor of all the nodes is the root node.

Constraints:

The number of nodes in the tree is in the range [1, 104].
-109 <= Node.val <= 109
All Node.val are unique.
All nodes[i] will exist in the tree.
All nodes[i] are distinct.

解法：把目标节点扔到一个set里面，解法等同于第一题解法一，遍历节点时只要判定该元素存在于该set中（第一题中是该元素为p,q中一个），即返回该节点

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode[] nodes) {
        if (root == null || nodes == null || nodes.length == 0)
            return null;
        Set<TreeNode> set = new HashSet<TreeNode>();
        for (TreeNode node : nodes)
            set.add(node);
        return helper(root, set);
    }
    public TreeNode helper(TreeNode root, Set<TreeNode> set) {、
        if(root==null || set.contains(root)) return root;
        TreeNode left = helper(root.left,set);
        TreeNode right = helper(root.right,set);
        if(left!=null && right!=null) return root;
        if(left!=null) return left;
        if(right!=null) return right;
        return null;
    }
}

1123. Lowest Common Ancestor of Deepest Leaves

Given the root of a binary tree, return the lowest common ancestor of its deepest leaves.

Recall that:

The node of a binary tree is a leaf if and only if it has no children
The depth of the root of the tree is 0. if the depth of a node is d, the depth of each of its children is d + 1.
The lowest common ancestor of a set S of nodes, is the node A with the largest depth such that every node in S is in the subtree with root A.

Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest leaf-nodes of the tree.
Note that nodes 6, 0, and 8 are also leaf nodes, but the depth of them is 2, but the depth of nodes 7 and 4 is 3.

Example 2:

Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree, and it's the lca of itself.

Example 3:

Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest leaf node in the tree is 2, the lca of one node is itself.

Constraints:

The number of nodes in the tree will be in the range [1, 1000].
0 <= Node.val <= 1000
The values of the nodes in the tree are unique.

class Solution {
    public TreeNode lcaDeepestLeaves(TreeNode root) {
        //1.find the deepest node/nodes
        //2.find their common ancestor
        Dnode result = dfs(root,0);
        return result.node;
    }
    public Dnode dfs(TreeNode root,int deep){
        if(root==null) return null;        
        if(root.left==null && root.right==null) {
            System.out.println(root.val+"before new "+deep);        
            return new Dnode(root,deep);                          
        }
        else if(root.left==null) {
            return dfs(root.right,deep+1);
        }
        else if(root.right==null) {
            return dfs(root.left,deep+1);
        }
        else{
            Dnode right = dfs(root.right,deep+1);
            Dnode left = dfs(root.left,deep+1);
            System.out.println(left.deep+" "+right.deep);
            if(left.deep>right.deep) return left;
            else if(left.deep<right.deep) return right;
            else {
                return new Dnode(root,left.deep);
            }
        }
    }
    class Dnode{
        TreeNode node;
        int deep;
        Dnode(TreeNode node,int deep){
            this.node = node;
            this.deep = deep;
            System.out.println(node.val+" new "+deep);
        }
    }
}

class Solution {
    class DNode{
        TreeNode node;
        int depth;
        DNode(TreeNode node,int depth){
            this.node = node;
            this.depth = depth;
        }
    }
    public TreeNode lcaDeepestLeaves(TreeNode root) {
        DNode result  = helper(root,0);
        return result.node;
    }
    public DNode helper(TreeNode root,int depth){
        if(root==null) return new DNode(null,depth);
        DNode left = helper(root.left,depth+1);
        DNode right = helper(root.right,depth+1);
        if(left.depth>right.depth) return left;
        else if(left.depth<right.depth) return right;
        else return new DNode(root,left.depth);
    }
}

python:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def lcaDeepestLeaves(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        def dfs(curr):
            #如果为null直接返回
            if curr == None:
                return 0, None
            #分别计算左右子树
            left, leftResult = dfs(curr.left)
            right, rightReslt  = dfs(curr.right)
            #如果左右子树深度相同，那么返回当前节点
            if left == right:
                return left + 1, curr
            #不相同则分别返回左/右子树
            if left > right:
                return left + 1, leftResult
            if left < right:
                return right + 1, rightReslt
            
        return dfs(root)[1]

1372. Longest ZigZag Path in a Binary Tree

You are given the root of a binary tree.

A ZigZag path for a binary tree is defined as follow:

Choose any node in the binary tree and a direction (right or left).
If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
Change the direction from right to left or from left to right.
Repeat the second and third steps until you can't move in the tree.

Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).

Return the longest ZigZag path contained in that tree.

Example 1:

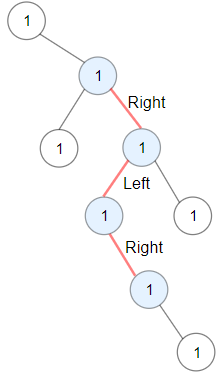
Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
Output: 3
Explanation: Longest ZigZag path in blue nodes (right -> left -> right).

Example 2:

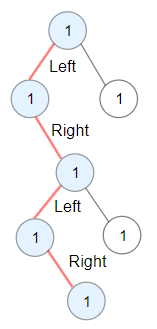
Input: root = [1,1,1,null,1,null,null,1,1,null,1]
Output: 4
Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).

Example 3:

Input: root = [1]
Output: 0

Constraints:

The number of nodes in the tree is in the range [1, 5 * 104].
1 <= Node.val <= 100

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int max = 0;
    public int longestZigZag(TreeNode root) {
        helper(root);
        return max-1;
    }
    public int[] helper(TreeNode root){
        int[] result  = new int[]{0,0};//[0]左侧SUM, [1]右侧SUM
        if(root==null) return result;
        int[] left = helper(root.left);
        int[] right = helper(root.right);
        result[0] = right[1]+1;
        result[1] = left[0]+1;
        max = Math.max(result[0],max);
        max = Math.max(result[1],max);
        return result;
    }
}

614 · 二叉树的最长连续子序列 II

描述

给定一棵二叉树，找到最长连续序列(单调且相邻节点值相差为1)路径的长度(节点数)。
路径起点跟终点可以为二叉树的任意节点。

样例

例1:

输入:
{1,2,0,3}
输出:
4
解释:
    1
   / \
  2   0
 /
3
0-1-2-3

例2:

输入:
{3,2,2}
输出:
2
解释:
    3
   / \
  2   2
2-3

/**
 * Definition of TreeNode:
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left, right;
 *     public TreeNode(int val) {
 *         this.val = val;
 *         this.left = this.right = null;
 *     }
 * }
 */

public class Solution {
    /**
     * @param root: the root of binary tree
     * @return: the length of the longest consecutive sequence path
     */
    int max = 0;
    public int longestConsecutive2(TreeNode root) {
        int[] result = helper(root);
        return max;
    }
    public int[] helper(TreeNode root){
        int[] result = new int[]{0,0}; //[0]表示升序 [1]表示降序
        if(root.left!=null){
            int[] left = helper(root.left);
            if(root.val+1==root.left.val) result[0]=left[0]+1;
            else if(root.val-1==root.left.val) result[1]=left[1]+1;
        }
        if(root.right!=null){
            int[] right = helper(root.right);
            if(root.val+1==root.right.val) result[0]=Math.max(right[0]+1,result[0]);
            if(root.val-1==root.right.val) result[1]=Math.max(right[1]+1,result[1]);
        }
        max = Math.max(result[0]+result[1]+1,max);
        return result;
    }
}

1373. Maximum Sum BST in Binary Tree

Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.

Example 1:

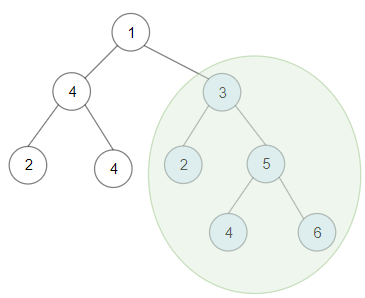
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

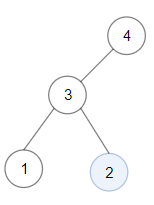
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Example 4:

Input: root = [2,1,3]
Output: 6

Example 5:

Input: root = [5,4,8,3,null,6,3]
Output: 7

Constraints:

The number of nodes in the tree is in the range [1, 4 * 104].
-4 * 104 <= Node.val <= 4 * 104

这个题的关键点在于： 1.是否为bst 2.获得最大的bst sum

当前子树是否为合法bst，取决于其子节点，而与其父节点没有任何关系，因此整个过程应该是自下而上的！

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int max=Integer.MIN_VALUE;
    public int maxSumBST(TreeNode node){
        helper(node);
        return max>=0 ? max : 0;
    }
    public int[] helper(TreeNode node){
        int[] result = new int[]{Integer.MAX_VALUE,Integer.MIN_VALUE,1,0};
        if(node==null) return result;//min,max,isValid,sum
        int[] left = helper(node.left);
        int[] right = helper(node.right);
        if(node.val>left[1] && node.val<right[0] && left[2]==1 && right[2]==1){
            result[3]= left[3]+right[3]+node.val;
            max = Math.max(max,result[3]);
            result[2]=1;
            result[0]=Math.min(left[0],node.val);
            result[1]=Math.max(right[1],node.val);
        }
        else{
            result[2]=0;
        }
        return result;
    }
}

129. Sum Root to Leaf Numbers

Medium

You are given the root of a binary tree containing digits from 0 to 9 only.

Each root-to-leaf path in the tree represents a number.

For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.

Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.

A leaf node is a node with no children.

Example 1:

Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

Example 2:

Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

Constraints:

The number of nodes in the tree is in the range [1, 1000].
0 <= Node.val <= 9
The depth of the tree will not exceed 10.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumNumbers(TreeNode root) {
        dfs(root,0);
        return sum;
    }
    int sum = 0;
    public void dfs(TreeNode root,int parent){
        if(root.left==null && root.right==null) sum+=parent*10+root.val;
        if(root.left!=null) dfs(root.left,root.val+parent*10);
        if(root.right!=null) dfs(root.right,root.val+parent*10);
    }
}

follow up: 如果是要求root到leaf的数字倒序相加呢？

比如：对下面的场景， sum = 21 + 31 = 52.

对下面场景：594+194+4=792

class Solution {
    public int sumNumbers(TreeNode root) {
        dfs(root,0,0);
        return sum;
    }
    int sum = 0;
    public void dfs(TreeNode root,int parent,int level){
        int curr = parent+root.val*Math.pow(10,level);
        if(root.left==null && root.right==null) sum+=curr;
        if(root.left!=null) dfs(root.left,curr,level+1);
        if(root.right!=null) dfs(root.right,curr,level+1);
    }
}

687. Longest Univalue Path

Medium

Given the root of a binary tree, return the length of the longest path, where each node in the path has the same value. This path may or may not pass through the root.

The length of the path between two nodes is represented by the number of edges between them.

Example 1:

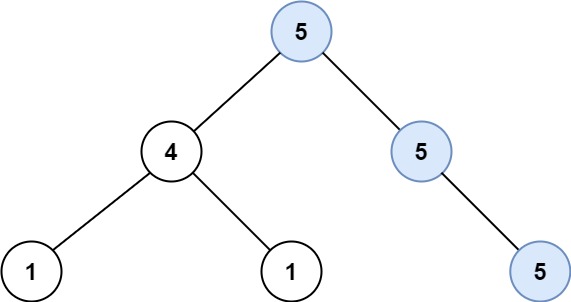
Input: root = [5,4,5,1,1,5]
Output: 2

Example 2:

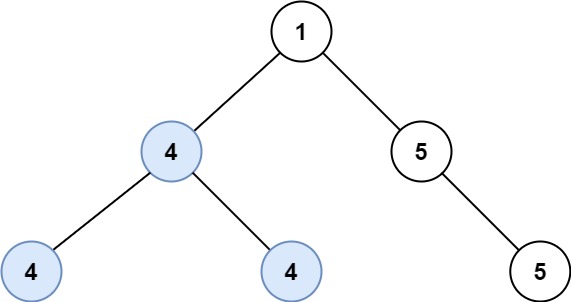
Input: root = [1,4,5,4,4,5]
Output: 2

Constraints:

The number of nodes in the tree is in the range [0, 104].
-1000 <= Node.val <= 1000
The depth of the tree will not exceed 1000.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int longestUnivaluePath(TreeNode root) {
        dfs(root,Integer.MAX_VALUE);
        return max;
    }
    private int max = 0;
    private int dfs(TreeNode root,int parent){
        if(root==null) return 0;
        int left = dfs(root.left,root.val);
        int right = dfs(root.right,root.val);
        max = Math.max(max,left+right);
        return root.val==parent ? Math.max(left,right)+1 : 0;
    }
}

366. Find Leaves of Binary Tree

Medium

Given the root of a binary tree, collect a tree's nodes as if you were doing this:

Collect all the leaf nodes.
Remove all the leaf nodes.
Repeat until the tree is empty.

Example 1:

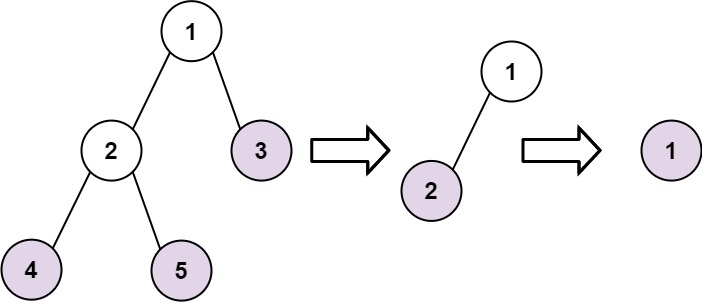
Input: root = [1,2,3,4,5]
Output: [[4,5,3],[2],[1]]
Explanation:
[[3,5,4],[2],[1]] and [[3,4,5],[2],[1]] are also considered correct answers since per each level it does not matter the order on which elements are returned.

Example 2:

Input: root = [1]
Output: [[1]]

Constraints:

The number of nodes in the tree is in the range [1, 100].
-100 <= Node.val <= 100

解法二：自上而下dfs遍历，自下而上postorder根据高度进行填充，时间复杂度O(N)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> findLeaves(TreeNode root) {
        List<List<Integer>> result = new ArrayList();
        getHeight(root, result);
        return result;
    }
    private int getHeight(TreeNode root, List<List<Integer>> result){
        //空节点认为高度为0
        if(root==null) return 0;
        //得到左右子树高度
        int left = getHeight(root.left, result);
        int right = getHeight(root.right, result);
        //当前高度为左右子树高度最大值+1
        int curr = Math.max(left,right)+1;
        //如果result中没有当前高度的集合，先创建加入
        if( curr >result.size() ) result.add(new ArrayList());
        //加入对应高度结果集
        result.get(curr-1).add(root.val);
        //返回当前高度
        return curr;
    }
}

2509. Cycle Length Queries in a Tree

Hard

You are given an integer n. There is a complete binary tree with 2n - 1 nodes. The root of that tree is the node with the value 1, and every node with a value val in the range [1, 2n - 1 - 1] has two children where:

The left node has the value 2 * val, and
The right node has the value 2 * val + 1.

You are also given a 2D integer array queries of length m, where queries[i] = [ai, bi]. For each query, solve the following problem:

Add an edge between the nodes with values ai and bi.
Find the length of the cycle in the graph.
Remove the added edge between nodes with values ai and bi.

Note that:

A cycle is a path that starts and ends at the same node, and each edge in the path is visited only once.
The length of a cycle is the number of edges visited in the cycle.
There could be multiple edges between two nodes in the tree after adding the edge of the query.

Return an array answer of length m where answer[i] is the answer to the ith query.

Example 1:

Input: n = 3, queries = [[5,3],[4,7],[2,3]]
Output: [4,5,3]
Explanation: The diagrams above show the tree of 23 - 1 nodes. Nodes colored in red describe the nodes in the cycle after adding the edge.
- After adding the edge between nodes 3 and 5, the graph contains a cycle of nodes [5,2,1,3]. Thus answer to the first query is 4. We delete the added edge and process the next query.
- After adding the edge between nodes 4 and 7, the graph contains a cycle of nodes [4,2,1,3,7]. Thus answer to the second query is 5. We delete the added edge and process the next query.
- After adding the edge between nodes 2 and 3, the graph contains a cycle of nodes [2,1,3]. Thus answer to the third query is 3. We delete the added edge.

Example 2:

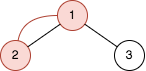
Input: n = 2, queries = [[1,2]]
Output: [2]
Explanation: The diagram above shows the tree of 22 - 1 nodes. Nodes colored in red describe the nodes in the cycle after adding the edge.
- After adding the edge between nodes 1 and 2, the graph contains a cycle of nodes [2,1]. Thus answer for the first query is 2. We delete the added edge.

Constraints:

2 <= n <= 30
m == queries.length
1 <= m <= 105
queries[i].length == 2
1 <= ai, bi <= 2n - 1
ai != bi

解法：这个题实际是求最低公共祖先，然后两者距离公共祖先距离+1 即为结果

class Solution {
    public int[] cycleLengthQueries(int n, int[][] queries) {
        int[] result = new int[queries.length];
        //
        for(int i = 0; i < queries.length; i++){
            //1.先遍历二者的祖先
            TreeMap<Integer,Integer> first = parents(queries[i][0]); //O(LogN)
            TreeMap<Integer,Integer> second = parents(queries[i][1]);//O(LogN)
            //2.再找出公共祖先并计算距离
            result[i] = dis(first, second);//O(LogN)
        }
        return result;
    }
    //求取二者的公共祖先得到距离
    private int dis(TreeMap<Integer,Integer> first, TreeMap<Integer, Integer> second){
        for(int num : first.keySet()){
            if(second.containsKey(num)) return first.get(num) + second.get(num) + 1;
        }
        return 0;
    }
    
    private TreeMap<Integer,Integer> parents(int n){
        TreeMap<Integer, Integer> map = new TreeMap<>((x,y) -> y - x);
        int i=0;
        while(n >= 1){
            map.put(n, i);
            i++;
            n /= 2;
        }
        return map;
    }
}

优秀解法：

    public int[] cycleLengthQueries(int n, int[][] queries) {
        int m = queries.length, res[] = new int[m];
        for (int i = 0; i < m; ++i) {
            res[i]++;
            int x = queries[i][0], y = queries[i][1];
            while (x != y) {
                if (x > y)
                    x /= 2;
                else
                    y /= 2;
                res[i]++;
            }
        }
        return res;
    }

posted @ 2021-09-30 11:14 xiaoyongyong 阅读(143) 评论(0) 收藏举报

xiaoyongyong

Tree 系列（四） LCA

1650. Lowest Common Ancestor of a Binary Tree III

Hints

1676. Lowest Common Ancestor of a Binary Tree IV

公告