Binary Search Tree 系列题目 98, 99, 96, 95, 450, 1008, 1373, 333,

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //两步走：
　　 //1.实现iterative方式的中序遍历
    //2.添加一个pre变量存放前一个元素val，在中序遍历过程中逐个判定是否递增
    public boolean isValidBST(TreeNode root) {
        if(root==null) return true;
        long pre = Long.MIN_VALUE;
        Stack<TreeNode> stack = new Stack();
        while(root!=null || !stack.isEmpty()){
            while(root!=null){
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if(root.val<=pre) return false;
            pre = root.val;
            root = root.right;
        }
        return true;
    }
}

 

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //recursive方式遍历，当前节点的左子树都应该小于该节点，右子树都应该大于该节点
    public boolean isValidBST(TreeNode root) {
        return helper(root,Long.MIN_VALUE,Long.MAX_VALUE);
    }
    public boolean helper(TreeNode root,long min,long max){
        if(root==null) return true;
        if(root.val<=min || root.val>=max) return false;
        return helper(root.left,min,root.val) && helper(root.right,root.val,max);
    }
}

 

173. Binary Search Tree Iterator

 实现一颗二叉树的iterator，这个肯定不适合用recursive的方式了，应该用iterative方式，如果熟悉iterative方式的二叉树中序遍历，那么这个题只是把遍历的步骤拆散了而已

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class BSTIterator {
    Stack<TreeNode> stack = new Stack();
    TreeNode curr;
    public BSTIterator(TreeNode root) {
        curr = root;
        // 初始化的时候将左侧节点都放入stack
        addAllLeft();
    }
    public int next() {
        // 去除栈顶
        curr = stack.pop();
        int val = curr.val;
        // 指向右子树
        curr = curr.right;
        addAllLeft();
        return val;
    }

    public boolean hasNext() {
        return !stack.isEmpty();
    }
    
    public void addAllLeft(){
        while(curr!=null){
            stack.push(curr);
            curr = curr.left;
        }
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator obj = new BSTIterator(root);
 * int param_1 = obj.next();
 * boolean param_2 = obj.hasNext();
 */

 

99. Recover Binary Search Tree

You are given the root of a binary search tree (BST), where the values of exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.

Example 1:

Input: root = [1,3,null,null,2]
Output: [3,1,null,null,2]
Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.

Example 2:

Input: root = [3,1,4,null,null,2]
Output: [2,1,4,null,null,3]
Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid. 

Constraints:

• The number of nodes in the tree is in the range [2, 1000].
• -231 <= Node.val <= 231 - 1

Follow up: A solution using O(n) space is pretty straight-forward. Could you devise a constant O(1) space solution?

 

 

/**

1,2,3,4,5

第一种情况2个逆序对

1,5,3,4,2
  x     y

第二种情况1个逆序对

1,2,3,5,4
      x y

*/

class Solution {
    public void recoverTree(TreeNode root) {
        TreeNode pre =null;
        TreeNode first = null;
        TreeNode second = null;
        Stack<TreeNode> stack = new Stack();
        //iteratively 遍历树，找到两个倒序的节点
        while(root!=null || !stack.isEmpty()){
            while(root!=null){
                stack.push(root);
                root=root.left;
            }
            root = stack.pop();
            if( pre!=null && pre.val>=root.val) {
                if(first==null) {
                    first = pre;
                    second = root; //tricky的地方
                }
                else {
                    second=root;
                    break;
                }
            }
            pre=root;
            root = root.right;
        }
　　　　//交换这两个元素的位置
        int temp = first.val;
        first.val = second.val;
        second.val = temp;
    }
}

 

 

96. Unique Binary Search Trees

Given an integer n, return the number of structurally unique BST's (binary search trees) which has exactly n nodes of unique values from 1 to n. 

Example 1:

Input: n = 3
Output: 5

Example 2:

Input: n = 1
Output: 1

Constraints:

• 1 <= n <= 19


 

class Solution {
    public int numTrees(int n) {
        return helper(n);
    }
    private int helper(int n) {
        // 个数为0或者1的时候，只有一种方式
        if(n == 1 || n == 0) return 1;
        int result = 0;
        for(int i = 1; i <= n; i++) {
            // 第i个元素为root的总数： 左侧方式 * 右侧方式
            result += helper(i - 1) * helper(n - i);
        }
        return result;
    }
}

加memoization

class Solution {
    public int numTrees(int n){
        int[] mem= new int[n+1];
        return numTrees(n,mem);
    }
    public int numTrees(int n,int[] mem) {
        if(n<0) return 0;
        if(n==0 || n==1) return 1;
        if(mem[n]!=0) return mem[n];

        for(int i=1;i<=n;i++){
            mem[n] += numTrees(i-1,mem)*numTrees(n-i,mem);
        }
        return mem[n];
    }
}

 

95. Unique Binary Search Trees II

Given an integer n, return all the structurally unique BST's (binary search trees), which has exactly n nodes of unique values from 1 to n. Return the answer in any order.

Example 1:

Input: n = 3
Output: [[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

Example 2:

Input: n = 1
Output: [[1]]

Constraints:

• 1 <= n <= 8

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<TreeNode> generateTrees(int n) {
        if(n==0) return new ArrayList();
        return helper(1,n);
    }
    public List<TreeNode> helper(int start,int end){
        List<TreeNode> list = new ArrayList();
        if(start>end) {
            list.add(null);
            return list;
        }
        for(int i=start;i<=end;i++){
            List<TreeNode> left = helper(start,i-1);
            List<TreeNode> right = helper(i+1,end);
            for(TreeNode lItem:left){
                for(TreeNode rItem:right){
                    TreeNode root = new TreeNode(i);
                    root.left = lItem;
                    root.right = rItem;
                    list.add(root);
                }
            }
        }
        return list;
    }
}

 

450. Delete Node in a BST

Medium

4691146Add to ListShare

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

1. Search for a node to remove.
2. If the node is found, delete the node.

 

Example 1:

Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.

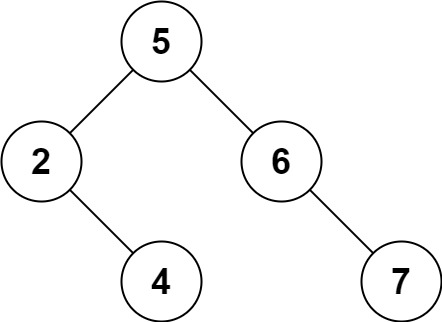
Example 2:

Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.

Example 3:

Input: root = [], key = 0
Output: []

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -105 <= Node.val <= 105
• Each node has a unique value.
• root is a valid binary search tree.
• -105 <= key <= 105

解法：

     0.目标位leaf node，直接return null

     1.目标的左子树为空，直接返回右子树

     2.目标的右子树为空，直接返回左子树

     3.左右子树都不为空， 删除左子树最大值节点，然后将其值替换至目标节点

 

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key){
        if(root==null) return null;
        //如果当前root为要删除的节点
        if(root.val==key){
            //如果是个叶子节点，直接返回null指向其父节点即可
            if(root.left==null && root.right==null) return null;
            //如果left为null，直接返回right
            else if(root.left==null) return root.right;
            //如果right为null，直接返回left
            else if(root.right==null) return root.left;
            //如果left,right都不为null， 2.
            else{
                //1.选择右子树最小值
                int swap = find(root.right);
                //2.将该值放到当前节点
                root.val=swap;
                //3.删除最小值所在节点
                root.right=deleteNode(root.right,swap);
            }
        }
        //如果target小于当前val，只需去左子树
        else if(key<root.val) root.left = deleteNode(root.left,key);
        //如果target大于当前val，只需去右子树
        else root.right = deleteNode(root.right,key);
        return root;
    }
    private int find(TreeNode root){
        while(root.left!=null) root=root.left;
        return root.val;
    }
}

 

1008. Construct Binary Search Tree from Preorder Traversal

Medium

Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.

It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.

A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.

A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.

 Example 1:

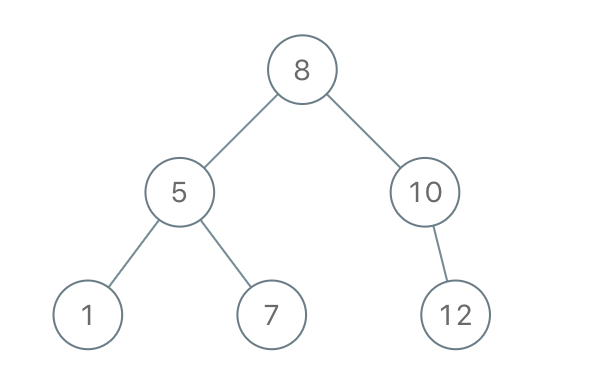
Input: preorder = [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]

Example 2:

Input: preorder = [1,3]
Output: [1,null,3]

Constraints:

• 1 <= preorder.length <= 100
• 1 <= preorder[i] <= 1000
• All the values of preorder are unique.

解法1:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
        return build(preorder,Long.MAX_VALUE,Long.MIN_VALUE);
    }
    private int index=0;
    private TreeNode build(int[] preorder,long max,long min){
        if(index>=preorder.length) return null;
        if(preorder[index]<=min || preorder[index]>=max) return null;
        TreeNode root = new TreeNode(preorder[index++]);
        root.left = build(preorder,root.val,min);
        root.right = build(preorder,max,root.val);
        return root;
    }
}

解法2:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
        return build( preorder, 0, preorder.length-1 );
    }
    private TreeNode build( int[] preorder, int left, int right ){
        if(left>right) return null;
        TreeNode root = new TreeNode(preorder[left]);
        if(left==right) return root;
        int rightind = right+1;
        for( rightind=left+1; rightind<=right; rightind++ ) if(preorder[rightind]>preorder[left]) break;
        root.left = build(preorder, left+1,Math.min(right,rightind-1));
        root.right = build(preorder, rightind,right);
        return root;
    }
}

  

1373. Maximum Sum BST in Binary Tree

Hard

Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees 

Example 1:

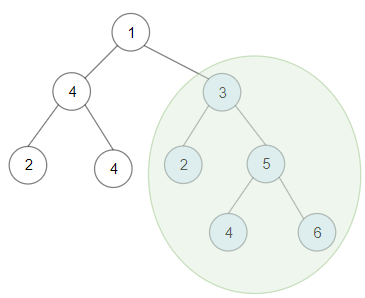
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

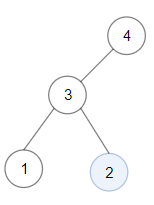
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Constraints:

• The number of nodes in the tree is in the range [1, 4 * 104].
• -4 * 104 <= Node.val <= 4 * 104

这个题关键点：

1.top-down很难判定下面的子树是否合法，因为如果上层已经不合法，因此我们要用bottomup

2.关键点就是 bottomup 如何判定整个子树是否合法bst

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    class Result{
        boolean isValid;//是否为合法bst
        int min,max,sum;//当前子树最大值，最小值，sum
        Result(boolean isValid,int min,int max,int sum){
            this.isValid = isValid;
            this.min = min;
            this.max = max;
            this.sum = sum;
        }
    }
    private int max = 0;
    public int maxSumBST(TreeNode root) {
        dfs(root);
        return max;
    }
    private Result dfs( TreeNode root ){
        //空节点认为是一个合法的bst,但是注意最大最小值的设置，这么设置MAX和MIN是避免叶子节点对该值的检查
        if(root==null) return new Result(true,Integer.MAX_VALUE,Integer.MIN_VALUE,0);//这个MAX_VALUE/MIN_VALUE使用非常巧妙
        //处理左右子树
        Result left = dfs(root.left);
        Result right = dfs(root.right);
        //如果左子树或右子树不满足，或者当前节点不满足，返回false
        if( !left.isValid || !right.isValid || root.val<=left.max || root.val>=right.min ) 
            return new Result(false,0,0,0);
        //如果是valid bst
        int sum = root.val + left.sum + right.sum;
        //计算最大值
        max = Math.max( max, sum);
        return new Result(true,Math.min(root.val,left.min),Math.max(root.val,right.max),sum);
    }
}

 

333. Largest BST Subtree

Medium

Given the root of a binary tree, find the largest subtree, which is also a Binary Search Tree (BST), where the largest means subtree has the largest number of nodes.

A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties:

• The left subtree values are less than the value of their parent (root) node's value.
• The right subtree values are greater than the value of their parent (root) node's value.

Note: A subtree must include all of its descendants.

Example 1:

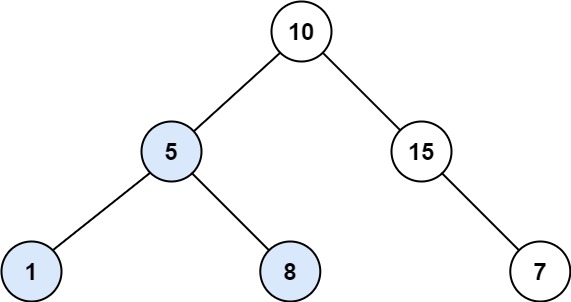
Input: root = [10,5,15,1,8,null,7]
Output: 3
Explanation: The Largest BST Subtree in this case is the highlighted one. The return value is the subtree's size, which is 3.

Example 2:

Input: root = [4,2,7,2,3,5,null,2,null,null,null,null,null,1]
Output: 2 

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -104 <= Node.val <= 104

解法：这个题就是上一题的套娃题

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    class Result{
        int max,min;
        boolean isValid;
        int count;
        Result(boolean isValid,int min,int max,int count){
            this.isValid = isValid;
            this.min = min;
            this.max = max;
            this.count = count;
        }
    }
    private int maxCount = 0;
    public int largestBSTSubtree(TreeNode root) {
        dfs(root);
        return maxCount;
    }
    private Result dfs(TreeNode root){
        if(root==null) return new Result(true,Integer.MAX_VALUE,Integer.MIN_VALUE,0);
        Result left = dfs(root.left);
        Result right = dfs(root.right);
        if(!left.isValid || !right.isValid || root.val<=left.max || root.val>=right.min){
            return new Result(false,0,0,0);
        }
        int currCount = left.count+right.count+1;
        maxCount = Math.max(currCount,maxCount);
        Result curr = new Result(true,Math.min(root.val,left.min),Math.max(root.val,right.max),currCount);
        return curr;
    } 
}