Tree traversal / serialize and deserialize 889, 222, 297,
public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode() {} TreeNode(int val) { this.val = val; } TreeNode(int val, TreeNode left, TreeNode right) { this.val = val; this.left = left; this.right = right; } }
二叉树前序遍历（非递归）
class Solution { public List<Integer> preorderTraversal(TreeNode root) { List<Integer> result = new ArrayList(); if(root==null) return result; Stack<TreeNode> stack = new Stack(); stack.push(root); while(!stack.isEmpty()){ TreeNode temp = stack.pop(); result.add(temp.val);
//因为遍历是先左后右，所以压栈的时候要先右后左 if(temp.right!=null) stack.push(temp.right); if(temp.left!=null) stack.push(temp.left); } return result; } }
二叉树中序遍历（非递归）
class Solution { public List<Integer> inorderTraversal(TreeNode root) { List<Integer> result = new ArrayList(); if(root==null) return result; Stack<TreeNode> stack = new Stack(); while(root!=null || !stack.isEmpty()){ //一直向左走到头，先处理左侧节点 while(root!=null){ stack.push(root); root=root.left; } //输出当前栈顶元素 root = stack.pop(); result.add(root.val); //当前节点压入后，开始处理右侧节点 --这步总出错 root=root.right; } return result; } }
二叉树后序遍历（非递归）
实际上后序遍历，只需要在先序遍历基础上稍作修改即可。
先序遍历：root -> 左 -> 右 先右后左的后序遍历: 右 -> 左 -> root
class Solution { public List<Integer> postorderTraversal(TreeNode root) { List<Integer> result = new ArrayList(); if(root==null) return result; Stack<TreeNode> stack = new Stack(); stack.push(root); while(!stack.isEmpty()){ TreeNode temp = stack.pop(); //此处确保倒序
result.add(0,temp.val); if(temp.left!=null) stack.push(temp.left); if(temp.right!=null) stack.push(temp.right); } return result; } }
垂直遍历
bfs 版本
public class Solution { /** * @param root: the root of tree * @return: the vertical order traversal */ class Node{ TreeNode tn; int pos; Node(TreeNode tn,int pos){ this.tn=tn; this.pos=pos; } } public List<List<Integer>> verticalOrder(TreeNode root) { List<List<Integer>> result = new ArrayList(); if(root==null) return result; Map<Integer,List<Integer>> map = new TreeMap(); Queue<Node> queue = new LinkedList(); queue.offer(new Node(root,0)); while(!queue.isEmpty()){ int size=queue.size(); for(int i=0;i<size;i++){ Node node = queue.poll(); List<Integer> list = map.get(node.pos); if(list==null){ list = new ArrayList(); map.put(node.pos,list); } list.add(node.tn.val); if(node.tn.left !=null) queue.offer(new Node(node.tn.left, node.pos-1)); if(node.tn.right!=null) queue.offer(new Node(node.tn.right,node.pos+1)); } } for(List<Integer> list:map.values()) result.add(list); return result; } }
dfs 版本
public class Solution { /** * @param root: the root of tree * @return: the vertical order traversal */ public List<List<Integer>> verticalOrder(TreeNode root) { Map<Integer,List<int[]>> map = new TreeMap(); dfs(root,0,map,0); List<List<Integer>> result = new ArrayList(); for(List<int[]> list:map.values()){ Collections.sort(list,(x,y)->x[0]-y[0]); List<Integer> temp = new ArrayList(); for(int[] ele:list) temp.add(ele[1]); result.add(temp); } return result; } public void dfs(TreeNode root,int pos,Map<Integer,List<int[]>> map,int level){ if(root==null) return; List<int[]> list = map.get(pos); if(list==null){ list = new LinkedList(); map.put(pos,list); } list.add(new int[]{level,root.val}); dfs(root.left,pos-1,map,level+1); dfs(root.right,pos+1,map,level+1); } }
多节点树的序列化与反序列化
因为不确定子节点的个数，因此我们在节点value之后将子节点的个数记录下来，
因此每个节点都是： label,len,sublabel...
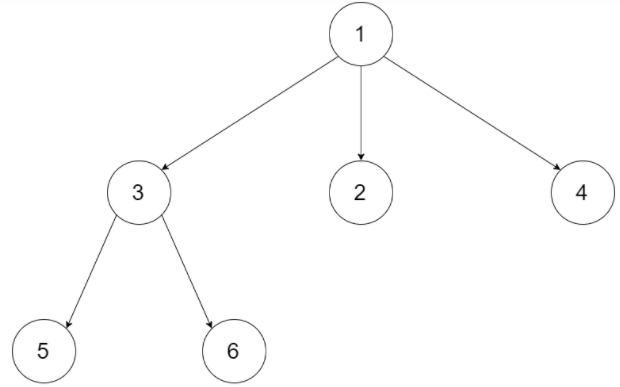
比如上图序列化后： 1,3,3,2,5,0,6,0,2,0,4,0 (红色为长度)
/** * Definition for Directed graph. * class DirectedGraphNode { * int label; * ArrayList<DirectedGraphNode> neighbors; * DirectedGraphNode(int x) { label = x; neighbors = new ArrayList<DirectedGraphNode>(); } * }; */ public class Solution { public String serialize(DirectedGraphNode node) { if(node==null) return ""; String str = "";
str = node.label +","+ node.neighbors.size(); for(DirectedGraphNode temp:node.neighbors){ str = str+","+serialize(temp); } return str; } public DirectedGraphNode deserialize(String data) { if("".equals(data)) return null; Queue<String> queue = new LinkedList(Arrays.asList(data.split(","))); return dfs(queue); } public DirectedGraphNode dfs(Queue<String> queue){ String label = queue.poll(); String len = queue.poll(); DirectedGraphNode dg = new DirectedGraphNode(Integer.parseInt(label)); for(int i=0;i<Integer.parseInt(len);i++){ dg.neighbors.add(dfs(queue)); } return dg; } }
Binary Search Tree 序列化/反序列化
利用binary search tree的特性（左侧节点小于根，右侧节点大于根）
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ public class Codec { // Encodes a tree to a single string. public String serialize(TreeNode root) { if(root==null) return ""; String str = root.val+""; if(root.left!=null) str =str+ "," +serialize(root.left); if(root.right!=null) str =str+ "," +serialize(root.right); return str; } // Decodes your encoded data to tree. public TreeNode deserialize(String data) { if(data.equals("")) return null; Queue<String> queue = new LinkedList(Arrays.asList(data.split(","))); ; return dfs(queue,Integer.MIN_VALUE,Integer.MAX_VALUE); } public TreeNode dfs(Queue<String> queue,int min,int max){ if(queue.isEmpty()) return null; int val = Integer.parseInt(queue.peek()); if(val<=min || val>=max) return null; TreeNode node = new TreeNode(val); queue.poll(); node.left=dfs(queue,min,val); node.right=dfs(queue,val,max); return node; } }
通过preorder和inorder，反序列化二叉树
关键点：
- preorder第一个元素总是二叉树的root
- 通过preorder[start] 可以找到inorder中的位置i
- 通过i的位置将inorder劈成两半，做半片为左子树，右半片为右子树
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public TreeNode buildTree(int[] preorder, int[] inorder) { if(preorder.length==0) return null; return build(preorder,inorder,0,inorder.length-1); } int index = 0; public TreeNode build(int[] preorder, int[] inorder,int start,int end){ TreeNode root = new TreeNode(preorder[index++]); if(start==end) return root; int i = 0; for(i=start;i<=end;i++) if(inorder[i]==root.val) break; if(start<=i-1) root.left = build(preorder,inorder,start,i-1); if(end>=i+1) root.right = build(preorder,inorder,i+1,end); return root; } }
可以通过增加<元素，下标> 的map，来加速获得给元素的下标
class Solution { public TreeNode buildTree(int[] preorder, int[] inorder) { if(preorder.length==0) return null; for(int i=0;i<inorder.length;i++) map.put(inorder[i],i); return build(preorder,inorder,0,inorder.length-1); } private int index = 0; private Map<Integer,Integer> map = new HashMap(); public TreeNode build(int[] preorder, int[] inorder,int start,int end){ TreeNode root = new TreeNode(preorder[index++]); if(start==end) return root; int i = map.get(root.val); if(start<=i-1) root.left = build(preorder,inorder,start,i-1); if(end>=i+1) root.right = build(preorder,inorder,i+1,end); return root; } }
通过preorder和postorder，反序列化二叉树，当然preorder和postorder无法确定唯一的二叉树，因此只要求返回其中一个解
关键点：
- preorder第一个元素是root，第二个元素一定是root的左或右子树的根节点
- 通过第二个元素可以在postorder中的位置即为该子树的最后一个节点
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public TreeNode constructFromPrePost(int[] preorder, int[] postorder) { if(preorder.length==0) return null; return build(preorder,postorder,0,preorder.length-1,0,postorder.length-1); } public TreeNode build( int[] preorder, int[] postorder, int prestart,int preend,int poststart,int postend ){ if(prestart>preend || poststart>postend) return null; TreeNode node = new TreeNode(preorder[prestart]); if(prestart==preend) return node; int pos = 0; for(pos = poststart;pos<postend-1;pos++) if(preorder[prestart+1]==postorder[pos]) break; int leftsize = pos-poststart; node.left = build(preorder,postorder,prestart+1,prestart+1+leftsize,poststart,pos); if(pos+1<postend) node.right = build(preorder,postorder,prestart+2+leftsize,preend,pos+1,postend); return node; } }
889. Convert Binary Search Tree to Sorted Doubly Linked List
解题思路：
1.先把树的遍历写下来
2.在树的遍历基础上，进行指针重新指向
递归方式遍历
/**
* Definition of TreeNode:
* public class TreeNode {
* public int val;
* public TreeNode left, right;
* public TreeNode(int val) {
* this.val = val;
* this.left = this.right = null;
* }
* }
*/
public class Solution {
/**
* @param root: root of a tree
* @return: head node of a doubly linked list
*/
private TreeNode head=null;
private TreeNode tail=null;
public TreeNode treeToDoublyList(TreeNode root) {
if(root==null) return root;
helper(root);
tail.right = head;
head.left = tail;
return head;
}
public void helper(TreeNode root){
if(root==null) return;
helper(root.left);
if(head==null) head = root;
if(tail==null) tail=root;
else {
tail.right = root;
root.left = tail;
tail=root;
}
helper(root.right);
}
}
非递归方式
/** * Definition of TreeNode: * public class TreeNode { * public int val; * public TreeNode left, right; * public TreeNode(int val) { * this.val = val; * this.left = this.right = null; * } * } */ public class Solution { /** * @param root: root of a tree * @return: head node of a doubly linked list */ TreeNode head = null; TreeNode tail = null; public TreeNode treeToDoublyList(TreeNode root) { // Write your code here. if(root==null) return null; Stack<TreeNode> stack = new Stack(); while(root!=null || !stack.isEmpty()){ while(root!=null){ stack.push(root); root=root.left; } root = stack.pop(); if(head==null) head=root; if(tail!=null){ tail.right=root; root.left = tail; } tail=root; root=root.right; } tail.right=head; //坑点，既定记得把首尾节点连接起来!!! head.left=tail; return head; } }
222. Count Complete Tree Nodes
Medium
Given the root of a complete binary tree, return the number of the nodes in the tree.
According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Design an algorithm that runs in less than O(n) time complexity.
Example 1:
Input: root = [1,2,3,4,5,6] Output: 6
Example 2:
Input: root = [] Output: 0
Example 3:
Input: root = [1] Output: 1
Constraints:
- The number of nodes in the tree is in the range
[0, 5 * 104]. 0 <= Node.val <= 5 * 104- The tree is guaranteed to be complete.
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public int countNodes(TreeNode root) { if(root==null) return 0; int leftH = height(root.left);//计算左子树高度 int rightH = height(root.right);//计算右子树高度 //如果左右子树高度相等，那么说明左子树是complete if(leftH == rightH) return (1<<leftH)+countNodes(root.right); //如果左右子树不等，那么说明右子树是complete else return (1<<rightH)+countNodes(root.left); } private int height(TreeNode root){ if(root==null) return 0; return height(root.left)+1; } }
时间复杂度：O(（logN)2 )
297. Serialize and Deserialize Binary Tree
Hard
Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
Example 1:
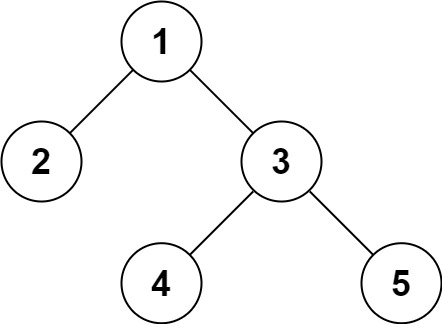
Input: root = [1,2,3,null,null,4,5] Output: [1,2,3,null,null,4,5]
Example 2:
Input: root = [] Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -1000 <= Node.val <= 1000
bfs 层级遍历进行serialize/deserialize
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ public class Codec { // Encodes a tree to a single string. public String serialize(TreeNode root) { StringBuffer sb = new StringBuffer(); Queue<TreeNode> queue = new LinkedList(); queue.offer(root); while(!queue.isEmpty()) { TreeNode curr = queue.poll(); if(curr == null){ sb.append("#"); } else{ sb.append(curr.val); queue.offer(curr.left); queue.offer(curr.right); } if(!queue.isEmpty()) sb.append(","); } return sb.toString(); } // Decodes your encoded data to tree. public TreeNode deserialize(String data) { String[] arr = data.split(","); TreeNode[] tarr = new TreeNode[arr.length]; for(int i = 0; i < arr.length; i++) { if(arr[i].equals("#")) tarr[i] = null; else tarr[i] = new TreeNode(Integer.parseInt(arr[i])); } int slow = 0, fast = 1; TreeNode root = tarr[0]; //slow：每次向右移动一个位置 //fast：如果root为null 不移动，如果root不为null 移动两个位置 while(fast < tarr.length) { TreeNode node = tarr[slow]; if(node != null) { node.left = tarr[fast]; node.right = tarr[fast + 1]; fast += 2; } slow++; } return root; } } // Your Codec object will be instantiated and called as such: // Codec ser = new Codec(); // Codec deser = new Codec(); // TreeNode ans = deser.deserialize(ser.serialize(root));
dfs preorder 遍历进行serialize/deserialize
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ public class Codec { // Encodes a tree to a single string. public String serialize(TreeNode root) { if(root == null) return "#"; return root.val + "," + serialize(root.left) + "," + serialize(root.right); } // Decodes your encoded data to tree. public TreeNode deserialize(String data) { Queue<String> queue = new LinkedList(Arrays.asList(data.split(","))); return helper(queue); } private TreeNode helper(Queue<String> queue) { String curr = queue.poll(); if(curr.equals("#")){ return null; } TreeNode root = new TreeNode(Integer.parseInt(curr)); root.left = helper(queue); root.right = helper(queue); return root; } } // Your Codec object will be instantiated and called as such: // Codec ser = new Codec(); // Codec deser = new Codec(); // TreeNode ans = deser.deserialize(ser.serialize(root));
Medium
You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.
In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.
Return the minimum number of moves required to make every node have exactly one coin.
Example 1:
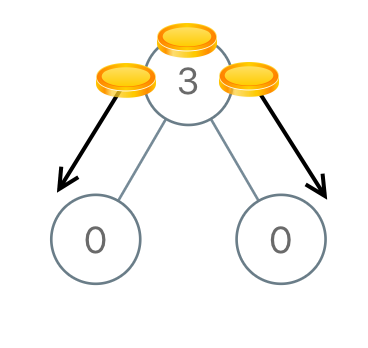
Input: root = [3,0,0] Output: 2 Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.
Example 2:
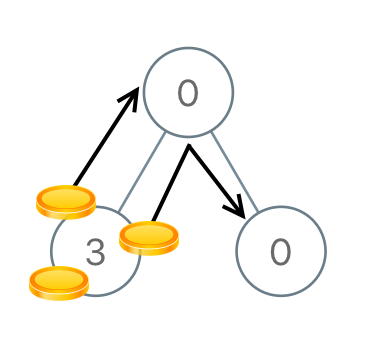
Input: root = [0,3,0] Output: 3 Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.
Constraints:
- The number of nodes in the tree is
n. 1 <= n <= 1000 <= Node.val <= n- The sum of all
Node.valisn.
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { /** 关键点： 1. 后续遍历（先算子树，再算根） 2. 从每个子树的角度计算是需要移入还是移出coin */ int total = 0; public int distributeCoins(TreeNode root) { helper(root); return total; } private int helper(TreeNode root) { if(root == null) return 0; // 计算左子树的自身平衡性，如果coin多于本身节点数(返回为正)，需要移出coin；否则返回为负，需要移入coin int left = helper(root.left); //无论正负都需要计入移动步数 total += Math.abs(left); // 计算右子树的自身平衡性，如果coin多于本身节点数(返回为正)，需要移出coin；否则返回为负，需要移入coin int right = helper(root.right); total += Math.abs(right); // 对于root节点，左子树平衡性+右子树平衡性 + root 本身value - 1，即为当前子树整体平衡性 return left + right + root.val - 1; } }
浙公网安备 33010602011771号