『学习笔记』倍增
概念
在进行递推时,如果一个一个递推,时间复杂度是线性的,在 \(n\) 巨大的时候就会严重超时。于是我们采用成倍增长的方式进行递推,把所有 \(f_{2^i}\) 求出来。当我们想要某个位置的值时,我们利用十进制与二进制的每个数一一对应的性质即每个数都能拆成多个 \(2\) 的整数次幂的和(二进制拆分),使用原本已求出来的值来求我们想求出的值。
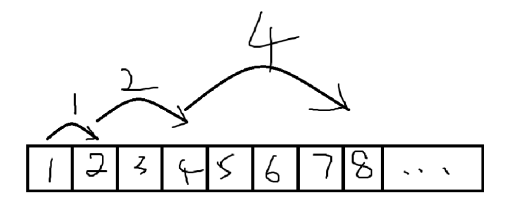
倍增的几大用处有 ST 表,LCA 和(矩阵)快速幂。
ST 表
引入
ST 表处理的是所有符合结合律且可重复贡献的信息查询(包括但不限于 RMQ、最大公因数、最小公倍数、按位与、按位或)。它是基于倍增和动态规划的思想,可以实现离线 \(\mathcal{O}(n\log_2n)\) 预处理、在线 \(O(1)\) 查询,但是不支持在线修改。
例题
方法一:暴力查找
对于每次询问,查找 \(\max\limits_{i\in[l,r]}\{a_i\}\),最直接的做法就是每次询问都遍历一遍查询最大值。
时间复杂度 \(\mathcal{O}(n\times m)\),空间复杂度 \(\mathcal{O}(n)\)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n, m, a[N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
while(m--) {
int l, r, maxi = -1;
cin >> l >> r;
for(int i = l; i <= r; i++) {
maxi = max(maxi, a[i]);
}
cout << maxi << '\n';
}
return 0;
}
方法二:暴力预处理
不难想到由于会有重复的区间,所以可以预处理出所有 \([l,r]\) 的最大值,询问时直接输出即可。
此做法适用于 \(n\) 不大,但 \(m\) 很大,时间复杂度 \(\mathcal{O}(n^2)\),空间复杂度 \(\mathcal{O}(n^2)\)
for(int i = 1; i <= n; i++) {
f[i][i]= a[i];
for(int j = i + 1; j <= n; j++) {
f[i][j] = max(f[i][j - 1], a[i]);
}
}
方法三:ST 表预处理
我们令 \(f_{i,j}\) 表示从 \(i\) 开始的 \(2^j\) 个元素的最大值,需要满足 \(1\le i\le n\) 且 \(i+2^j-1\le n\)。
显然 \(f_{i,0}=a_i\)。我们从 \(i-1\) 转移到 \(i\),在 \([i,i+2^j-1]\) 内长度为 \(2^{j-1}\) 的子区间有两个,分别是 \([i,i+2^{j-1}-1]\) 和 \([i+2^{j-1},i+2^j-1]\),两个子区间的最大值是 \(f_{i,j-1}\) 和 \(f_{i+2^{j-1},j-1}\)。
从而得到状态转移方程为:
预处理完后我们来思考一下对于任意区间 \([l,r]\) 的最大值该分成哪几个子区间。
令 \(k=\log_2\{len_{[l,r]}\}=\log_2\{r-l+1\}\),则第一个想到的子区间必然是 \([l,l+2^k-1]\),然而剩下的子区间 \([l+2^k,r]\) 的长度不一定为 \(2\) 的整数次幂,这就体现了区间最大的可重复贡献的性质,这也就代表两个子区间可以有交集,所以另一个区间是 \([r-2^k+1,r]\)。
由于 \(\log\) 函数常数较大,所以可以递推预处理出 \(1\sim n\) 的 \(\log\) 值,\(h_i=h_{\left\lfloor i\div 2\right\rfloor}+1\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int n, m, a[N], f[N][25], h[N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> a[i];
f[i][0] = a[i];
}
for(int i = 1; i <= 20; i++) {
for(int j = 1; j + (1 << i) - 1 <= n; j++) {
f[j][i] = max(f[j][i - 1], f[j + (1 << (i - 1))][i - 1]);
}
}
for(int i = 2; i <= n; i++) {
h[i] = h[i / 2] + 1;
}
while(m--) {
int l, r, s, ans;
cin >> l >> r;
s = h[r - l + 1];
ans = max(f[l][s], f[r - (1 << s) + 1][s]);
cout << ans << '\n';
}
return 0;
}
练习
-
luogu P3865 【模板】ST 表:区间最大
-
luogu P1816 忠诚:区间最小
-
luogu P2251 质量检测:区间最小
LCA 最近公共祖先
引入
在一棵有根树上的两个节点 \(u,v\),它两的祖先集合 \(f(u)\) 和 \(f(v)\) 的交集 \(f(u)\cap f(v)\) 里深度最大的节点元素。
例题
方法一:暴力查找
我们先把 \(u\) 的所有祖先标记出来,接着让 \(v\) 向上推进,如果第一次找到一个被标记的节点 \(w\),则其一定是 \(u,v\) 的最近公共祖先。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int n, m, s, f[N], ans;
bool vis[N];
vector<int> e[N];
inline void dfs(int x, int fa) {
f[x] = fa;
for(int i : e[x]) {
if(i == fa) {
continue;
}
dfs(i, x);
}
}
inline void dfs1(int x) {
vis[x] = 1;
if(x == s) {
return ;
}
dfs1(f[x]);
}
inline void dfs2(int x) {
if(ans) {
return ;
}
if(vis[x]) {
ans = x;
return ;
}
dfs2(f[x]);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> s;
for(int i = 1; i < n; i++) {
int x, y;
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
dfs(s, 0);
while(m--) {
ans = 0;
int a, b;
cin >> a >> b;
memset(vis, 0, sizeof(vis));
dfs1(a);
dfs2(b);
cout << ans << '\n';
}
return 0;
}
方法二:倍增求 LCA
先 dfs 预处理出每个节点的深度和 \(2^k\) 的祖先。
代码如下:
int f[N][21], dep[N];
inline void dfs(int u, int fa) {
dep[u] = dep[fa] + 1;
f[u][0] = fa;
for(int i = 1; i <= 20; i++) {
f[u][i] = f[f[u][i - 1]][i - 1];
}
for(int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
if(v == fa) {
continue;
}
dfs(v, u);
}
}
然后对于两个节点 \(u,v\),不妨设 dep[u] >= dep[v]。枚举 \(i\) 从 \(20\) 至 \(0\),每次只要 dep[fa[u][i]] >= dep[v],那么就 u = fa[u][i]。这个过程类似于二进制拆分。
等 \(u,v\) 的深度相同时,再让 \(u,v\) 同时往上推进,直到相等。
代码如下:
inline int lca(int x, int y) {
if(dep[x] < dep[y]) {
swap(x, y);
}
for(int i = 20; i >= 0; i--) {
while(dep[f[x][i]] >= dep[y]) {
x = f[x][i];
}
if(x == y) {
return x;
}
}
for(int i = 20; i >= 0; i--) {
if(f[x][i] != f[y][i]) {
x = f[x][i], y = f[y][i];
}
}
return f[x][0];
}
练习
-
luogu P2420 让我们异或吧(注:此题由于按位异或具有任何数和自己异或结果为零的性质,所以可以不用 LCA)
快速幂
引入
由于直接求 \(a^b\bmod p\) 时间复杂度为 \(\mathcal{O}(b)\),所以可以采用 \(a^b=(a^{\left\lfloor b\div 2\right\rfloor})^2\times\begin{cases}a&\text{if }b\equiv1\pmod 2\\1&\text{if }b\equiv0\pmod2\end{cases}\) 来进行递推或递推。
例题
方法一:递归
显然,\(a^0=1\),所以递归边界为 \(b=0\)。令 tmp = qpow(b / 2) 转移就是 qpow(b) = t * t % p * (b & 1 ? a : 1) % p。
代码如下:
inline int qpow(int a, int n) {
if(!n) {
return 1;
}
int tmp = qpow(a, n / 2);
if(n & 1) {
return tmp * tmp % p * a % p;
} else {
return tmp * tmp % p;
}
}
方法二:递推
思路同上,代码如下:
inline int qpow(int a, int n) {
int ans = 1;
while(n) {
if(n & 1) {
ans = (ans * a) % p;
}
a = (a * a) % p;
n >>= 1;
}
return ans % p;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号