2025.7暑假培训笔记
数据结构部分及动态规划部分的讲课代码:https://wwdw.lanzouo.com/iGv0D315z43c
数据结构

课件(讲义):https://wwdw.lanzouo.com/igO2P3144atc 密码fszt
OI-wiki:https://oi-wiki.org/ds/
ST表
概述
ST表的作用:在𝑂(𝑛 𝑙𝑜𝑔 𝑛)的时间内预处理完后,可在𝑂(1)的时间查询区间最值。
𝑓[𝑖][𝐿]表示以L为开头,长度为2^𝑖的区间的最大(小)值,即对应于[𝐿,𝐿+2^𝑖−1]。
通过𝑓[𝑖][…]可以推出𝑓[𝑖+1][…] 𝑓[𝑖+1][𝐿]=max(𝑓[𝑖][𝐿],𝑓[𝑖][𝐿+2^𝑖])。
考到的概率不高,除了树状数组或者线段树、区间最值(大量处理);太吃空间了,当板子写即可。
预处理:O(n log n)
查询:O(1)
操作(查询)
对于[3,9],等同于max([3,3+2^2−1],[6,6+2^2−1])
所以,每次查询时,我们寻找两段合并起来刚好是当前区间的预处理过的区间,对他们求最值即可。
例题
https://www.luogu.com.cn/problem/P3865
https://www.luogu.com.cn/problem/P1198
RMQ&LCA问题
用到的前置知识
树:
N个点,N-1条边的连通图。或者说,没有环的连通图;
一个节点的深度定义为到根节点的距离。
如何存储一棵树?
使用Vector[i]存储与节点i相邻的点的编号(稀疏图的存储方式)
如何遍历一棵树?
从树根开始,DFS递归遍历,每次遍历记录父亲是谁,避免死循环。
概述
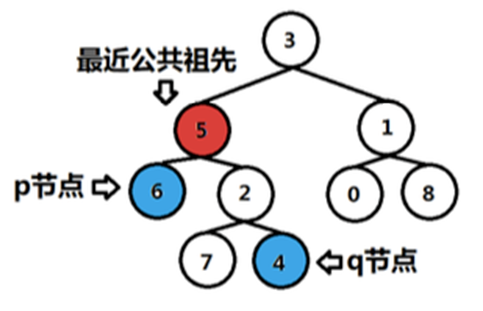
LCA(最近公共祖先)问题:
有一颗N个节点的树,有M次询问,每次询问给出两个点u,v,求u,v在树上的最近公共祖先(即深度最深的公共祖先)。
节点A是节点B的祖先当且仅当A在B到根的路径上。
反之,如果B在A的子树里,则B是A的后代。
解法1
通过欧拉遍历序(ETT)转化为区间最值(RMQ)问题。
生成一棵树的欧拉遍历序:
从根节点开始遍历,每次到达或者返回一个节点,
将这个节点的编号放入序列末尾。
对于下图则是:
1 2 3 2 5 6 5 2 1 4 1
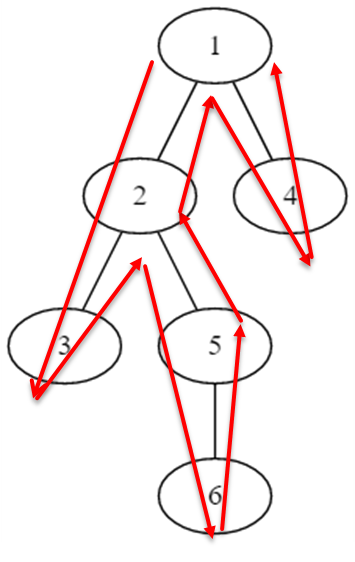
先遍历一遍树,生成欧拉遍历序。
我们记录给每个点它在欧拉遍历序中的任意一个出现位置p[u]。
那么查询u,v的最近公共祖先,即为查询区间[p[u],p[v]]中深度最潜的一个点是什么。
关于上图的解释:
欧拉遍历序: 1 2 3 2 5 6 5 2 1 4 1
对应点深度: 0 1 2 1 2 3 2 1 0 1 0
数组下标: 1 2 3 4 5 6 7 8 9 10 11
比如查询(5,4),则对应区间[5,10]或者[7,10],
区间中深度最小值为0,对应了节点1。
解法2
树上倍增法 (ST表建在树上):
预处理:
𝑓[𝑖][𝑗]表示从节点j往上走2^𝑖步会到哪里,例如𝑓[𝑖][0]记录i的父亲。
由于向上走2^𝑖步,等于走2^(𝑖−1)步,再走2^(𝑖−1)步,
所以𝑓[𝑖][𝑗]=𝑓[𝑖−1][𝑓[𝑖−1][𝑗]];
预处理时同时记录每个节点的深度𝑑[𝑖]。
查询时先通过倍增法使得深度更深的点,向上走到与另一个点相同的深度,然后再次运用倍增法走到两个点深度最浅的不同的祖先。
例子:
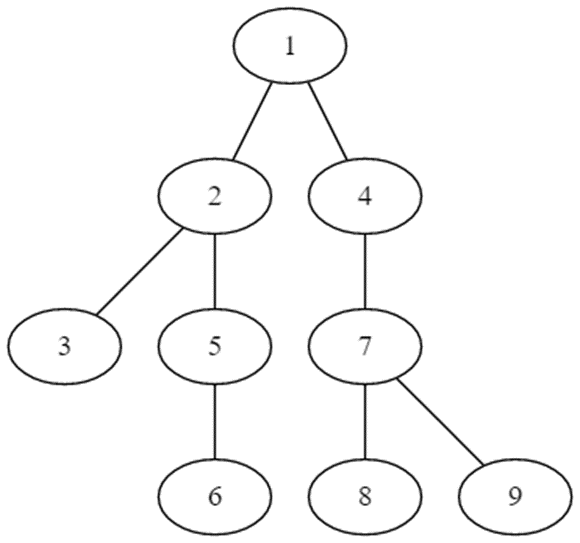
比如在上图中查询(5,9)的最近公共祖先
首先从9向上走到与5同一深度的7
然后5和7分别走到2和4
于是(5,9)的最近公共祖先就是2或者4的父亲(1)。
例题
https://www.luogu.com.cn/problem/P3379
https://www.luogu.com.cn/problem/P2420
并查集
概述
并查集实际维护的内容,可以看做是对集合的维护,且支持合并集合。
并查集的维护思路是,将每个集合做成一颗树型,用树的根作为集合的标志。
那么,判断两点是否在一个集合内,只要找到两点所在树的树根,判断是否相同即可。
合并两个集合时,让一颗树的树根父亲设为另一颗树的树根即可。
用这样的结构即可维护点与点间连通性判定,但是,显然最坏这样复杂度会达到𝑂(𝑛^2)。
优化:按秩合并
显然复杂度是和树高相关的,因此可以考虑如何减少树高。
设rank表示树的树高,又称秩。当合并两颗秩相同的树时,就会将秩加一。若秩不同,我们一定将秩小的树的根的父亲设为秩大的树的根。这样显然能尽量减少树高。
容易归纳证明,按这样方法出现一棵秩为𝑥的树,这棵树至少有2^𝑥−1个点。
因此rank<=log n,可以证明该优化将复杂度降到了𝑂(𝑛 log(𝑛))。
优化:路径压缩
思路:树内部结构实际上不重要。因此每当我们查找了一个点,我们一定会遍历该点到树根的所有点,不妨直接将这些点的父亲改为树根。
那么路径压缩复杂度:
它的上界用势能分析可以证明是𝑂(𝑛 log𝑛的,这里略去。
那么下界如何?很可惜,也是𝑂(𝑛 log 𝑛)的。
我们尝试构造数据把并查集卡到log n。
定义树 B(i),B(0) 只有一个点,B(i) = merge B(i-1) , B(i-1)。
先用若干操作构造B(log n)。
不断执行以下操作
加入一个点,把根连过去
FIND 最深的那个点
如下图所示:
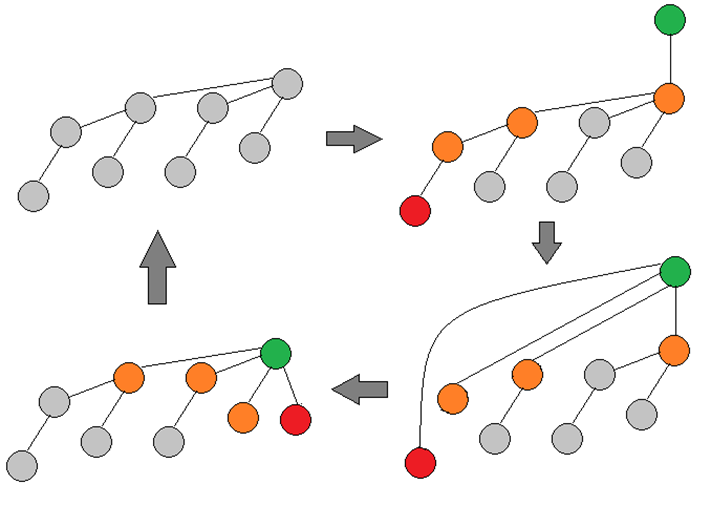
优化:并查集
实际上,大多数出题人不卡路径压缩,路径压缩已经足够用了(大多数题目的数据里,路径压缩有犹如𝑂(𝑛)的效率)。
并查集可以有更低的复杂度吗?答案是肯定的。
如果我们同时使用路径压缩和按秩合并,可以用势能分析证明此时并查集的复杂度为𝑂(𝑛 𝛼(𝑛)),其中𝛼(𝑛)为反阿克曼函数,可以认为其不超过5。
典例剖析
初始有
n个点,它们之间没有边,现在有m次操作。
共有两种操作,添加一条边 或者 询问两点在哪次操作后联通。
强制在线。约束范围:
n,m<=100000
我们可以使用并查集的按秩合并(但是不要路径压缩)。
两个集合被合并起来,连上的边的权值就设为当前时间。
然后我们可以发现,询问j与k何时联通,就是查询j与k树路径上边权最大值。因为我们按秩合并了,所以树高是log n的,并不会超时。
拓展
对于一个图G=(V,E),如果能够将点集分成V1和V2,满足V1内无边,V2内也无边,那么可称G是二分图。
即,如果能够对每个点进行黑白染色,使得不存在一条边连接两个同色点,则该图是二分图。
上面两个易证互为充要。
如何判断一个图是否为二分图?
答:并查集染色。
容易证明,一个图是二分图当且仅当其不存在奇环。
考虑下列算法:
初始所有点在一个集合内。每个点维护一个颜色(0或1),初始全为0。该颜色表示如果其父亲颜色为0,该点应该为什么色。
显然对于一个连通二分图,一旦确定一个点的颜色,其余点颜色也固定。
依次加入图的每一条边。如果该边连接的两点在同一集合内,检查它们颜色是否相同。
否则合并集合,通过讨论情况可能会更改被合并树树根的颜色。
例题
https://www.luogu.com.cn/problem/P3367
线段树
传统线段树(原理)
对于单点修改:维护区间信息。
要求区间信息能够快速合并。
单次操作复杂度为O(信息合并复杂度)*log(N)
所以区间信息合并一般常见速度为O(1)或者O(logN)之类低复杂度,或均摊低复杂度。
对于区间修改:
区间信息能够合并;
区间标记能够合并;
区间标记能够快速修改区间信息。
典例剖析
小白逛公园 https://www.luogu.com.cn/problem/P4513
在小新家附近有一条“公园路”,路的一边从南到北依次排着n个公园,小 白早就看花了眼,自己也不清楚该去哪些公园玩了。
一开始,小白就根据公园的风景给每个公园打了分-.-。小新为了省事,每次遛狗的时候都会事先规定一个范围,小白只可 以选择第a个和第b个公园之间(包括a、b两个公园)选择连续的一些公园玩。小白当然希望选出的公园的分数总和尽量高 咯。同时,由于一些公园的景观会有所改变,所以,小白的打分也可能会有一些变化。 那么,就请你来帮小白选择公园吧。
11≤N≤500 0001 个公园,11≤M≤100 0001 次修改。
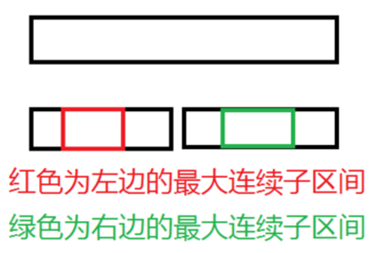
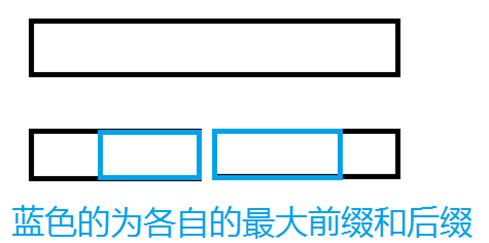
对于每个区间,维护一个左边的最大前缀,右边的最大后缀,以及区间内部的答案;
每次合并的时候,即答案选取左子区间的max,右子区间的max,或者左子区间的最大后缀,右子区间的最大前缀即可。
如图:
拓展
常见的打标记操作:
- 区间加
- 区间乘
- 区间染色(区间修改为一个数)
- 区间翻转(需要更高级的数据结构,如 Treap LCT)
- 区间xor
例题
https://www.luogu.com.cn/problem/P1471
https://www.luogu.com.cn/problem/P6327
https://www.luogu.com.cn/problem/P3215
https://www.luogu.com.cn/problem/P4036
线段树+有限暴力(典例)
楼房重建 https://www.luogu.com.cn/problem/P4198
有一排楼,每次把一个位置的楼的高度修改为
x,每次输出可以从最左边看到的楼个数。形式化来说,给一个序列
a,每次修改一个位置的值,查询有多少个位置i满足[1,i-1]里的所有j,都有𝑎[𝑗]<𝑎[𝑖]。
一个楼房能被看到可以等价于它的斜率比之前的任何一个都大;
所以说我们这里可以直接维护斜率,而不用管楼的高度。
问题转化为:
- 单点修改
- 查询全局有多少位置是前缀最大值
使用分块维护即可。
或者使用另一种解法,线段树:
考虑用线段树维护。
对于线段树每个结点维护两个值:ans和max,ans表示只考虑这个区间内的可以被看到的楼房,max表示这个区间的最大楼房斜率。
合并左右区间的时候:显然左区间的答案不会变化。
问题就是考虑右区间有多少个楼房在左区间的约束条件下仍然可以被看到
如果右区间最大值都小于等于左区间最大值,那么右区间就没有贡献了,相当于是被整个挡住了。
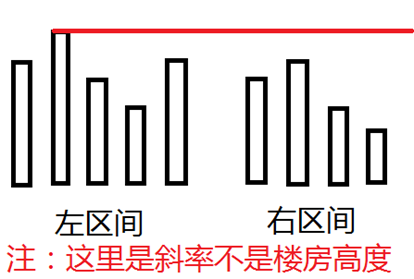
如果右区间最大值大于左区间最大值;
考虑右区间的两个子区间:左子区间、右子区间。
如果左子区间的最大值小于等于左区间最大值,那么就递归处理右子区间。
因为相当于左子区间里面所有楼房都被前面的楼房挡住了了,递归查询右边有多少楼房没被挡住。
否则就递归处理左子区间,然后加上右子区间原本的答案,因为这个约束条件弱于左子区间对右子区间的约束,所以只考虑这个约束条件对左子区间的影响。
拓展
线段树合并:
- 复杂度
O(nlogn); - 可以合并带标记的线段树;
- 同时还能维护信息。
树链剖分
概述
- 可以将树上的问题转化为序列上的问题;
- 可以将一条链拆分成
O(logN)个连续的DFS序区间; - 可以将一颗子树对应一个区间;
- 同时对于换根操作也可以支持。
树链剖分+DFS序:
- 树链剖分把树上的链问题,转换成了序列上的区间问题;
- DFS序把树上的子树问题,转换成了序列上的区间问题;
- 常见的DFS序有两种,长度为
N和长度为2N的。
典例1
软件包管理器(来源未知)
一颗N个点的树,每个点上有权值,一共会有Q个操作。
分为四种:
- 把U到V路径上所有点的点权+X
- 求U到V路径上所有点的点权和Mod 1e9+7
- 把U的子树的所有点的点权+X
- 求U的子树的点权和Mod 1e9+7
约束范围:
N,Q≤1e5
综合运用上述DFS序及树链剖分即可。
典题2
遥远的国度 https://www.luogu.com.cn/problem/P3979
原题略。
换根,链修改,子树询问。
典例剖析
网络管理(来源未知)
给出一颗n个结点的树,点上有权值;
两种操作:
1.修改某个结点的权值;
2.求x,y路径上第K大值。约束范围:
N,Q<=80000
大力数据结构? O(nlog4n)
修改可以表示为加上或者减去一条权值线段树链;
修改O(nlog2n);
采用带有+1和-1的DFS序,一个点到根的路径就是DFS序的前缀和。
查询O(nlog2n)。
例题
https://www.luogu.com.cn/problem/P3384
https://www.luogu.com.cn/problem/P2590
https://www.luogu.com.cn/problem/P4211
https://www.luogu.com.cn/problem/P4679
简单分块
概述
对于分块操作:

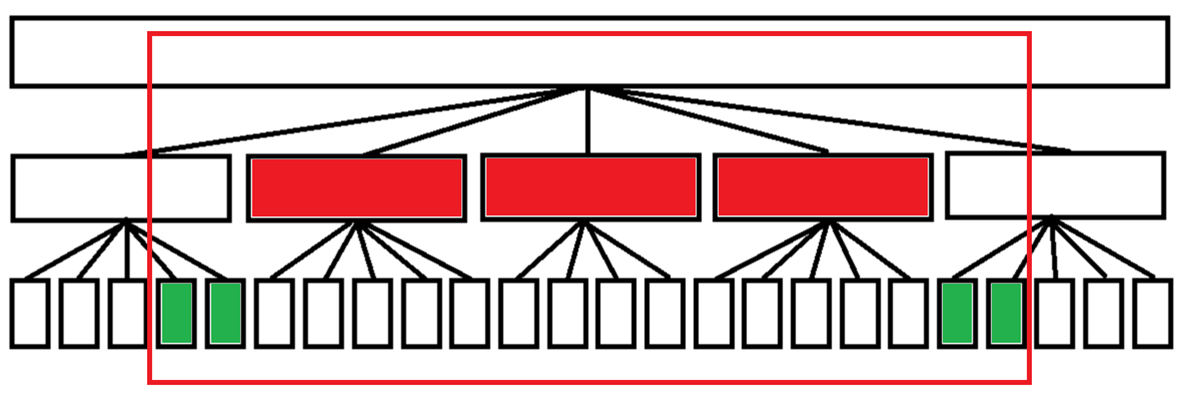
- 我们把每次操作完整覆盖的块定义为“整块”(红);
- 把每次操作没有完整覆盖的块定义为“零散块”(绿)。
每次操作最多经过O(sqrt(n))个整块,以及2个零散块;
所以我们可以O(1)维护整块信息,O(sqrt(n))查询零散块信息;
这样就达到了O(msqrt(n))的复杂度。
上述“整块”和“零散块”另一种形式:
运用例
维护一个序列实现:
1.区间加
2.查询区间小于x的数个数
分块,维护每块的OV(就是排序后的数组);
每次区间加的时候:整块可以打一个标记,零散块可以重构。
每次查询的时候:
整块查询小于x的数,这个整块的标记为y(也就是说这一块所有数都加了y);则等价于查整块的排序后的数组里面小于x-y的数的个数,这个可以二分。
零散块就直接暴力查询块内在查询区间内的数是否满足条件。
典例剖析
由乃打扑克 https://www.luogu.com.cn/problem/P5356
原题略。
将块大小设为sqrt(n)log n,每次修改显然复杂度为sqrt(n)logn
二分答案,每次查询:
- 有
sqrt(n)/logn个整块,这部分复杂度为O(sqrt(n))单次; - 有sqrt(n)logn个零散的点,这部分复杂度为
O(sqrt(n)log n)单次。
想办法优化掉零散点的复杂度:可以预先先把零散的两个块归并成为一个假的块,这样我们每次二分答案之后只用在这个假的块上面二分即可。
总复杂度O(m sqrt(n) log n)
例题
https://www.luogu.com.cn/problem/P3396
https://www.luogu.com.cn/problem/P1972
https://www.luogu.com.cn/problem/P2801
动态规划

课件(讲义):https://wwdw.lanzouo.com/idbAl3145jcf 密码:5obb
OI-wiki:https://oi-wiki.org/dp/
背包DP
概述
背包问题是DP中一类非常经典的问题。
除了普通的背包问题,还有多重背包等变种问题,见下述。
背包问题著名参考资料,背包九讲
https://www.kancloud.cn/kancloud/pack/70125
01背包
典例剖析
有
N件物品和一个容量为V的背包。第i件物品的体积是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。每个物品只能取一次或者不取。约束范围:
1≤𝑁,𝑉≤1000
贪心思路很明显,考虑靠近DP的方式。
f[i][v]表示前i件物品体积和为v可以获得的最大价值和。
易得𝑓[𝑖][𝑣]=max{𝑓[𝑖−1][𝑣],𝑓[𝑖−1][𝑣−𝑐[𝑖]]+𝑤[𝑖]}
尝试优化掉第一维的空间复杂度,重复使用数组:
for i=1..N
for v=V..0
f[v]=max{f[v],f[v-c[i]]+w[i]};
完全背包
典例剖析
有
N种物品和一个容量为V的背包,每种物品数量不限。第i种物品的体积是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。约束范围:
1≤𝑁,𝑉≤1000
令f[i][v]表示前i种物品体积和为v的最大价值和。
易得:𝑓[𝑖][𝑣]=max{𝑓[𝑖−1][𝑣−𝑘∗𝑐[𝑖]]+𝑘∗𝑤[𝑖]│0<=𝑘∗𝑐[𝑖]<=𝑣}
简单优化:𝑓[𝑖][𝑣]=max【{𝑓[𝑖−1][𝑣],𝑓[𝑖][𝑣−𝑐[𝑖]]+𝑤[𝑖]}】
优化空间后:
for i=1..N
for v=0..V
f[v]=max{f[v],f[v-cost]+weight}
多重背包
典例剖析
有
N种物品和一个容量为V的背包。第i种物品的体积是c[i],价值是w[i],一共有n[i]个。求解将哪些物品装入背包可使价值总和最大。约束范围:
1≤𝑁,𝑉≤1000
令f[i][v]表示前i种物品体积和为v的最大价值和。
易得:𝑓[𝑖][𝑣]=max{𝑓[𝑖−1][𝑣−𝑘∗𝑐[𝑖]]+𝑘∗𝑤[𝑖]│0<=𝑘≤𝑛[𝑖]}
复杂度O(V∗Σn[i])
二进制分组优化,如果n[i]为13,就将这种物品分成系数分别为1,2,4,6的四件物品。这样转化为01背包问题。
复杂度 O(V 𝑁 𝑙𝑜𝑔 N)
例题
https://www.luogu.com.cn/problem/P1616
https://www.luogu.com.cn/problem/P1048
https://www.luogu.com.cn/problem/P1776
https://www.luogu.com.cn/problem/P1782
序列、数位DP
概述
这类问题一般按照序列从左往右顺序DP,常见优化有数据结构优化区间最值、区间和、前缀和优化或者单调队列。
常见的序列DP类型有:字符串上的DP、数列上的DP、数位上的DP。
典例剖析1
小俊很喜欢数学,现在他要给你出一道严肃的数学题。定义
F[x]为x在十进制表示下各位数字的异或和,例如F(1234) = 1 xor 2 xor 3 xor 4 = 4。给你两个数a,b(a≤b)。求F[a] + F[a+1] + F[a+2]+…+ F[b−2] + F[b−1] + F[b]模109+7的值 。保证a,b的长度不超过100000。
一个非常显然的数位DP。
依旧拆成1~b和1~a-1两部分计算。
从头到尾依次DP, dp[i][j]表示i位数中异或和为j的数的个数。然后开始枚举当前数字哪一位与上限不同,然后进行统计。
复杂度O(|a|*10*16)
典例剖析2
给出一个序列
A,求A最长的子序列B,满足𝐵[𝑖] 𝑎𝑛𝑑 𝐵[𝑖−1]≠0。约束范围:
1≤序列长度≤10^5,1≤数值范围≤10^9
dp[i][j]表示原来序列前面i个数,选取的子序列的最后一个数的第j位是1的时候,子序列最长的长度。
然后转移非常显然。
拓展
环形DP的处理方式:
通常通过将环复制两遍的方式来转化为序列DP;
或者通过枚举环上一个位置断开,从而转化为序列DP。
典例剖析3
石子合并 https://www.luogu.com.cn/problem/P1880
原题略。
从头开始把环复制一遍,变成一个长度为2N的序列。
然后DP[i][j]表示合并区间[i,j]的所有石子的最大得分,枚举区间分界点,O(N^3)。
例题
https://www.luogu.com.cn/problem/P1616
https://www.luogu.com.cn/problem/P1858
https://www.luogu.com.cn/problem/P1489
https://www.luogu.com.cn/problem/P1091
区间DP
概述
区间DP一般解决一些区间上的问题,往往和序列DP较难区分,如果一道题序列DP无法处理,可以考虑区间DP。
通常dp[i][j]表示区间[𝑖,𝑗]的最优值是多少,然后根据枚举分界点来转移。
典例剖析1
折叠的定义如下:
一个字符串可以看成它自身的折叠。记作
S -> S
X(S)是X(X>1)个S连接在一起的串的折叠。记作X(S) -> SSSS…S(X个S)。如果
A -> A’,B->B’,则AB -> A’B’例如,因为3(A) = AAA,2(B) = BB,所以3(A)C2(B)->AAACBB,而2(3(A)C)2(B)->AAACAAACBB给你一个字符串(长度保证不超过100),求它的最短折叠。
例如
AAAAAAAAAABABABCCD的最短折叠为:9(A)3(AB)CCD
又例如NEERCYESYESYESNEERCYESYESYES的最短折叠为2(NEERC3(YES))
DP[i][j]表示区间[𝑖,𝑗]的最小表示。
然后根据三种构造方法,对应了三种转移:
1、S->S ,非常显然
2、X(S) ,枚举X,检查是否可以表示成X(S)
3、AB ,枚举分界点
复杂度𝑂(𝑁^3)(2用KMP)或𝑂(𝑁^4)
典例剖析2
假设你有一条长度为5的木版,初始时没有涂过任何颜色。你希望把它的5个单位长度分别涂上红、绿、蓝、绿、红色,用一个长度为5的字符串表示这个目标:
RGBGR。每次你可以把一段连续的木版涂成一个给定的颜色,后涂的颜色覆盖先涂的颜色。例如第一次把木版涂成
RRRRR,第二次涂成RGGGR,第三次涂成RGBGR,达到目标。给出一个字符串(长度不超过300),用尽量少的涂色次数达到目标。
输出最少的涂色次数。
因为是区间涂色,如果s[l]=s[r],那么我们显然可以用一次覆盖[l,r],然后中间的再另外考虑。
f[l][r]表示使[l,r]成为规定颜色的最小次数。
f[l][r]=min(f[l][k]+f[k+1][r])f[l][r]=min(f[l+1][r],f[l][r-1])左右端点颜色一样
典例剖析3

题意不难理解,按照要求一步步往下思考:
DP[i][j][0/1/2]表示区间[𝑖,𝑗]最后一个人一定是最左边的/最右边的/两边都可以的方案数。
如此DP即可。
例题
https://www.luogu.com.cn/problem/P1063
https://www.luogu.com.cn/problem/P1622
树形DP
概述
树上DP一般分为两类,一类是O(N)的树上递推;一类是以子树为单位的转移即DP[i]表示子树i的最优解。
典例剖析1

树上递推。
令𝑎𝑛𝑠_𝑖为在第i个点举行聚会,司机需要的最少时间,𝑠𝑢𝑚为所有人家的生成树的所有边权之和,𝑑𝑖𝑠_𝑖为点i到生成树的最短距离,𝑚𝑎𝑥𝑙𝑒𝑛_𝑖为所有人家的生成树加上点i所构成的生成树中从点i出发的最长边;
得𝑎𝑛𝑠_𝑖=2⋅(𝑠𝑢𝑚+𝑑𝑖𝑠_𝑖)−𝑚𝑎𝑥𝑙𝑒𝑛_𝑖
进行4次dfs即可求出。
典例剖析2

带权二分,注意这类的正确性不容易证明。
直接DP会爆炸,随着 K 的增加,答案是先增大再减小。
二分选一条路径额外带来的收益(可为负),然后不限制路径条数地 DP ,只是附带着记录一下选了几条路。最后看选出来的路径如果多于 K+1 条,说明选一条路径的收益太高;不然说明收益太低。当不看路径条数地 DP 的最优解恰好选了 K+1 条路径时就可以退出了。答案就是现在这个最优解减去 “路径条数 * mid” 。注意判断二分答案跳过K的情况。
DP转移就是正常的选择任意多条不相交路径使答案最大,用 [ 0 / 1 / 2 ] 表示 “未连边” 、 “和孩子连了一条边” 、 “和孩子连了两条边”。
典例剖析3
骑士 https://www.luogu.com.cn/problem/P2607
原题略。
环套树DP,通过断掉一条边变成普通树上DP。
dp[i][0/1]表示以i为根的子树选/不选i号点的最大独立集权值和
处理完所有环外面的DP后,环上随便选一条边
假设最优解里面这条边的两端一共只有三种情况 (选,不选), (不选,不选), (不选,选)
可以枚举这三种情况然后跑三遍DP
或者枚举两个端点中哪个没有被选,跑两遍DP。
例题
https://www.luogu.com.cn/problem/P1099
https://www.luogu.com.cn/problem/P3914
状压DP&记忆化
概述
状压DP是非常常见的DP类型,通过压位记录少量特定信息,来解决一些非多项式问题。
待补充...
例题
https://www.luogu.com.cn/problem/P3959
https://www.luogu.com.cn/problem/P1171
https://www.luogu.com.cn/problem/P3052
https://www.luogu.com.cn/problem/P4460
概率DP
这里不做系统总结。
参考网页
OI-wiki:https://oi-wiki.org/dp/probability/
常见DP优化
概述
NOIP范围内,常见的DP优化方法有:
- 前缀和优化
- 单调队列优化
- 线段树、树状数组优化
待补充...
例题
https://www.luogu.com.cn/problem/P2511
https://www.luogu.com.cn/problem/P2885
https://www.luogu.com.cn/problem/P3572
https://www.luogu.com.cn/problem/P2254
https://www.luogu.com.cn/problem/P5241
树形数据结构

定义及性质
部分简单的性质与定义可以参考上述和OI-Wiki:
https://oi-wiki.org/graph/tree-basic/
补充:
桥:可以简单理解为:一个边为桥当将其删除时,整个图就不是联通的。
完美二叉树:所有叶结点的深度均相同,且所有非叶结点的子结点数量均为2的二叉树称为完美二叉树。
完全二叉树:只有最下面两层结点的度数可以小于2,且最下面一层的结点都集中在该层最左边的连续位置上。
完整二叉树:每个结点的子结点数量均为0或者2的二叉树。换言之,每个结点或者是树叶,或者左右子树均非空。
链: 满足与任一结点相连的边不超过2条的树称为链。
菊花/星: 满足存在u使得所有除u以外结点均与u相连的树称为菊花。
有根二叉树: 每个结点最多只有两个儿子(子结点)的有根树称为二叉树。常常对两个子结点的顺序加以区分,分别称之为左子结点和右子结点。大多数情况下,二叉树一词均指有根二叉树。
树的储存
邻接表
为每个结点𝑢维护一个列表,存储所有与𝑢相邻的结点𝑣。
实现方式:1std::vector或链式前向星。 优点:空间复杂度为𝑂(𝑁)`,遍历一个点的所有邻边效率高。
是存树的标准方法。
链式前向星
struct edge{ll v,w,nx;}e[200010];
ll hd[100010],cnt;
void add(ll u,ll v,ll w){e[++cnt]=(edge){v,w,hd[u]};hd[u]=cnt;}
父亲表示法
使用一个数组parent[N],其中parent[i]存储结点i的父亲结点。
优点:空间复杂度为𝑂(𝑁),查询父节点为𝑂(1)。
缺点:无法直接获取子节点信息,不便于进行DFS、BFS等遍历操作,常用于并查集或作为其他复杂算法的辅助结构。
树的常见搜索
树&DFS
核心思想:沿着一条路径深入,直到末端,然后回溯,选择另一条路径继续深入。
DFS序:
- 定义:在对树进行DFS时,按照访问(进入)结点的顺序记录下来,形成的序列称为DFS序。
- 关键性质:在DFS序中,任意一棵子树的所有结点都占据了连续的一个区间。
- 应用:此性质可将子树问题转化为序列区间问题,便于使用线段树、树状数组等数据结构进行维护
求DFS序代码:
int hd[100010],cnt;
int sz[100010];//子树大小
struct node{int v,nx;}e[200010];//链式前向星存树
int dfn[100010],t;//DFS序
void dfs(int u,int fa){
dfn[u]=++t;
sz[u]=1;
for(int i=hd[u];i;i=e[i].nx){
int v=e[i].v;
if(v==fa)continue;
dfs(v,u);
sz[u]+=sz[v];
}
}
那么𝑢的子树占据的DFS序区间就是[dfn_𝑢,dfn_𝑢+sz_𝑢−1](从dfn_𝑢开始,长为sz_𝑢的一段区间)
典例:
q次操作,每次操作形如𝑢,𝑥,表示把𝑢的子树全部加上𝑥。全部操作结束后,输出每个点的值。
把子树加转化为序列上的区间加即可。具体的,操作𝑢,𝑥变为dfs序上的[dfn_𝑢,dfn_𝑢+sz_𝑢−1]加上𝑥,可以直接转为差分处理。
树&BFS
核心思想:从根结点开始,逐层向下访问。首先访问所有与根直接相连的结点,然后是与这些结点直接相连的未访问结点,以此类推。
实现思路:
- 将起点入队且标记为已访问,其距离设为0。
- 当队列不为空时,取出队首结点
𝑢。 - 若
𝑢为终点𝑡,则其记录的距离即为最短路径长度,算法结束。 - 否则,遍历𝑢的所有未被访问的邻居结点𝑣:
标记
𝑣为已访问。
设置𝑣的距离为𝑢的距离加1。
将𝑣入队。
应用:
-
层次遍历: 按深度从小到大的顺序访问所有结点。
-
无权图最短路: 在树(或任意无权图)中,从
𝑢到𝑣的最短路径长度,等于从𝑢开始BFS,第一次遇到𝑣时的层数。
BFS无权图最短路代码:
int hd[100010],cnt;
struct node{int v,nx;}e[200010];//链式前向星存图
int dis[100010];
bool vis[100010];
queue<int>q;
void bfs(int st){//st是起点
memset(dis,0x3f,sizeof(dis));
dis[st]=0;
q.push(st);
while(!q.empty()){
int u=q.front();q.pop();
if(vis[u])continue;
vis[u]=1;
for(int i=hd[u];i;i=e[i].nx){
int v=e[i].v;
if(dis[v]>dis[u]+1){
dis[v]=dis[u]+1;
q.push(v);
}
}
}
}
二叉树遍历
作为树的特例,二叉树有三种基础的遍历方式,其区别在于根结点的访问时机:
- 先序遍历(Pre-order):根→左子树→右子树
- 中序遍历(In-order):左子树→根→右子树
- 后序遍历(Post-order):左子树→右子树→根
已知中序遍历,配合先序或后序遍历之一,可以唯一确定一棵二叉树的结构。
典例剖析
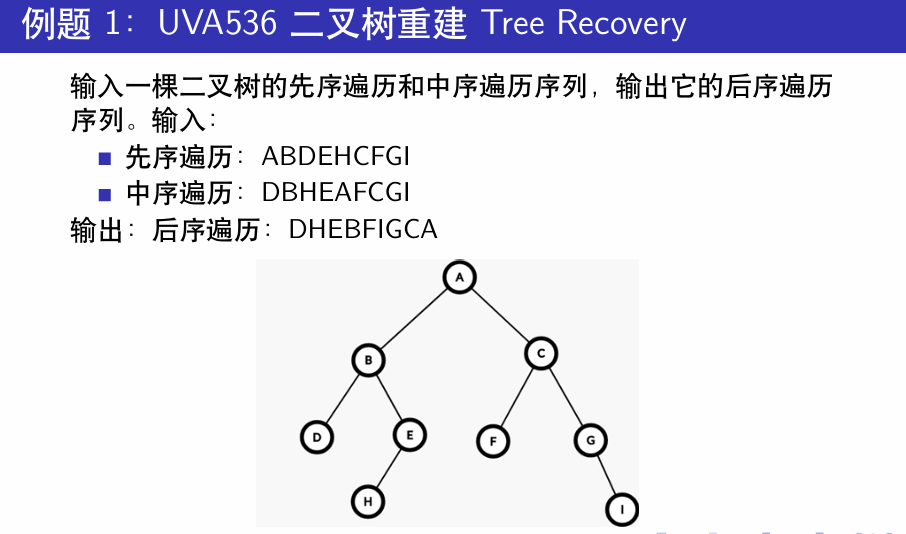
核心思路就是确定遍历中根节点所在的位置。
由前序序列确定当前的根𝑟,然后在根据𝑟在中序遍历中的位置确定左右子树分别包含哪些节点。
确定完后在前序遍历中找到对应序列(容易发现在前序序列中一定是连续的)并递归处理。
核心参考代码:
string s1; // 前序遍历
string s2; // 后序遍历
void calc(int l1,int r1,int l2,int r2) {
// s1 中 [l1,l2] 和 s2 中 [l2,r2] 代表同一棵子树
int m=s2.find(s1[l1]);//找到中序中的根节点
if(m>l2) calc(l1+1,l1+m-l2,l2,m-1);//根节点的左孩子
if(m<r2) calc(l1-l2+m+1,r1,m+1,r2);//右孩子
cout<<s1[l1];//因为是后序遍历,所以放最后;
}
树的直径
定义及性质
定义:树中任意两个结点之间最长的简单路径。
性质:
- 路径的端点必然是叶结点。
- 对于树中任意一点𝑢,离它最远的点𝑣必为某条直径的一个端点。
- 所有直径必相交于一点或一条边。
解法思路
方法一:两次搜索(BFS/DFS)
- 从任意点𝑝出发,通过BFS或DFS找到离它最远的点𝑢;
- 从点𝑢出发,再次通过BFS或DFS找到离它最远的点𝑣;
- 路径(𝑢,𝑣)即为树的一条直径(可以证出,不再赘述)。
方法二:树形动态规划
对于每个结点𝑢,计算经过它的最长路径长度。该路径由分别深入𝑢的两个不同子树的最长链拼接而成。
d[𝑢]表示从𝑢出发,向其子树方向能延伸的最长距离。
转移:𝑑[𝑢]=max𝑣∈𝑠𝑜𝑛(𝑢){𝑑[𝑣]+1}。(边带权类似)
在计算𝑑[𝑢]的过程中,用向下延伸的最长链和次长链更新全局直径答案。
方法1
#include<bits/stdc++.h>
using namespace std;
vector<int>e[100010];
int n;
int dis[100010];
void dfs(int u,int fa){
for(int i=0;i<e[u].size();i++){
int v=e[u][i];if(v==fa)continue;
dis[v]=dis[u]+1;
dfs(v,u);
}
}
int main(){
cin>>n;
for(int i=1;i<=n-1;i++){
int u,v;cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}dfs(1,0);
int r=max_element(dis+1,dis+n+1)-dis;
dis[r]=0;dfs(r,0);
int s=max_element(dis+1,dis+n+1)-dis;
cout<<dis[s];
return 0;
}
方法2
vector<int>e[100010];
int dp[100010][2];
int n,res;
void dfs(int u,int fa){
dp[u][0]=0,dp[u][1]=-0x3f3f3f3f;
for(int i=0;i<e[u].size();i++){
int v=e[u][i];if(v==fa)continue;
dfs(v,u);
if(dp[u][0]<dp[v][0]+1){
dp[u][1]=dp[u][0];
dp[u][0]=dp[v][0]+1;
}
else if(dp[u][1]<dp[v][0]+1){
dp[u][1]=dp[v][0]+1;
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n-1;i++){
int u,v;cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}dfs(1,0);
for(int i=1;i<=n;i++){
res=max(res,dp[i][0]+dp[i][1]);
}cout<<res;
return 0;
}
典例剖析1
给定一棵无根带权树和一个参数
𝑠,要求找出一条路径,使得:
- 这条路径位于一条直径上;
- 这条路径的长度不超过
𝑠;- 树上其他点到这个路径的最大距离最小。
求出这个最小的最大距离,𝑛≤300。
题解:https://www.luogu.com.cn/article/pk09xuo4
典例剖析2
题意同树网的核,其中不要求此路径在一条直径上。
约束范围:n≤3×105
只需要改最后的求答案部分。
int mx=0;
for(int i=1;i<=m;i++)mx=max(mx,d[a[i]]);
int j=1;
for(int i=1;i<=m;i++){
while(j!=m&&c[j+1]-c[i]<=S){
j++;
res=min(res,max(mx,max(c[i],c[m]-c[j])));
}
}
树的重心
定义及性质
定义:
树的重心,也称质心。找到一个结点𝑢,使得删除𝑢及与其相连的边后,剩下若干连通块(子树),其中最大的连通块所含的结点数最小。这个结点𝑢就是树的重心。
性质:
- 删除重心后,最大子树的大小不超过
⌊𝑁/2⌋。 - 一棵树最多有两个重心,且相邻。
- 树的重心到所有其他结点的距离之和最小。
解法及代码
通过一次DFS完成。在DFS回溯阶段,对于当前结点𝑢,我们已经计算出它所有孩子的子树大小size[v]
u的子树大小为size[u] = 1 + sum(size[v])
删除𝑢后,其孩子的子树大小不变,还有一个来自父亲方向
的连通块,大小为𝑁−size[𝑢]
遍历所有结点,计算每个结点作为“最大连通块大小”的候选值,取最小值对应的结点即可。
求重心代码:
vector<int>e[100010];
int n,g,gmx=0x3f3f3f3f;
// g 是重心,gmx 是以重心为根时最大子树的大小。
int sz[100010];// 子树大小
void dfs(int u,int fa){
sz[u]=1;int mx=0;
for(int i=0;i<e[u].size();i++){
int v=e[u][i];if(v==fa)continue;
dfs(v,u);sz[u]+=sz[v];
mx=max(mx,sz[v]);
}mx=max(mx,n-sz[u]);
if(mx<gmx)gmx=mx,g=u;// 如果最大子树更小,更新重心
}
典例剖析
给定一棵有根树,求出每一棵子树(有根树意义下且包含整颗树本身)的重心是哪一个节点。
约束范围:
n≤3×10^5
我们可以先求出𝑢的所有子树的重心,然后对于重子树,从它的重心开始向上枚举每个点并判断是否是重心即可(用最大子树大小不超过一半判断)。
容易发现树上的所有点不会被重复枚举到。因此时间复杂度O(𝑛)
参考代码:
int n,q,fa[N],ans[N],siz[N],son[N];
vector<int>G[N];
void dfs(int x){
int sizz=G[x].size();siz[x]=1;
for(int i=0;i<sizz;i++){
int v=G[x][i];if(v==fa[x])continue;
dfs(v);siz[x]+=siz[v];
if(siz[v]>siz[son[x]])son[x]=v;
}if(siz[son[x]]*2<=siz[x])ans[x]=x;// 重心可能是自身
else{
int xx=ans[son[x]];
while(max(siz[son[xx]],siz[x]-siz[xx])*2>siz[x])xx=fa[xx];
ans[x]=xx;
}
}
LCA(2.0)
定义及性质
定义:在一棵有根树中,对于任意两个结点𝑢,𝑣,它们的最近公共祖先LCA(𝑢,𝑣)是指深度最大的、同时是𝑢和𝑣祖先的结点。
应用场景:
求解树上两点间的路径(𝑢,𝑣)可拆分为(𝑢,LCA(𝑢,𝑣))和(𝑣,LCA(𝑢,𝑣))
是许多树上算法如树上差分的基础构件。
倍增算法

Tarjan算法
高级技巧
树上差分
典例剖析
子树和与倍增
子树和
倍增
典例剖析
上述所有例题
https://www.luogu.com.cn/problem/P2052
https://www.luogu.com.cn/problem/P5588
https://www.luogu.com.cn/problem/P4408
https://www.luogu.com.cn/problem/P5536
https://www.luogu.com.cn/problem/P1395
https://www.luogu.com.cn/problem/P3398
https://www.luogu.com.cn/problem/P5836
https://www.luogu.com.cn/problem/P4427
https://www.luogu.com.cn/problem/P1600
图论
定义及性质
部分简单的性质与定义可以参考上述和OI-Wiki:
https://oi-wiki.org/graph/
图的遍历
BFS
核心思想:从起点开始,按层次由近及远地访问图中的顶点。
数据结构:队列。
过程:
- 起点入队,标记已访问。
- 当队列非空,取出队首顶点𝑢。
- 遍历𝑢的所有未访问邻居𝑣,将其标记并入队。
性质与应用:
保证找到的路径是无权图中的最短路径。
时间复杂度:𝑂(𝑁+𝑀)(邻接表)
代码:
vector<int>e[100010];// vector 存图
bool vis[100010];// 是否已经遍历过
queue<int>q;
void bfs(int s){
q.push(s);
while(!q.empty()){
int u=q.front();q.pop();
if(vis[u])continue;vis[u]=1;
cout<<u<<" ";//BFS 序
for(int i=0;i<e[u].size();i++){
int v=e[u][i];
q.push(v);
}
}
}
DFS
核心思想:沿着一条路径尽可能深地探索,直到末端,然后回溯以探索其他路径。
数据结构:栈,通常通过递归实现(隐式使用调用栈)
过程:
- 从起点开始,标记已访问。
- 对当前顶点𝑢的任一未访问邻居𝑣,递归调用DFS。
- 当𝑢的所有邻居均被访问后,回溯。
应用:
拓扑排序、寻找连通分量、寻找割点与桥等。
时间复杂度:𝑂(𝑁+𝑀)(邻接表)
代码:
vector<int>e[100010];// vector 存图
bool vis[100010];// 是否已经遍历过
queue<int>q;
void dfs(int u){
if(vis[u])return;
cout<<u<<" ";// DFS 序
vis[u]=1;
for(int i=0;i<e[u].size();i++){
int v=e[u][i];
dfs(v);//递归遍历
}
}
典例剖析
查找文献 https://www.luogu.com.cn/problem/P5318
原题略。
简单题,用vector进行存图,储存后对每个vector内部进行排序即可做到先看编号较小的文献。
二分图
定义及性质
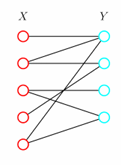
一个无向图𝐺=(𝑉,𝐸)是二分图,当且仅当其顶点集𝑉可以被划分为两个不相交的子集𝑋和𝑌(𝑋∪𝑌=𝑉,𝑋∩𝑌=∅),使得图中的每一条边(𝑢,𝑣)的两个端点都分别属于这两个集合,即𝑢∈𝑋,𝑣∈𝑌 (或反之)。
等价条件:
一个无向图是二分图,当且仅当它不包含奇数环(Odd-lengthCycle)。
例子如图:
判定二分图
判定算法:染色法
基于“不存在奇数环”的性质,我们可以使用BFS或DFS对图进行染色。
过程:
- 初始化所有顶点为未染色状态。
- 遍历所有顶点,若某顶点𝑢未染色,则从𝑢开始进行遍历(BFS/DFS),并将其染为颜色1。
- 在遍历过程中,若从顶点𝑥(颜色𝑐1)访问到邻居𝑦:
若𝑦未染色,则将其染为与𝑥不同的颜色𝑐2。
若𝑦已染色,且颜色与𝑥相同,则说明存在奇数环,该图不是二分图。
- 若遍历完成未发现冲突,则该图是二分图。
时间复杂度:𝑂(𝑁+𝑀)
代码:
int n,m;
vector<int>e[100010];
int col[100010];// 0: 未染, 1: 颜色 1, 2: 颜色 2
bool dfs_dye(int u,int c) {
col[u]=c;
for(int v:e[u]) {
if(!col[v]) {
if(!dfs_dye(v,3-c)) return false;// 3-c 就是换成另一种颜色
}
else if(col[v]==c)return false;
}
return true;
}
int main() {
cin>>n>>m;
for(int i=0; i<m; ++i) {
int u,v;
cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
bool flag=true;
for(int i=1; i<=n; ++i) {
if(!col[i]) {
if(!dfs_dye(i,1)) {
flag=false;
break;
}
}
}
if(flag)cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}
典例剖析
给你一个
𝑁个点𝑀条边的简单无向图𝐺,你需要判定𝐺中是否所有的导出子图都存在点数不少于一半的团。约束范围:多组数据,
𝑁≤105,𝑀 ≤106
我们考虑这张图的补图。此时原命题等价于:对任意点集都存在一个子集,使得该子集构成一个独立集且子集大小不小于点集的一半。其中独立集指的是该集合中的点两两之间没有连边。
可以证明,这个命题等价于这个补图是二分图。
(由于证明过程过长见课件,此处不赘述)
代码:
int n,m;
vector<int>e[100010];
bool vis[100010];
int col[100010];// 0: 未染, 1: 颜色 1, 2: 颜色 2
bool dfs_dye(int u,int c) {
col[u]=c;
for(int v:e[u]) {
if(!col[v]) {
if(!dfs_dye(v,3-c)) return false;// 3-c 就是换成另一种颜色
} else if(col[v]==c)return false;
}
return true;
}
bool mp[3030][3030];//邻接矩阵存原图
bool check() {
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++)if(!mp[i][j]&&i!=j) { //取补图
e[i].push_back(j);
}
}
bool flag=true;
for(int i=1; i<=n; i++) {
if(!col[i]&&!dfs_dye(i,1)) { //判断是否是二分图
flag=false;
break;
}
}
if(flag)cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
有向无环图
定义及性质
一个不存在有向环的有向图称为有向无环图。
- DAG是许多算法模型的基础,如动态规划、任务调度等。
- 描述了对象之间的依赖或偏序关系。
拓扑排序:对一个DAG进行拓扑排序,是将图中所有顶点排成一个线性序列,使得对于图中任意一条边(𝑢,𝑣),顶点𝑢在序列中都出现在顶点𝑣之前。
- 一个图存在拓扑序的充要条件是它是一个DAG;
- 拓扑序通常不唯一。
拓扑排序算法
基于Kahn算法(BFS):
-
计算所有顶点的入度;
-
将所有入度为0的顶点加入一个队列;
-
当队列不为空时:取出队首顶点
𝑢,加入拓扑序列。遍历𝑢的所有出边(𝑢,𝑣),将𝑣的入度减1。若𝑣的入度变为0,则将𝑣入队; -
若最终拓扑序列中的顶点数不等于图的顶点总数
𝑁,则说明图中存在环。
亦可使用DFS实现:拓扑序是各顶点完成DFS(回溯)的逆序。
Kahn(BFS):
int n,m;
vector<int>e[100010];
int in[100010]; // 存储每个点的入度
vector<int>res; // 存储拓扑排序结果
void kahn() {
queue<int>q;
for(int i=1; i<=n; ++i) // 将所有入度为 0 的点入队作为起点
if(in[i]==0)q.push(i);
while(!q.empty()) {
int u=q.front();
q.pop();
res.push_back(u); // 将队首元素加入结果序列
for(int v:e[u]) {
in[v]--; // 将 u 指向的顶点 v 的入度减 1
if(in[v]==0)q.push(v); // 如果 v 的入度变为 0, 则入队
}
}
}
int main() {
cin>>n>>m;
for(int i=0; i<m; ++i) {
int u,v;
cin>>u>>v;
e[u].push_back(v); // 有向边 u->v
in[v]++;
// 顶点 v 的入度加 1
}
kahn();
if(res.size()==n) { // 如果结果序列大小等于顶点数, 则存在拓扑序
for(int i=0; i<res.size(); ++i)cout<<res[i]<<" ";
cout<<endl;
} else cout<<"Graph has a cycle."<<endl;
return 0;
}
另一种方法(DFS):
int n,m;
vector<int>e[100010];
int vis[100010]; // 0: 未访问, 1: 访问中, 2: 已完成
vector<int>res; // 用 vector 模拟栈, 存储拓扑排序结果
bool dfs(int u) {
vis[u]=1; // 标记为“访问中”
for(int v:e[u]) {
if(vis[v]==1)return false; // 遇到“访问中”的邻居, 说明有环
if(vis[v]==0)
if(!dfs(v))return false; // 递归访问, 若下游有环则直接返回
}
vis[u]=2; // 标记为“已完成访问”
res.push_back(u); // 将 u 加入结果集
return true;
}
int main() {
cin>>n>>m;
for(int i=0; i<m; ++i) {
int u,v;
cin>>u>>v;
e[u].push_back(v);
}
bool has_cycle=false;
for(int i=1; i<=n; ++i) { // 遍历所有点, 防止图不连通
if(vis[i]==0)
if(!dfs(i)) {
has_cycle=true;
break;
}
}
if(has_cycle)cout<<"Graph has a cycle."<<endl;
else {
reverse(res.begin(),res.end()); // DFS 得到的是逆拓扑序, 需反转
for(int i=0; i<res.size(); ++i)cout<<res[i]<<" ";
cout<<endl;
}
return 0;
典例剖析
给你一个有向图,点数和边数边数最大
2×105,每个点有一个点权,任选起点,走𝑘步,问经过的点的最大权值最小能是多少?约束范围:
𝑘≤10^18,无解输出-1,没有重边和自环,但是会有环。

int a[200010],U[200010],V[200010];
//边权;原图边
vector<int> e[200010];
int in[200010],dp[200010],top[200010];
// 入度;dp 数组;拓扑序
bool ch(int x) {
//检查是否存在权值 <=x 且长度 >=k 的路径
int mx=0,pp=0,qq=0;
queue<int> q;
for(int i=1; i<=n; i++) {
e[i].clear();
in[i]=0,dp[i]=1;
}
for(int i=1; i<=m; i++) {
int u=U[i],v=V[i];//原图的边
if(a[u]<=x&&a[v]<=x)
//两端点点权都小于等于 x,这条边存在。
e[u].push_back(v),in[v]++;
}
for(int i=1; i<=n; i++)
if(a[i]<=x&&in[i]==0)q.push(i);
djwj233
while(!q.empty()) { //拓扑排序
int u=q.front();
q.pop();
top[++pp]=u;
for(int i=0; i<e[u].size(); i++) {
int v=e[u][i];
if(in[v]>0) {
in[v]--;
if(in[v]==0)q.push(v);
}
}
}
for(int i=1; i<=n; i++)
if(a[i]<=x)qq++;
if(pp!=qq)return true;
//检查环: 存在环,视为无限长路径
//拓扑序上 DP 求最长路
for(int i=pp; i>=1; i--) {
int u=top[i];
for(int j=0; j<e[u].size(); j++) {
int v=e[u][j];
dp[u]=max(dp[u],dp[v]+1);
}
mx=max(mx,dp[u]);
}
if(mx>=k)return true;
return false;
}
最小生成树
定义及性质
给定一个带权的无向连通图𝐺=(𝑉,𝐸,𝑊),生成树是𝐺的一个子图𝑇,它包含了𝐺中所有的顶点𝑉,且本身是一棵树。最小生成树是所有生成树中,边的权值总和最小的那一棵。
对于图的任意一种顶点划分,将其划分为两个集合𝑆和V−𝑆,横跨这两个集合的所有边中,权值最小的那条边必然属于图的某一个MST。
这是Prim和Kruskal算法正确性的基础。
Prim
核心思想:贪心。
从任意一个顶点开始,逐步扩大一棵树,每次选择连接树中顶点与树外顶点的、权值最小的边,并将对应的树外顶点加入树中,直到所有顶点都被包含。

代码:
int n,m;
struct Edge {
int to,w;
};
vector<Edge>e[100010]; // 邻接表存图
bool vis[100010]; // 标记顶点是否已加入 MST
void prim() {
// 优先队列优化 Prim, 存储 {权值, 顶点}, 按权值升序
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>q;
long long mst_w=0;
int node_cnt=0; // 已加入 MST 的顶点数
q.push({0,1}); // 从 1 号点开始, 初始距离为 0
while(!q.empty()&&node_cnt<n) {
int w=q.top().first;
int u=q.top().second;
q.pop();
if(vis[u])continue; // 如果已在 MST 中, 则跳过
vis[u]=true; // 标记 u 加入 MST
mst_w+=w;
node_cnt++;
for(auto& edge:e[u]) { // 遍历 u 的所有邻边
int v=edge.to;
if(!vis[v]) {
q.push({edge.w,v}); // 将未访问的邻居加入队列
}
}
}
if(node_cnt==n)cout<<mst_w<<endl;
else cout<<"orz"<<endl; // orz 代表无法连通
}
Kruskal

代码:
int n,m;
int fa[100010]; // 并查集的父节点数组
struct Edge {
int u,v,w;
bool operator<(const Edge& other)const {
return w<other.w;
}
};
vector<Edge>edges;
int find(int x) { // 并查集查找 (带路径压缩)
return fa[x]==x?x:fa[x]=find(fa[x]);
}
void kruskal() {
sort(edges.begin(),edges.end()); // 将所有边按权值升序排序
for(int i=1; i<=n; ++i)fa[i]=i; // 初始化并查集
long long mst_w=0; // MST 总权值
int edge_cnt=0; // 已选择的边数
for(int i=0; i<m; ++i) {
int u=edges[i].u, v=edges[i].v, w=edges[i].w;
int root_u=find(u);
int root_v=find(v);
if(root_u!=root_v) { // 如果边的两端点不连通
fa[root_u]=root_v; // 合并集合 (连边)
mst_w+=w;
edge_cnt++;
if(edge_cnt==n-1)break; // 边数达到 n-1,MST 已构建完成
}
}
if(edge_cnt==n-1)cout<<mst_w<<endl;
else cout<<"orz"<<endl; // orz 代表无法连通
}
其他:
性质:Kruskal算法生成出来的也是路径最大权最小的生成树。
证明:比较简单:因为我只选取路径权小于Kruskal算法生成树的最大权的边的话,这个图都不连通。
扩展:最大生成树同理,另外,Kruskal算法生成出来的也是路径最小权最大的生成树。
典例剖析
最短路
定义及性质
连通性
有向图的连通性
强连通分量基础
强连通的定义:有向图G强连通是指,G中任意两个结点连通。
强连通分量(SCC)的定义:极大的强连通子图。
强连通:分量内部任意两点互相可达。
极大性:无法再加入原图中的任何一个点来维持这个子图的强连通性质。这个子图在强连通的意义下已经“扩张到了极限”。
强连通分量性质与应用
唯一划分:
任何一个有向图都可以被唯一地划分为若干个强连通分量。
缩点:
如果我们将每个强连通分量看作一个“超级节点”。
然后根据原图的边,在这些“超级节点”之间连边。最终得到的新图是一个有向无环图(DAG)。
应用:
这个性质是解决许多有向图问题的关键。它允许我们将一个复杂的、带环的图问题,转化为一个更简单的、无环的DAG问题,从而可以在DAG上进行拓扑排序、动态规划等操作。
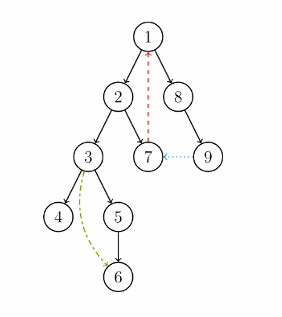
有向图的DFS搜索树
在对有向图进行深度优先搜索时,根据访问情况,图中的边为了方便可以分为四种(如图):
树边:黑色实线,搜索到未访问结点时形成的边。
返祖边:红色虚线(7→1),也称回边,指向当前结点的祖先。
前向边:绿色虚线(3→6),指向当前结点的后代。
横叉边:蓝色虚线(9→7),指向一个已访问过,但并非祖先或后代的结点。
Tarjan算法概述
引入:

求SCC:
核心思想:求解SCC的Tarjan算法,在DFS的基础上,引入了几个核心概念与数据结构。
-
使用
dfn[𝑢]记录时间戳。 -
我们视每个连通分量为搜索树中的一棵子树,在搜索过程中,维护一个栈,每次把搜索树中尚未处理的节点加入栈中。
-
low[𝑢]定义为:从𝑢出发,只经过一条非树边所能到达的、仍在栈中的结点的最小时间戳dfn。
为什么要强调“仍在栈中”?
因为在有向图中,可能存在边指向一个已被访问过、但已确定属于另一个SCC并已出栈的结点。这样的边无法构成一个环路回到当前正在探索的路径上,因此不能用于更新
low值。
感性理解low值的含义:
low[u]的更新来源,结点low[𝑢]是综合以下两种可达路径的最小dfn编号得到的:
- 节点自身的时间戳:
low[𝑢]首先被初始化为dfn[𝑢]因为这本身符合定义。
- 通过其子树或自身的非树边:
对于
𝑢的每个子节点𝑣,low[𝑣]代表了整个子树𝑣能追溯到的最高节点。由于𝑢可以通过树边(𝑢,𝑣)到达子树𝑣的所有路径,因此可以用low[𝑣]来尝试更新low[𝑢]。
本质总结:
low[𝑢]是从节点𝑢开始,通过其DFS子树中的路径,再利用至多一条非树边,所能到达的所有节点中,时间戳dfn最小的那个值。
Tarjan算法

SCC的判定法则:
一个结点𝑢是其所在SCC在DFS树中的“根”(最高点),当且仅当dfn[𝑢]=low[𝑢]
解读:
该条件意味着从𝑢及其子树出发,无法通过任何有向边到达栈中一个比𝑢更早访问的结点。所以,𝑢是它所在SCC中第一个被访问到的点,它构成了这个SCC能在栈中回溯的“最高点”。
操作:
当dfn[𝑢]=low[𝑢]成立时,从栈顶不断弹出结点,直至𝑢被弹出。所有这些弹出的结点共同构成一个SCC。
上述理论的正确性能够被说明,详情见课件。
代码:
int n,m;
vector<int> e[100010];
int tim,dfn[100010],low[100010];//dfs 序;low 数组
int ans[100010],cnt;//ans:这个点属于第几个 scc
int st[100010],tp;//栈
bool in[100010];
int sz[100010];
void dfs(int u) {
dfn[u]=low[u]=++tim;
st[++tp]=u;
in[u]=1;
for(auto v:e[u]) {
if(!dfn[v])
dfs(v),low[u]=min(low[u],low[v]);
else if(in[v])
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]) {
int x;
cnt++;
while(1) {
x=st[tp--];
ans[x]=cnt;
sz[cnt]++;
in[x]=0;
if(x==u)break;
}
}
}
//djwj233
int main() {
cin>>n>>m;
for(int i=1; i<=m; i++) {
int u,v;
cin>>u>>v;
e[u].push_back(v);
}
for(int i=1; i<=n; i++)if(!dfn[i])dfs(i);
return 0;
}
Kosaraju算法
算法思想:
一个概念上更简单、但需要两遍DFS的算法。
-
第一次DFS:在原图
𝐺上任意发起DFS,在函数退出时(回溯时)将结点加入一个栈。这样,栈顶的元素是完成时间最晚的结点。 -
构造反图:构建原图
𝐺的反图𝐺^𝑇,即将𝐺中所有边的方向反转。 -
第二次DFS:按照栈中的顺序(从栈顶到栈底)依次取出结点。如果该结点在
𝐺^𝑇中尚未被访问,就从它开始在𝐺^𝑇上进行一次DFS。每一次DFS遍历所能访问到的所有未访问结点,共同构成一个SCC。
上述算法的合理性可以被证明,详情见课件。
代码:
// g 是原图,g2 是反图
void dfs1(int u) {
vis[u]=true;
for(int v:g[u])
if(!vis[v])dfs1(v);
s.push_back(u);
}
void dfs2(int u) {
color[u]=sccCnt;
for(int v:g2[u])
if(!color[v])dfs2(v);
}
void kosaraju() {
sccCnt=0;
for(int i=1; i<=n; ++i)
if(!vis[i])dfs1(i);
for(int i=n; i>=1; --i)
if(!color[s[i]]) {
++sccCnt;
dfs2(s[i]);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号