算法与数据结构 7 - 斜率优化

引入

斜率优化是一种优化动态规划时间复杂度的优化寄巧，能够极大降低算法的时间复杂度。

斜率优化的一般形式是：

\[f_i=\min /\max \{ a_i \times b_j + c_i + d_j + C\} \]

。

这种状态转移方程暴力计算显然是 \(\mathcal{O}(n^2)\) 的，那么能不能快一些呢？

转化斜率

首先去掉丑陋的 \(\min / \max\)得到：

\[a_i \times b_j + c_i + d_j + C \]

，接着考虑存在决策点 \(j_1,j_2\) 使得 \(j_2\) 优于 \(j_1\)。这里以原式是 \(\min\) 为例。
\(j_2\) 优于 \(j_1\) 的充要条件时

\[a_i \times b_{j_1} + c_i + d_{j_1} + C > a_i \times b_{j_2} + c_i + d_{j_2} + C \]

\[a_i \times b_{j_1} + d_{j_1} > a_i \times b_{j_2} + d_{j_2} \]

。令
\(y_p=d_p\)，\(k'_p=a_p\)，\(x_p=b_p\)，则有

\[k'_i \times x_{j_1} + y_{j_1} > k'_i \times x_{j_2} + y_{j_2} \]

\[y_{j_1} - y_{j_2} > k'_i \times (x_{j_2} - x_{j_1}) \]

\[- k'_i < \frac{y_{j_2} - y_{j_1}}{x_{j_2} - x_{j_1}} \]

可以看到上式形似直线斜率。

数形结合

设 \(k_p=-k'_p\)，则 $$k_i < \frac{y_{j_2} - y_{j_1}}{x_{j_2} - x_{j_1}}$$。将 \((x_p,y_p)\) 看成平面直角坐标系上的决策点。
假设坐标系上存在 \(A\)，\(B\)，\(C\) 三个决策点，考虑将 DP 转移方程变形为 \(f_i - c_i - C = a_i \times b_j + d_j\) 即 \(B_i=k_i \times x_j + y_j\)，\(AB\) 斜率为 \(k_1\)，\(BC\) 斜率为 \(k_2\)。
显然 \(B_i\) 最小时最优。当 \(k_1 > k_2\) 时，
若 \(k_0 > k_1\)，则 \(B\) 优于 \(A\)，否则 \(A\) 优于 \(B\)；若 \(k_0 > k_2\)，则 \(C\) 优于 \(B\)，否则 \(B\) 优于 \(C\)。

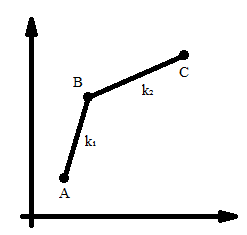
于是有三种情况：

• \(k_0 > k_1 > k_2\)，此时 \(C\) 最优；
• \(k_1 > k_0 > k_2\)，此时 \(A\) 最优；
• \(k_1 > k_2 > k_0\)，此时 \(A\) 最优；
  因此 \(B\) 不可能最优。
  同理可得，当 \(k_1 > k_2\) 时，\(B\) 也不可能最优。
  因此，所有的最优决策点构成上/下凸壳：
  
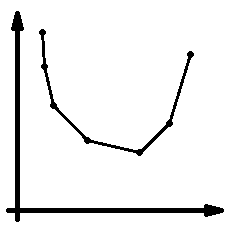
  下文以下凸壳为例。现在需要求出 \(f_i\)，目前已知 \(k_i\)：
  
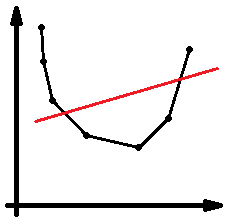
  瞪眼法可看出最优决策点为切线位置：
  
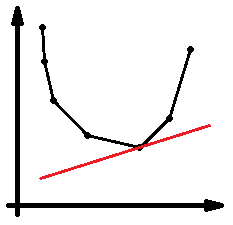
  因此二分即可。计算完毕后向凸壳中插入决策点，可以使用李超树、CDQ 分治和平衡树解决，在此先暂时跳过。

特殊情况

\(k_i\) 、\(x_i\) 单调

因为 \(x_i\) 单调，所以不需要二分求决策点。可以使用单调队列维护决策点集，在查找时直接弹出不合法的决策点，因为被弹出的决策点不再可能被使用。此时由于每个决策点只进队一次，时间复杂度降为 \(\mathcal{O}(n)\)。

\(k_i\) 单调

由于 \(k_i\) 单调，可以二分求插入位置。