《土改》解题报告

目录

  • 题目描述
  • 解题思路
    • 解法一
    • 解法二
  • 参考代码
    • 解法一
    • 解法二

题目描述

土改正在轰轰烈烈地开展，作为优秀党员的小 H 需要帮助 A 村的村民们分配土地。A 村的土地十分狭长，可以把它看成一个数轴，每个人的土地可以看作数轴上的一段区间。 A 村有 \(N\) 位村民，在解放之前，他们就已经有了属于自己的土地。第 \(i\) 位村民的土地为 \((A_i, B_i)\)。由于各种各样的历史问题，可能有一些土地被几位村民同时拥有，但是不会出现一位村民的土地被另一位村民完全包含的情况，也就是对于任意两个不同的 \(i\) 和 \(j\)， 不会存在 \(A_i \le A_j\) 且 \(B_j \le B_i\) 的情况。

小 H 看到 A 村的土地分配十分不均匀而且存在交叉管理的现象，他想重新分配 A 村的土地，使得每位村民的土地长度都相等且任意两个农民的土地不相交。注意到由于村民们不想到不熟悉的地方去种田，因此每位村民新分配的土地必须是他原来土地的子区间。
为了让土地充分被利用，小 H 想让重新分配后每位村民的土地长度尽可能大，请求出最大的土地长度 \(\frac{p}{q}\)，以 p/q 的形式输出（如果答案是整数则 \(q=1\)）。如果误差不超过 \(10^{-6}\) 可以获得该测试点 \(50\) 的分数。

每个测试点 \(T\) 组数据。对于 \(100\%\) 的数据，\(1\le T\le 4\)，\(1\le N\le 10^5\)，\(1\le A_i,B_i \le 10^9\)。

解题思路

解法一

题目中的“误差不超过 \(10^{-6}\) 可以获得该测试点 \(50\) 的分数”在暗示一种求近似解的方法——实数二分。考虑到，如果以 \(x\) 为长度分配土地是可行的，那么以 \(y\) \((0<y<x)\) 为长度分配显然也是可行的。这证明了土地长度的可行性单调，可以进行二分。
现在考虑二分的判断条件——check 函数。该函数需要判断以中间值 mid 为长度的土地是否合法。事先将各区间排序，于是就可以按照顺序依次连接区间。考虑以下两种情况：
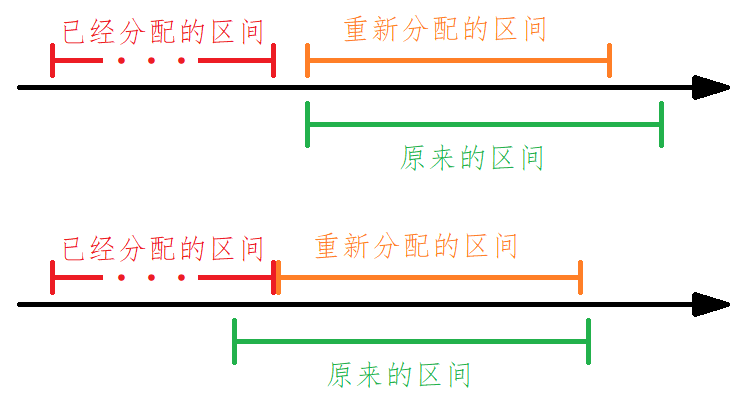
image
现在贪心地考虑划分方案。如果是第一种情况，则直接以原左端点为新左端点，为后面的划分留充足空间；如果是第二种情况，则以已分配的右端点为新左端点，紧贴左侧，同样为他人划分留下空间。而当发现下面这种情况，即时，则说明 mid 值过大，无法分配。于是 check 函数的时间复杂度为 \(\mathcal{O}(n)\)。
image
到目前为止，程序已经可以求出非常接近最大土地长度的一个解。但是由于实数二分无法求出解析解，无法将其写成 \(\frac{p}{q}\) 的形式，因此需要转化。设实际答案为 \(\frac{p}{q}\) 且已化为最简形式，注意到土地被 \(N\) 人平分，所以有 \(1\le q \le N\)。因此，可以分别尝试以 \(1\) 到 \(N\) 作为分母，找到误差最小的一个作为答案。

时间复杂度：排序 \(\mathcal{O}(n \log n)\)，二分 \(\mathcal{O}(n \log n)\)，求分母 \(\mathcal{O}(n)\)。可以通过这道题。

提供者：Eliauk_FP。

Cwkapn 按：这种做法过于逆天，所以赛时没敢写……

解法二

因为新分配土地不能重叠，所以答案应为 $$\min \limits_{i>j} \frac{B_i - A_j}{i - j + 1}$$，请读者仔细思考上式含义。偏移 \(B\) 的下标 \(1\) 位使答案格式变为 \(\min \frac{B_i - A_j}{i - j}\)。
设 \((i,B_i)\) 和 \((j,A_j)\) 为平面直角坐标系上的两个点，则 \(\frac{B_i - A_j}{i - j}\) 为两点连线的斜率。于是考虑维护凸壳，然后二分查找答案。时间复杂度为 \(\mathcal{O}(n \log n)\)。

提供者：Luke_li。

参考代码

解法一：

#include <bits/stdc++.h>
using namespace std;
#define int unsigned long long
const int N = 1e5 + 10;
int n;
struct quj {
	int a, b;
} db[N];
inline bool cmp(const quj &x, const quj &y) {
	return x.a != y.a ? x.a < y.a : x.b < y.b;
}
int gcdll(const int &a, const int &b) {
	if (b == 0) return a;
	return gcdll(b, a % b);
}
bool check(double x) {
	double l = db[1].a;
	for (int i = 1; i <= n; i++) {
		l = max(l, (double)db[i].a);
		if (l + x > db[i].b) return false;
		l += x;
	}
	return true;
}
double dabs(double x) {
	if (x < 0) return -x;
	return x;
}
signed main() {
	#ifndef CWKAPN
	freopen("field.in", "r", stdin);
	freopen("field.out", "w", stdout);
	#endif
	int _;
	cin >> _;
	while (_--) {
		cin >> n;
		for (int i = 1; i <= n; i++) {
			cin >> db[i].a >> db[i].b;
		}
		sort(db + 1, db + n + 1, cmp);
		double l = 1, r = 1e9 + 7;
		while (r - l > 0.0000000001) {
			double mid = (l + r) / 2.0;
			if (check(mid)) l = mid;
			else r = mid;
		}
		int ansp = round(l), ansq = 1;
		double cha = dabs(ansp - l);
		for (int i = 2; i <= n; i++) {
			int tmpp = round(l * i);
			double tcha = dabs(tmpp * 1.0 / i - l);
			if (tcha < cha) {
				cha = tcha;
				ansp = tmpp;
				ansq = i;
			}
		}
		int tmp = gcdll(ansp, ansq);
		ansp /= tmp;
		ansq /= tmp;
		cout << ansp << '/' << ansq << '\n';
	}
	return 0;
}

解法二（Luke_li 提供代码）：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+10;
ll T,n;
struct node
{
	ll l,r;
}a[N];
ll st[N],tot,ansp,ansq;
ll gcd(ll x,ll y)
{
	return y?gcd(y,x%y):x;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	freopen("field.in","r",stdin);
	freopen("field.out","w",stdout);
	cin>>T;
	while(T--)
	{
		ansp=0x3f3f3f3f3f3f3f3f;
		ansq=1;
		cin>>n;
		for(ll i=1;i<=n;i++)
		{
			cin>>a[i].l>>a[i].r;
		}
		sort(a+1,a+n+1,[&](node x,node y){return x.l<y.l;});
		for(ll i=0;i<n;i++)
		{
			a[i].l=a[i+1].l;
		}
		tot=0;
		for(ll i=1;i<=n;i++)
		{
			while(tot>=2 && (a[st[tot]].l-a[st[tot-1]].l)*(i-1-st[tot])<(a[i-1].l-a[st[tot]].l)*(st[tot]-st[tot-1]))
				tot--;
			st[++tot]=i-1;
			ll l=1,r=tot;
			while(r>l)
			{
				ll mid=(l+r+1)>>1;
				assert(mid>1);
				if((a[i].r-a[st[mid]].l)*(st[mid]-st[mid-1])<=(a[st[mid]].l-a[st[mid-1]].l)*(i-st[mid]))
					l=mid;
				else
					r=mid-1;
			}
			if((a[i].r-a[st[l]].l)*ansq<(i-st[l])*ansp)
				ansp=a[i].r-a[st[l]].l,ansq=i-st[l];
		}
		ll gc=gcd(ansp,ansq);
		ansp/=gc;ansq/=gc;
		cout<<ansp<<"/"<<ansq<<endl;
	}
	return 0; 
}
posted @ 2025-04-23 17:16  cwkapn  阅读(30)  评论(0)    收藏  举报