离散数学与结构 Part1

简单集合论

Cantor-Bernstein 定理：两集合互有单射，则必有双射

对于集合 \(S,T\) ，如果存在单射 \(f:S\rightarrow T\) 和 \(g:T\rightarrow S\) ，则 \(S,T\) 之间存在双射。

证明：可以构造一个二分图，左部是 \(S\) ，右部是 \(T\) ，那么图是由环和链构成，其中链没有终点，只有起点。

于是对于从 \(T\) 开始的链，可以令 \(\varphi(x)=g^{-1}(x)\) ，否则令 \(\varphi(x)=f(x)\) 。

环的话就令 \(\varphi(x)=f(x)\) 即可。

Cantor 定理： 不存在 \(2^S\) 到 \(S\) 的单射。

假设 \(\varphi:2^S\rightarrow S\) 是单射。

令 \(A=\varphi(2^S)\) ，\(T=\{x\in A|x\notin \varphi^{-1}(x)\}\) 。

那么 \(T\in 2^S\) 。令 \(a=\varphi(T)\)

如果 \(a\in T\) ，则 \(a\notin \varphi^{-1}(a)=T\) ，矛盾

如果 \(a\notin T\) ，则 \(a\in A-T\) ，那么 \(a\in \varphi^{-1}(a)=T\) ，矛盾

综上，不存在这样的 \(\varphi\) 。

结论：\(R\sim 2^N\)

先找 \(2^N\rightarrow R\) 的单射：令 \(\varphi(S)=\sum\limits_{x\in S}3^{-x}\) 即可。

再找 \(R\rightarrow 2^N\) 的单射，我们分为两步。

先找 \(R\rightarrow (0,1)\) ，其实有 \(R\sim (0,1)\) ，构造 \(f:(0,1)\rightarrow R\) 满足 \(f(x)=\tan(\frac{\pi}{2}(2x-1))\) ，这是双射。

再找 \((0,1)\rightarrow 2^N\) ，考虑把一个 \((0,1)\) 间的数看成是二进制小数，问题在于它有两种表示方式：无限 \(0\) 结尾，无限 \(1\) 结尾，限制为前者即可。

结论：\(N\sim Q\)

\(N\rightarrow Q\) 显然。

\(Q\rightarrow Z×N\) ：把一个有理数写成整数除以正整数的形式。

\(Z×N\rightarrow N\) ： 我们只需要把这些数对按照一个顺序排列，依次编号。可以蛇形地进行编号，虽然最后的形式比较丑，但确实很对。

基数乘幂规则：\((S^T)^W\sim S^{T×W}\)

考虑 \(h:W\rightarrow S^T\) 。现在构造 \(\varphi(h):T×W\rightarrow S\) 。考虑 \(\varphi(h)(x,y)=h(y)(x)\) 即可。这个显然是双射。

结论：\(A\sim A',B\sim B'\rightarrow A^B\sim A'^{B'}\)

对于 \(h:B\rightarrow A\) ，构造 \(\varphi(h):B'\rightarrow A'\) 满足 \(\varphi(h)(b')=(h(b))'\)

结论：\(R^N\sim R\)

\(R\rightarrow R^N\) 显然：对于 \(x\in R\) ，构造 \(f:N\rightarrow R\) 满足 \(f(0)=x,f(1)=0,f(2)=0,\dots\) ，然后令 \(\varphi(x)=f\) 。

\(R^N\rightarrow R\) ：对于 \(f\in R^N\) ，我们可以蛇形串起来 \(f(0),f(1),f(2),\dots\) ，得到一个实数.....。哎，这个构造很魔怔。

另一个证法： \(R^N\sim (2^N)^N\sim 2^{N×N}\sim 2^N\sim R\) 。

---

偏序

\(a\le a,a\le b\land b\le c\rightarrow a\le c,a\le b\land b\le a\rightarrow a=b\)

全序：偏序基础上，任意二者都可比较，也就是 \(a\le b\lor b\le a\)

良序：全序基础上，\(\forall S,\exists a\in S,\forall b\in S,a\le b\)

良序定理

任意集合都能找到一个序，这个序是良序的

连续统假设（CH）

是否有一个集合的势在 \(|N|\) 和 \(|R|\) 之间？前人已经证明：在现有的数学体系下，无法证明这件事是否成立。是，或不是，可以引出两套独立的理论。

命题逻辑

一些符号

原子命题（Atomic Propositions）：\(P,Q,P_1,P_2,\bot,\top,\dots\)

逻辑联结词 (Logical Connectives)：\(\lor,\land,\implies,\iff,\lnot\) ...

辅助符号 (Auxiliary Symbols)：\(()\)...

我们把这个字母表记作 \(\Sigma\) 。

\(\Sigma^{*}=\bigcup\limits_{i=0}^{+\infty}\Sigma^i\) ，表示所有有限字符串的集合。

接下来定义下面的 \(X\subseteq \Sigma^{*}\) 合法：

1. 单独的原子命题都在 \(X\) 中。

2. 如果 \(P,Q\in X\) ，则 \((P\land Q),(P\lor Q),(P\iff Q),(P\implies Q),\dots\in X\)

3. 如果 \(P\in X\) ，则 \((\lnot P)\in X\)

满足上面条件的最小的 \(X\) 被称为 PROP。

比如说 \((P\rightarrow Q)\in PROP\) ，而 \(P\rightarrow Q\notin PROP\) ，但实际上对一个命题我们都默认去掉最外层括号

我们称一个 \(v:PROP\rightarrow \{0,1\}\) 是赋值，定义原子命题的真值表即可

重言式 (tautology) ：对任意赋值 \(v\) ，都有 \([\varphi]_v=1\) 。可以记作 \(\models\varphi\)

\(\Gamma\models \psi\) ：对于任意赋值 \(v\) ，如果 \(\forall \varphi\in \Gamma,[\varphi]_v=1\) ，则 \([\psi]_v=1\)

\(\varphi\models \psi\) ：对于任意赋值 \(v\) ，有 \([\varphi]_v\le [\psi]_v\)

自然演绎（Natural Deduction）

自然演绎系统推导规则：

\(\frac{\varphi\quad \varphi \rightarrow \psi}{\psi}\) ，这被称为假言消去，符号是 \(\rightarrow E\)

\(\frac{\varphi\quad \psi}{\varphi\land \psi}\) ，这被称为合取引入，符号是 \(\land I\)

\(\frac{\varphi \land \psi}{\varphi}\) ，这被称为合取消去，符号是 \(\land E\)

\(\frac{\frac{[\lnot \varphi]}{\bot}}{\varphi}\) ，这是矛盾引入，符号是 RAA

\(\frac{\frac{[\varphi]}{\psi}}{\varphi\rightarrow \psi}\) ，这是蕴含引入，符号是 \(\rightarrow I\)

\(\frac{\bot}{\varphi}\) ，这是爆炸原理

自然演绎具有完备性，也就是说 PROP 里每一条重言式，都能被自然演绎系统证明。

我们来做一个往年期中题。\(r\rightarrow p\vdash ((p\rightarrow q)\rightarrow r)\rightarrow p\)

1. \(r\rightarrow p\) (known)

2. \([(p\rightarrow q)\rightarrow r]\)

3. \([\lnot p]\)

4. \([p]\)

5. \(\bot(3,4,\lnot E)\)

6. \(q(5,\frac{\bot}{\varphi})\)

7. \(p\rightarrow q(5,6,\rightarrow I)\)

8. \(r(2,7,\rightarrow E)\)

9. \(p(1,8,\rightarrow E)\)

10. \(\bot(3,9,\lnot E)\)

11. \(p(3,10,RAA)\)

12. \(((p\rightarrow q)\rightarrow r)\rightarrow p(2,11,\rightarrow I)\)

大概讲一下我的思考过程，首先 \([(p\rightarrow q)\rightarrow r]\) 是显然的，只要接下来能导出 \(p\) 就证完了。

那就反证，\([\lnot p]\) ，有 \(\lnot p\vdash p\rightarrow q\) ，然而这个不是标准步骤，所以得拆开了写。

然后就能通过 \([(p\rightarrow q)\rightarrow r]\) 和 \(p\rightarrow q\) 得到 \(r\) 了。

又有 \(r\rightarrow p\) ，导出 \(p\) ，这和假设矛盾！于是有 \(p\) ，证明结束。

还有另一个往年期中题：\((p\rightarrow q)\rightarrow (\lnot q\rightarrow \lnot p)\) 和 \((\lnot q\rightarrow \lnot p)\rightarrow (p\rightarrow q)\) ，其中哪个能用不带 RAA 的自然演绎证出来？

没有 RAA 其实被称为 直觉主义逻辑 ，它认为双重否定不是肯定。

我们其实还是能用反证法，但只能在 \(\varphi\) 的假设和 \(\bot\) 的基础上，利用 \(\rightarrow I\) 推出 \(\lnot \varphi\) 。

此处只有前者能被证明，证明如下：

\(1.p\rightarrow q \quad 2.[\lnot q] \quad 3.[p] \quad 4.q(2,3,\rightarrow E)\)

\(5.\bot (2,4,\lnot E)\quad 6.\lnot p(3,5,\rightarrow I),7.\neg q\rightarrow \neg p(2,6,\rightarrow I)\)

System K

我们先说明一下 \(\Gamma\Rightarrow \Delta\) 的含义：

对于任意赋值 \(v\) 都有：如果 \(\forall \varphi \in \Gamma,[\varphi]_v=1\) ，则 \(\exists \psi\in \Delta,[\psi]_v=1\) 。

然后有以下八个定理：

---

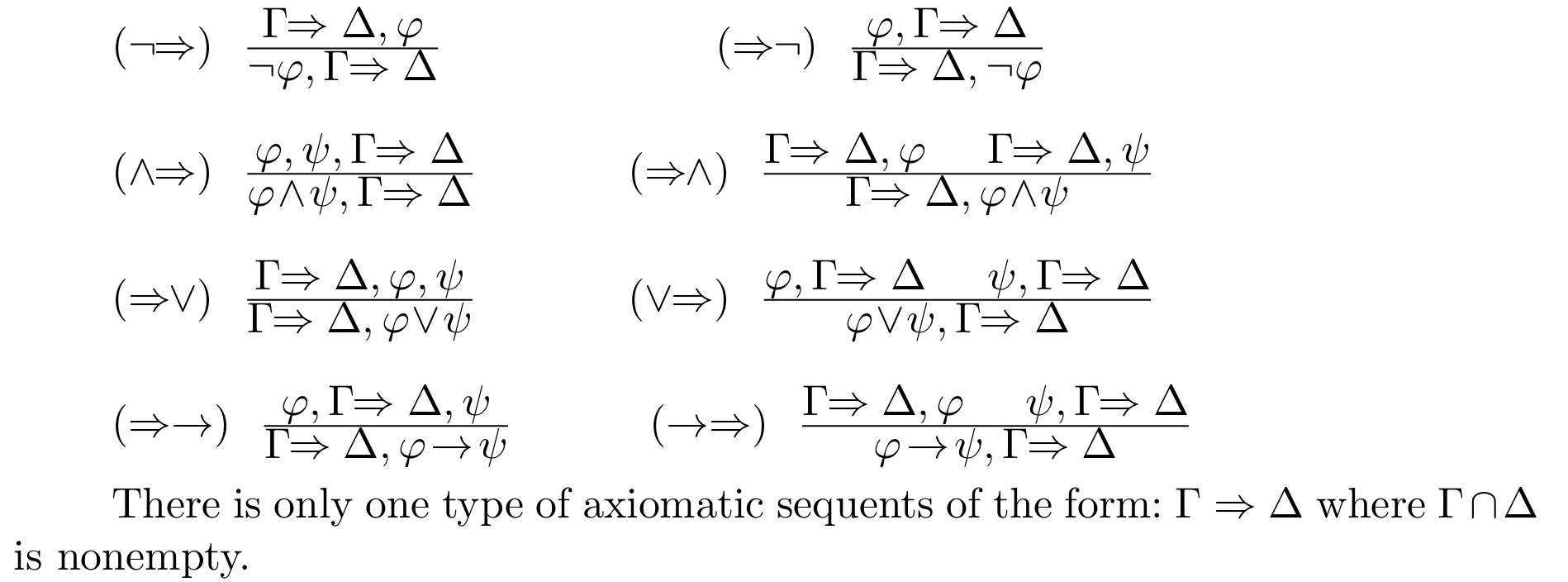
自然演绎的一致性，完备性

\(\Gamma\models \varphi\)

对任意赋值 \(v\) ，如果 \(\forall \psi\in \Gamma,[\psi]_v=1\) ，则 \([\varphi]_v=1\)

\(\Gamma\vdash\varphi\)

对任意赋值 \(v\) ，如果 \(\forall \psi\in \Gamma,[\psi]_v=1\) ，则可以证明 \([\varphi]_v=1\) 。

一致性 (Soundness)

如果 \(\Gamma\vdash\varphi\) 则 \(\Gamma\models \varphi\)

也就是说一个系统所有的规则都是对的。

完备性(Completeness)

如果 \(\Gamma\models \varphi\) 则 \(\Gamma\vdash\varphi\) 。

也就是说啥都能证。

接下来证明自然演绎的完备性。

引理： \(\Gamma,\psi\vdash \varphi\) 且 \(\Gamma,\lnot\psi\vdash \varphi\) ，就能有 \(\Gamma\vdash \varphi\)

那现在想证明 \(\Gamma\vdash\varphi\) ，如果有一个原子命题 \(P_1\) 分别满足 \(\Gamma,P_1\vdash \varphi\) 和 \(\Gamma,\lnot P_1\vdash \varphi\) ，那就结束了。

类似的，我们递归的添加 \(P_2,P_3\) ，直至添加所有原子命题。

对于一个赋值 \(v\) ，令其对应的集合 \(V\) 是： \([P_i]_v=1\) 则把 \(P_i\) 加入 \(V\) ，否则把 \(\lnot P_i\)加入 \(V\) 。

我们只要能证明对任意赋值 \(v\) ，都有 \(\Gamma,V\vdash \varphi\) ，那就结束了。

引理：

对于一个赋值 \(v\) ，若 \([\varphi]_v=1\) 则 \(V\vdash \varphi\) ，否则 \(V\vdash \lnot \varphi\)

引理证明：需要归纳。

\(\varphi\) 是原子命题则显然成立。

\(\varphi=\varphi_1\rightarrow \varphi_2\) ：分类讨论即可。

举个例子，就是说 \(V\vdash \varphi_1,V\vdash \lnot\varphi_2\) 之后能否证明 \(V\vdash \lnot \varphi\) 。

是可以的， \([\varphi_1\rightarrow \varphi_2]\) ，导出 \(\varphi_2\) ，和 \(\lnot \varphi_2\) 形成 \(\bot\) ，于是就有 \(\lnot \varphi\) 了。

其他连接词类似，都用自然演绎来证。

证完引理之后，因为 \(\Gamma\models \varphi\) 在前，本来就有 \([\varphi]_v=1\) ，或者存在 \(\psi\in \Gamma\) 使得 \([\lnot\psi]_v=1\) 。

\([\varphi]_v=1\) 的话，直接就有 \(V\vdash \varphi\) 了。

存在 \([\psi]_v=0\) 的话，就可以导出 \(\bot\) ，从而得到 \(\varphi\) 。也就是说 \(\Gamma,V\vdash\bot\vdash \varphi\)

Predictate Logic（一阶逻辑，谓词逻辑）

字母表：

1. 常元 \(a,b,c,c_1,c_2,\dots\)

2. 变量 \(x,y,z,x_1,x_2,x_3,\dots\)

3. 函数 \(f,g,h,f_1,f_2,f_3,\dots\)

4. 谓词 \(P,Q,P_1,P_2,\dots\)

5. 连接词 \(\land,\to\) 等

6. 辅助词 () 等

7. 量词 \(\forall ,\exists\)

定义 TERM：

\(\forall\) 变量 \(x\) ，\(x\in X\)

\(\forall t_1,t_2,\dots\in X\) 和函数 \(f\) ，\(f(t_1,t_2,\dots)\in X\)

\(\text{TERM}\) 是满足上述条件的最小的 \(X\)。

定义 FOR(formula)：

对于任意谓词 \(P\) 和 terms \(t_1,t_2,\dots\) \(P(t_1\quad t_2)\in X\)

\(\forall \varphi,\psi\in X\) ，\(\varphi\to \psi,\varphi\land \psi\dots\in X\)

\(\forall \varphi\in X\) 和变量 \(x\) ，

\(\forall x\quad \varphi \in X,\exists x\quad \varphi\in X\)

\(\text{FOR}\) 是满足上述条件的最小 \(X\)

定义 Structure：

包含论域 \(\Omega\) ，函数 \(\Omega^n\rightarrow \Omega\) ，谓词 \(P:\Omega^n\rightarrow \{0,1\}\) ，还有常元的对应值。

我的理解：在一个 structure 中，常元和函数的规则就确定了每个 term 在变量赋值后对应 universe 中哪个值。

而 predicate 的规则决定了每个原子公式的 true or false。当然这里也是在 term 中的变量赋值后得到的。

符号记作 \(𝔄\) 。可以把 \(𝔄\) 看做命题逻辑里的 valuation。

对于 \(𝔄\) 的一个函数 \(f\) ，记它对应的那个原本的函数是 \(\overline{f}\) ，那么 \([\overline{f}(t_1,t_2)]_{𝔄}=f([t_1]_𝔄,[t_2]_{𝔄})\)

其他也是类似。

\(\varphi[t/x]\) ：将 \(\varphi\) 中 \(x\) 的所有自由出现替换为 \(t\) 。前提条件：安全性，即替换成 \(t\) 之后，\(t\) 不会因为前面的量词变成 bounded var。

设 \(FV(\varphi)\) 是 \(\varphi\) 中的自由变量集合，\(V(\varphi)\) 是变量集合。

\(𝔄\models \varphi\) 的定义：

若 \(FV(\varphi)=\empty\) ，则 \(𝔄\models \varphi\) 等同于 \([\varphi]_{𝔄}=1\)

否则，我们认为是 \(\forall x_1\forall x_2\dots \varphi\) ，其中 \(x_1,x_2,\dots\) 表示所有 \(FV(\varphi)\) 中的元素

\(𝔄\models \Gamma\) 等价于 \(\forall \varphi\in \Gamma,𝔄\models \varphi\)

\(\Gamma\models \varphi\) ：如果 \(𝔄\models \Gamma\) ,则 \(𝔄\models \varphi\) 。

一阶逻辑中的自然演绎和等号公理

\(\frac{\varphi(x)}{\forall x\varphi(x)}(\forall I)\)

\(\frac{\forall x \varphi(x)}{\varphi(t)}(\forall E)\)

我们认为 \(\exists\) 就是 \(\lnot \forall \lnot\) ，可以想想 \(\forall x\varphi(x)\vdash \exists x \varphi(x)\) 是怎么做的。

等号公理：

\(x=x\)

\(x=y\to y=x\)

\((x=y)\land (y=z)\to x=z\)

\((x_1=y_1)\land(x_2=y_2)\land\dots \to t(x_1,x_2,\dots)=t(y_1,y_2,\dots)\)

皮亚诺公理（Peano Axiom）

这是一套用来定义自然数的公理，它包含函数 \(+,\cdot,S\) 和零元 \(0\) ，单位元 \(1\) ，其中可以认为 \(S(x)\) 是 \(x\) 的后继

\(\forall x \lnot (S(x)=0)\)

\(\forall x\forall y\quad(S(x)=S(y))\to (x=y)\)

\(\forall x \quad x+0=x\)

\(\forall x\forall y\quad x+S(y)=S(x+y)\)

\(\forall x\quad x\cdot 1=x\)

\(\forall x\forall y\quad x\cdot S(y)=x\cdot y+x\)

\(\varphi(0)\land \forall x \quad\varphi(x)\to \varphi(S(x))\) ，则 \(\forall x\quad\varphi(x)\)

皮亚诺公理加上一阶逻辑本身的公理，就可以在自然数上做一些证明了。比如说证 \(\forall x\quad 0+x=x\),可以想一想

一阶理论(theory) 一个由公理和所有能从公理推导出的定理组成的集合 \(T\)。如果 \(T\vdash \varphi\) ，则 \(\varphi\in T\) 。

亨金性质 一个理论 T 是 henkin theory ，当且仅当所有 \(T\) 中形如 \(\exist x \varphi(x)\) 的句子，都存在常量 \(c\) 使得 \(\varphi(c)\in T\) 。

定义理论的扩张：

如果 \(T_2\) 是 \(T_1\) 的扩张，则 \(T_2\) 使用的语言 (即它的符号，如常量、函数、谓词) 必须包含 \(T_1\) 的所有语言。在 \(T_1\) 中可证的公式，在 \(T_2\) 也是可证的。

保守扩张(conservative extension)

就是说 \(T_2\) 是 \(T_1\) 的扩张，且 \(T_2\) 中所有能被 \(T_1\) 的语言写出的能证明的公式，在 \(T_1\) 也能被证明。

亨金扩张

对于一个给定的理论 \(T\)，它的亨金扩张 \(T_H\)​ 是通过一个系统性的过程构造出来的。这个过程会：

1. 对所有形如 \(∃x\varphi(x)\) 的句子，引入一个新的常量符号 \(c_\varphi\)​。这个 \(c\) 被称为亨金常量。

2. 为每个新引入的常量 \(c_\varphi\)，增加一条新的公理：\(∃xφ(x)→φ(c_\varphi)\)

我们记这样的单步扩张为 \(T^*\) ，可以证明 \(T^*\) 是保守扩张。然后不断这样扩张下去，最终得到的理论就是 \(T\) 的亨金扩张 \(T_H\)​，\(T_H\) 显然是 henkin theory。

接下来对 \(T_H\) 再做一次扩展：枚举 \(T_H\) 的语言能写出的所有命题 \(\varphi\) ，如果 \(\varphi,\lnot\varphi\notin T_H\) ，则 \(T_H,\varphi\) 一定不会导出 bot，所以把 \(\varphi,\lnot\varphi\) 二者任取一加入 \(T_H\) ，得到一个新的理论 \(T_{MC}\) 。

接下来可以构造一个 model \(M\) 。

注意这里我们定义了 model ，它是一个特殊的 structure ，如果 \(M\) 是 \(T\) 的 Models，则 \(\forall \varphi\in T\) ，\(\varphi^M=1\) 。其实在命题逻辑里也有一个定义完全一样的相对于 valuation 的 model，但我们之前没提到。

对于 \(T_{MC}\) ，我们首先定义 closed terms，它是指无变量的 terms 。

我们可以在 closed terms 之间定义一个等价关系，即 \(a\sim b\leftrightarrow a=b\in T_{MC}\) 。基于等号公理，可以证明它确实是等价关系。

比如说对于一个包含了自然演绎和皮亚诺公理的理论，我们会认为 \(S(0)+S(0)\) 和 \(S(S(0))\) 在一个等价类，毕竟 \(1+1=2\) （虽然证明不平凡）

然后我们认为 \(M\) 的论域是这些等价类构成的集合。比如一个只包含自然演绎和皮亚诺公理的理论，它在这个定义下的论域其实就是自然数集合。

继续我们的定义，对于常量，\(c^M=[c]\) ，对于函数，\(f^M([x_1],[x_2],\dots,[x_m])=[f(x_1,x_2,\dots,x_m)]\) 。对于谓词，\(P^M([x_1],[x_2],\dots,[x_m])\) 成立当且仅当 \(P(x_1,x_2,\dots,x_m)\in T_{MC}\)

那这个模型有啥用？ 由于 \(T_{MC}\) 是 \(T\) 的一系列保守扩张， 可以证明 \(M\) 是 \(T\) 的一个模型。

于是我们证明了 哥德尔完备性定理 ：经典一阶逻辑中的任意一个一致的理论都能找到一个模型。

然后它有一个等价的结论：\(T\vdash \varphi\leftrightarrow T\models \varphi\) ，其中 \(T\models \varphi\) 代表它的任意模型 \(M\) 有 \(M\models \varphi\) 。

（说实话，我这里肯定是没完全搞懂证明过程的，只是大致记录了老师和 gemini 在说什么，可能也没记录对）

集合论

Axiom of Extensionality (外延性公理)

\(\forall x,y(\forall \delta\quad\delta\in x\leftrightarrow\delta\in y)\) 则 \(x=y\)

Axiom schema of specification （分离公理模式）

对任意谓词 \(\varphi\)

\(\forall A\exists B\forall x(x\in B\leftrightarrow x\in A\land \varphi(x))\)

这是为了定义 \(y_\varphi=\{\delta\in x|\varphi(\delta)\}\)

当然这个谓词可能会加入更多 terms，原理是一样的

Axiom of pairing 配对公理

这是为了定义 \(\delta=\{x,y\}\)

$\forall x,y\exists \delta $ 使得 \(x\in \delta\) 且 \(y\in\delta\)

Axiom of union 并集公理

这是为了定义 \(\cup\)

\(\forall x\exists y\forall w,\delta (\delta\in x\land w\in\delta\to w\in y)\)

Axiom of power set 幂集公理

这是为了定义 \(y=2^x\)

\(\forall x\exists y \forall z(z\subseteq x \to z\in y)\)

Axiom of infinity 无穷公理

\(\exists N (\empty\in N\land (\forall y,y\in N\to y\cup \{y\}\in N))\)

Axiom Schema of Replacement 替换公理模式

这是为了定义 \(B=f_w(A)\)

对任意函数关系 \(\varphi(x,y)\) ，有 \(\forall x\exists y\forall a(a\in y\leftrightarrow \exists b\in x,\varphi(b,a))\)

Axiom of Regularity 正则公理

\(∀A(A\neq\empty\to \exists x(x\in A\land x\cap A=\empty))\)

Axiom of Choice 选择公理

\(\forall S(\forall x\quad x\in S\to x\neq\empty\land\forall x,y(x\in S\land y\in S)\to x\land y=\empty)\)

则 \(\exists T \forall x\quad x\in S\to \exists y\quad y\in S\cap T\)

直观来说，就是说如果有若干个苹果袋子构成了一个集合，则保证你能构造一个袋子，它能在每个袋子中都取一个苹果。

（这里的苹果，袋子其实都是集合）

现在我们证明哥德尔不完备定理，也就是说：任何无矛盾的公理体系，只要包含初等算术的陈述，则必定存在一个不可判定命题，用这组公理不能判定其真假。

我们希望构造一个语句使得它的含义是：它本身不能被证明

简单来讲，首先对所有语句做一个 encoding，映射到一个自然数，这样就可以把 \(TERM,FOR\) 定义成一个自然数的集合。

自然我们又能定义 \(PROV\) ，表示一个理论能证出来的自然数的集合。

对角线引理：对任意一个带一个自由变元的算术公式 \(\psi(x)\) ，都存在 \(\varphi\) 使得 \(PA\vdash \varphi\leftrightarrow \psi(id(\varphi))\)

所以令 \(\psi=\lnot PROV\) ，即可找到一个语句 \(\varphi\) 使得 \(\varphi\leftrightarrow\lnot PROV(id(\varphi))\) 。这个 \(\varphi\) 就是我们想要的东西了。

最后可以证明 \(\varphi\) 和 \(\lnot \varphi\) 都不可能在 \(PROV\) 中，证明就结束了，细节我懒得管了。

初等数论

除数，被除数，余数：可以证明 \(\forall a>0 \forall b\exists!q,r\) 使得 \(b=aq+r\) 且 \(r\in \{0,1,\dots,q-1\}\) ，这可以固定 \(a\) ，对 \(b\) 归纳证明。

\(\text{Prime}(n)\) 可以看做 \((n\neq 1)\land(\forall a\in \N\quad a|n\to (a=1\lor a=n))\)

\(\gcd(a,b)\) ：最大的正整数 \(k\) 使得 \(k|a\) 且 \(k|b\)

特别的，\(\gcd(0,n)=n\)

\(gcd'(a,b)\) ：最小的 \(am+bn\in \Z^+\) ，其中 \(m,n\in \Z\) 。

我们证明 \(gcd'(a,b)=gcd(a,b)\) ：考虑 exgcd 即可

质因数分解(Factorization)：\(n=p_1p_2\dots p_t\) 可以证明分解是唯一的：

归纳证明，对于 \(n\) 的两组分解 \(p_1p_2\dots p_t\) 和 \(q_1q_2\dots q_s\) ，我们首先说明 \(q_1,q_2,\dots,q_s\) 中至少有一个被 \(p_1\) 整除：

反证，由于 \(gcd(a,b)=1\land gcd(a,c)=1\to gcd(a,bc)=1\) ，发现 \(p_1\nmid q_1,p_1\nmid q_2\dots\) 能导出 \(p_1\nmid n\) ，这就矛盾了

不妨设 \(p_1|q_1\) ，因为它们都是质数所以 \(p_1=q_1\) ，根据归纳，剩下的部分的分解是唯一的，这就证完了

同余：\(a\equiv b \pmod m\) 表示 \(m|a-b\)

\(\exists a\) 使得 \(ac\equiv 1\pmod m\) 等价于 \(\gcd(c,m)=1\)

我们称 \(\Z_m^*\) 是 \(\{n\in \Z_m|\gcd(n,m)=1\}\)

费马小定理： \(x^p\equiv x \pmod p\)

对于任意正整数，则有 \((x,n)=1\to x^{\varphi(n)}\equiv 1\pmod n\) ，其中 \(\varphi(n)=|\Z_n^*|\)

证明：考察 \(1,2,\dots,p-1\) ，则 \(x,2x,\dots,(p-1)x\) 模 \(p\) 意义下和 \(1,2,\dots,p-1\) 是对应的，所以 \((p-1)!x^{p-1}\equiv (p-1)!\pmod p\)

那么 \(x^{p-1}\equiv 1\pmod p\)

然后再看任意正整数的情况，同样考察 \(A=\prod\limits_{i\in \Z_n^*}i\) 。那么 \(\prod\limits_{i\in Z_n^*}(ix)=A*x^{\varphi(n)}\) ，由于可以建立 \(i\) 和 \(ix\) 之间的双射，即 \(i=(ix^{-1})x\) ，所以

\(A=A*x^{\varphi(n)}\) ，所以 \(x^{\varphi(n)}\equiv 1\pmod n\)

phi 的性质：\(m=\sum\limits_{d|m}\varphi(d)\)

证明很简单：\(m=\sum\limits_{i=1}^m 1=\sum\limits_{d|m}\sum\limits_{i}[gcd(i,m)=d]=\sum\limits_{d|m}\varphi(\frac{m}{d})=\sum\limits_{d|m}\varphi(d)\)

一种加密算法：取 \(N=pq\) ，其中 \(p,q\) 是大质数。考虑信息 \(m\in \Z_N^*\) ，加密成 \(m^e\bmod N\) 。秘钥是 \(d\) 满足 \(ed\bmod \varphi(m)=1\) 。解码： \((m^e)^d\bmod N=m\) 。

CRT

考虑 \(N=n_1n_2\dots n_t\) ，其中 \(n_1,n_2,\dots,n_t\) 是互质的。

设 \(\pi:\Z_n\to \Z_{n_1}*\Z_{n_2}*\dots*\Z_{n_t}\)

满足 \(\pi(a)=(a\bmod n_1,a\bmod n_2,\dots a\bmod n_t)\)

可以证明 \(\pi\) 是双射，为什么呢？

其实就是要搞出来 \(\pi^{-1}(a_1,a_2,\dots,a_t)\) ，只需要设 \(b_i\) 表示 \(\frac{N}{n_i}\) 模 \(n_i\) 的逆元，那么 \(\sum a_ib_i\frac{N}{n_i}\) 满足条件。

利用这个映射其实就可以证明 phi 为啥是积性函数了。