WeetCode4 —— 二叉树遍历与树型DP
一丶二叉树的遍历
1.二叉树遍历递归写法与递归序
了解过二叉树的朋友,最开始肯定是从二叉树的遍历开始的,二叉树遍历的递归写法想必大家都有所了解。
public static void process(TreeNode node) {
if (node == null) {
return;
}
//如果在这里打印 代表前序遍历 ----位置1
process(node.left);
//如果在这里打印中序遍历 ----位置2
process(node.right);
//如果在这里打印 后序遍历 ---位置3
}
process函数在不同的位置进行打印,就实现了不同的遍历顺序。
我们这里引入一个概念递归序 —— 递归函数到达节点的顺序
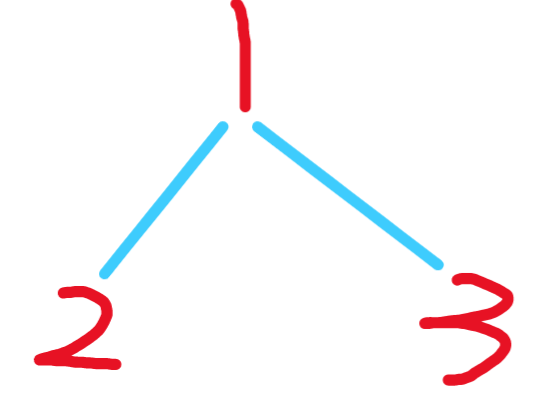
process函数的递归序列是什么呢
- 首先
process(1)此时方法栈记为A,遍历节点1(可以理解为A栈的位置1) - 然后
process(1.left)再开辟一个栈记为B 来到2(可以理解为B栈的位置1) - 接着
process(2.left)为空 出栈 相当于来到了B栈的位置2 ,再次来到2 - 接着
process(2.right)为空,出栈,来到B栈位置3,再次来到2 - 接着出栈,来到A栈位置2
- 然后
process(1.right)再开辟一个栈记为C 来到3(可以理解为C栈的位置1) - 接着
process(3.left)为空 出栈 相当于来到了C栈的位置2 ,再次来到3 - 接着
process(3.right)为空,出栈,来到C栈位置3,再次来到3 - 最后出栈,来到A栈的位置3,来到1
递归序为 1,2,2,2,1,3,3,3,1。可以看到每一个节点都将访问3次。
-
第一次访问的时候打印
1,2,3——先序遍历 -
第二次访问的时候打印
2,1,3——中序遍历 -
第三次访问的时候打印
2,3,1——后序遍历
2.二叉树遍历非递归写法
下面讲解的二叉树遍历非递归写法,都针对下面这棵树

2.1 先序遍历
递归写法告诉我们,打印结果应该是1,2,4,5,3。
对于节点2,我们需要先打印2,然后处理4,然后处理5。栈先进后出,如果我们入栈顺序是4,5 那么会先打印5然后打印4,将无法实现先序遍历,所有我们需要先入5后入4。
- 当前打印的节点记忆为cur
- 打印
- cur的右节点(如果存在)入栈,然后左节点(如果存在)入栈
- 弹出栈顶进行处理,循环往复
程序如下
public static void process1(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stackMemory = new Stack<>();
stackMemory.push(root);
while (!stackMemory.isEmpty()) {
TreeNode temp = stackMemory.pop();
System.out.println(temp.val);
if (temp.right != null) {
stackMemory.push(temp.right);
}
if (temp.left != null) {
stackMemory.push(temp.left);
}
}
}
2.2 中序遍历
-
将树的左边界放入栈中

这时候栈中的内容是
(栈底)1->2->4(栈顶) -
然后弹出节点cur进行打印
也就是打印4,如果cur具备右子树,那么将右子树的进行步骤一
-
循环往复直到栈为空
为什么这可以实现左->中->右打印的中序遍历
首先假如当前节点是A,那么打印A的前提是,左子树打印完毕,在打印A的左子树的时候,我们会把A左子节点的右树入栈,这一保证了打印A之前,A的左子树被处理完毕,然后打印A
打印完A,如果A具备右子树,右子树会入栈,然后弹出,保证了打印完A后打印其右子树,从而实现左->中->右打印的中序遍历
public static void process2(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stackMemory = new Stack<>();
do {
//首先左子树入栈
//1
while (root!=null){
stackMemory.push(root);
root = root.left;
}
//来到这儿,说明左子树都入栈了
//弹出
if (!stackMemory.isEmpty()){
root = stackMemory.pop();
System.out.println(root.val);
//赋值为右子树,右子树会到1的代码位置,如果右子树,那么右子树会进行打印
root = root.right;
}
}while (!stackMemory.isEmpty()||root!=null);
}
2.3 后序遍历
后续遍历就是左->右->头的顺序,那么只要我以头->左->右的顺序将节点放入收集栈中,最后从收集栈中弹出的顺序,就是左->右->头
public static void process3(TreeNode r) {
if (r == null) {
return;
}
//辅助栈
Stack<TreeNode> help = new Stack<>();
//收集栈
Stack<TreeNode> collect = new Stack<>();
help.push(r);
while (!help.isEmpty()) {
TreeNode temp = help.pop();
collect.push(temp);
if (temp.left != null) {
help.push(temp.left);
}
if (temp.right != null) {
help.push(temp.right);
}
}
StringBuilder sb = new StringBuilder();
while (!collect.isEmpty()) {
sb.append(collect.pop().val).append(",");
}
System.out.println(sb);
}
3.二叉树宽度优先遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 (也是宽度优先遍历)即逐层地,从左到右访问所有节点)。
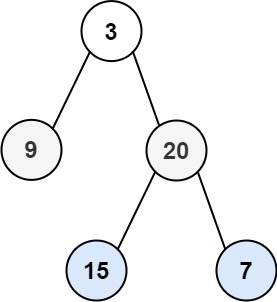
此树宽度优先遍历——[3],[9,20],[15,7]
宽度优先遍历可以使用队列实现,最开始将队列的头放入到队列中,然后当队列不为空的时候,拿出队列头cur,加入到结果集合中,然后如果当前cur的左儿子,右儿子中不为null的节点放入到队列中,循环往复
下面以LeetCode102为例子
public List<List<Integer>> levelOrder(TreeNode root) {
//结果集合
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
//队列
LinkedList<TreeNode> queue = new LinkedList<>();
queue.addLast(root);
//当前层的节点数量为1
int curLevelNum = 1;
while (!queue.isEmpty()) {
//存储当前层节点的值
List<Integer> curLevelNodeValList = new ArrayList<>(curLevelNum);
//下一层节点的数量
int nextLevelNodeNum = 0;
//遍历当前层
while (curLevelNum > 0) {
TreeNode temp = queue.removeFirst();
curLevelNodeValList.add(temp.val);
//处理左右儿子,只要不为null 那么加入并且下一次节点数量加1
if (temp.left != null) {
queue.addLast(temp.left);
nextLevelNodeNum++;
}
if (temp.right != null) {
queue.addLast(temp.right);
nextLevelNodeNum++;
}
//当前层减少
curLevelNum--;
}
//当前层结束了,到下一层
curLevelNum = nextLevelNodeNum;
//存储结果
res.add(curLevelNodeValList);
}
return res;
}
二丶树型DP
1.从一道题开始——判断一颗二叉树是否是搜索二叉树
1.1 中序遍历解题
可以断定我们可以使用中序遍历,然后在中序遍历的途中判断节点的值是满足升序即可
-
递归中序遍历判断是否二叉搜索树
public boolean isValidBST(TreeNode root) { if (root == null) { return true; } //第二个参数记录之前遍历遇到节点的最大值 //由于TreeNode 可能节点值为int 最小使用Long最小 return check(root, new AtomicLong(Long.MIN_VALUE)); } private boolean check(TreeNode node, AtomicLong preValue) { if (node == null) { return true; } //左树是否二叉搜索树 boolean isLeftBST = check(node.left, preValue); //左树不是 那么返回false if (!isLeftBST) { return false; } //当前节点的值 大于之前遇到的最大值 那么更改preValue if (node.val > preValue.get()) { preValue.set(node.val); } else { //不满足升序那么false return false; } //检查右树 return check(node.right, preValue); } -
非递归中序遍历判断是否二叉搜索树
private boolean check(TreeNode root) { if (root == null) { return true; } //前面节点最大值,最开始为null Integer pre = null; Stack<TreeNode> stack = new Stack<>(); do { while (root != null) { stack.push(root); root = root.left; } if (!stack.isEmpty()) { root = stack.pop(); //满足升序那么更新pre if (pre == null || pre < root.val) { pre = root.val; } else { return false; } root = root.right; } } while (!stack.isEmpty() || root != null); return true; }
1.2 引入 —— 树形DP
如果当前位于root节点,我们可以获取root左子树的一些"信息",root右子树的一些信息,我们们要如何判断root为根的树是否是二叉搜索树:
-
root左子树,右子树必须都是二叉搜索树
-
root的值必须大于
左子树最大,必须小于右子树最小 -
根据1和2 我们可以得到
"信息"的结构static class Info { //当前子树的最小值 Integer min; //当前子树最大值 Integer max; //当前子树是否是二叉搜索树 boolean isBst; Info(Integer min, Integer max, boolean flag) { this.min = min; this.max = max; this.isBst = flag; } }
接下来的问题是,有了左右子树的信息,如何拼凑root自己的信息?如果不满足二叉搜索树的要求那么返回isBst为false,否则需要返回root这棵树的最大,最小——这些信息可以根据左子树和右子树的信息构造而来。代码如下
private Info process(TreeNode node) {
//如果当前节点为null 那么返回null
//为null 表示是空树
if (node == null) {
return null;
}
//默认现在是二叉搜索树
boolean isBst = true;
//左树最大,右树最小 二者是否bst ,从左右子树拿信息
Info leftInfo = process(node.left);
Info rightInfo = process(node.right);
//左树不为null 那么 维护isBst标识符
if (leftInfo != null) {
isBst = leftInfo.isBst;
}
//右树不为null 那么 维护isBst标识符
if (rightInfo != null) {
isBst = isBst && rightInfo.isBst;
}
//如果左数 或者右树 不为二叉搜索树 那么返回
if (!isBst){
return new Info(null,null,isBst);
}
//左右是bst,那么看是否满足二叉搜索树的条件
//左边最大 是否小于当前节点
if (leftInfo!=null && leftInfo.max >= node.val){
isBst = false;
}
//右边最小 是否小于当前节点
if (rightInfo!=null && rightInfo.min <= node.val){
isBst = false;
}
//如果不满足 那么返回
if (!isBst){
return new Info(null,null,isBst);
}
//说明node为根的树是bst
//那么根据左右子树的信息返回node这课树的信息
Integer min = node.val;
Integer max = node.val;
if (leftInfo!=null){
min = leftInfo.min;
}
if (rightInfo!=null){
max = rightInfo.max;
}
return new Info(min, max, true);
}
2. 树型DP题目套路
之所以称之为树型DP,是因为这个套路用于解决 树的问题。那么为什么叫DP,这是由于node节点的信息,来自左右子树的信息,类似于动态规划中的状态转移。
2.1树型DP可以解决什么问题

怎么理解:
对于1中判断是否二叉搜索树的问题,S规则就是以node为根的这棵树是否是二叉搜索树
最终整棵树是否二叉搜索树,是依赖于树中所有节点的——"最终答案一定在其中"
2.2 解题模板

3.题目练习
3.1 二叉树的最大深度
需要的信息只有树的高度,我们可以向左子树获取,高度然后获取右子树的高度,然后二叉高度取max加上1就是当前节点为根的树的高度
public int maxDepth(TreeNode root) {
if(root == null){
return 0;
}
int leftH = maxDepth(root.left);
int rightH = maxDepth(root.right);
return Math.max(leftH,rightH)+1;
}
3.2 判断一颗树是否二叉平衡树
- 需要什么信息:左右树的高度,左右树是否是平衡的
- 怎么根据左右构造当前树的信息:当前高度=max(左右高度)+1 ,当前是否平衡=左平衡右平衡且二者高度差不大于1
/***
* 是否是平衡二叉树
* @return
*/
public static boolean isAVL(TreeNode root) {
return process(root).getKey();
}
public static Pair<Boolean, Integer> process(TreeNode root) {
//当前节点为null 那么是平衡二叉树
if (root == null) {
return new Pair<>(true, 0);
}
//右树
Pair<Boolean, Integer> rightData = process(root.right);
//左树
Pair<Boolean, Integer> leftData = process(root.left);
//右树是否是平衡
boolean rTreeIsAVL = rightData.getKey();
//右树高度
int rHigh = rightData.getValue();
//左树是否平衡
boolean lTreeIsAVL = leftData.getKey();
//左树高度
int lHigh = rightData.getValue();
//当前树是平衡要求:左树平衡 右树平衡 且二者高度差小于1
boolean thisNodeIsAvl = rTreeIsAVL
&& lTreeIsAVL
&& Math.abs(rHigh - lHigh) < 2;
//返回当前树的结果 高度树是左右高度最大+1
return new Pair<>(thisNodeIsAvl, Math.max(rHigh, lHigh) + 1);
}
3.3 判断一棵树是否满二叉树
满二叉树 树的高度h和树节点数目n具备 n = 2的h次方 -1 的特性
- 需要左右树的高度,左右树的节点个数
- 怎么根据左右构造当前树的信息:当前高度=max(左高,右高)+1,当前节点个数=左个数+右个数+1
public static boolean isFullTree(TreeNode root) {
Pair<Integer, Integer> rootRes = process(root);
int height = rootRes.getKey();
int nodeNums = rootRes.getValue();
return nodeNums == Math.pow(2, height)-1;
}
//key 高度 v 节点个数
public static Pair<Integer, Integer> process(TreeNode node) {
if (node == null) {
return new Pair<>(0, 0);
}
Pair<Integer, Integer> rInfo = process(node.right);
Pair<Integer, Integer> lInfo = process(node.left);
int thisNodeHeight = Math.max(rInfo.getKey(), lInfo.getKey()) + 1;
int thisNodeNum = rInfo.getValue() + lInfo.getValue() + 1;
return new Pair<>(thisNodeHeight, thisNodeNum);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号