GTM148 抄书笔记 Part I. (Chapter I~III)

写在最前面的一点闲话

GTM148是我最开始想学习抽象代数时找到的；然而当时的我过于地菜，看不懂一点便丢掉了。直到最近想开始复习抽代，我又重新发现了这本书。然后发现它的内容挺有深度，而且不是我想象的那么难读懂(雾)，于是开坑。
个人认为GTM148不适合初学抽象代数的人看；相比于研究生教材，这本书更像是一本群论字典。想要入门抽象代数的可以左转知乎0003大佬的抽象代数专栏(也是我入门抽象代数的专栏)。
这个系列几乎原封不动地把GTM148上的内容搬了过来(也正所谓“抄书笔记”)。(求轻喷)

---

Contents

• Contents
• Chapter I. Groups and Homomorphisms
  • Permutations
  • Cycles
  • Factorization into Disjoint Cycles
  • Even and Odd Permutations
  • Semigroups
  • Groups
  • Homomorphisms
• Chapter II. The Isomorphism Theorems
  • Subgroups
  • Langrange's Theorem
  • Cyclic Groups
  • Normal Subgroups
  • Quotient Groups
  • The Isomorphism Theorems
  • Correspondence Theorem
  • Direct Products
• Chapter III. Symmetric Groups and $G$-Sets
  • Conjugates
  • Symmetric Group
  • The Simplicity of Alternating Groups
  • Some Representation Theorems
  • $G$-Sets
  • Counting Orbits

Chapter I. Groups and Homomorphisms

Permutations

Definition 1.1.1 If $X$ is a nonempty set, a permutation of $X$ is a bijection $\alpha\!:X\rightarrow X$. We denote the set of all permutations of $X$ by $\mathrm S_X$.

In the important special case when $X=\{1,2,\ldots,n\}$, we write $\mathrm S_n$ instead of $\mathrm S_X$. Note that $|\mathrm S_n|=n!$, where $|Y|$ denotes the number of elements in a finite set $Y$.

Remark Given a rearrangement $i_1,i_2,\ldots,i_n$ define a function $\alpha\!:X\rightarrow X$ by $\alpha(j)=i_j$ for all $j\in X$. This function $\alpha$ is an injection because the list has no repetitions; it is a surjection because all of the elements of $X$ appear on the list. Thus, every rearrangement gives a bijection. Conversely, any bijection $\alpha$ can be denoted by two rows:

$$\alpha=\begin{pmatrix}1&2&\ldots&n\\\alpha 1&\alpha 2&\ldots&\alpha n\end{pmatrix},$$

and the bottom row is a rearrangement of $\{1,2,\ldots,n\}$. Thus, the two versions of permutation, rearrangement and bijection, are equivalent. The advantage of the new viewpoint is that two permutations in $\mathrm S_X$ can be "multiplied," for the composite of two bijections is again a bijection.

Cycles

Definition 1.2.1 If $x\in X$ and $\alpha\in\mathrm S_{X}$, then $\alpha$ fixes $x$ if $\alpha(x)=x$ and $\alpha$ moves $x$ if $\alpha(x)\neq x$.

Definition 1.2.2 Let $i_1,i_2,\ldots,i_r$ be distinct integers between $1$ and $n$. If $\alpha\in\mathrm S_{n}$ fixes the remaining $n-r$ integers and if

$$\alpha(i_1)=i_2,\alpha(i_2)=i_3,\ldots,\alpha(i_{r-1})=i_r,\alpha(i_r)=i_1,$$

then $\alpha$ is an $r$-cycle; one also says that $\alpha$ is a cycle of length $r$. Denote $\alpha$ by $\begin{pmatrix}i_1&i_2&\cdots&i_r\end{pmatrix}$.

Every $1$-cycle fixes every element of $X$, and so all $1$-cycles are equal to the identity. A $2$-cycle, which merely interchanges a pair of elements, is called a transposition.

Definition 1.2.3 Two permutations $\alpha,\beta\in\mathrm S_X$ are disjoint if every $x$ moved by one is fixed by the other. In symbols, if $\alpha(x)\neq x$, then $\beta(x)=x$ and if $\beta(y)\neq y$, then $\alpha(y)=y$. A family of permutations $\alpha_1,\alpha_2,\ldots,\alpha_m$ is disjoint if each pair of them is disjoint.

Proposition 1.2.4(the cancellation law for permutations) If either $\alpha\beta=\alpha\gamma$ or $\beta\alpha=\gamma\alpha$, then $\beta=\gamma$.

Proposition 1.2.5 If $\alpha$ and $\beta$ are disjoint permutations, then $\alpha\beta=\beta\alpha$; that is $\alpha$ and $\beta$ commute.

Definition 1.2.6 A permutation $\alpha\in\mathrm S_n$ is regular if either $\alpha$ has no fixed points and it is the product of disjoint cycles of the same length or $\alpha=1$.

Proposition 1.2.7 A permutation $\alpha\in\mathrm S_n$ is regular if and only if $\alpha$ is a power of an $n$-cycle $\beta$; that is, $\alpha=\beta^m$ for some $m$.

Proposition 1.2.8 If $\alpha$ is an $n$-cycle, then $a^k$ is a product of $(n,k)$ disjoint cycles, each of length $n/(n,k)$.

Factorization into Disjoint Cycles

Theorem 1.3.1 Every permutation $\alpha\in\mathrm S_n$ is either a cycle or a product of disjoint cycles.

Proof

The proof is by induction on the number $k$ of points moved by $\alpha$. The base step $k=0$ is true, for then $\alpha$ is the identity. If $k>0$, let $i_1$ be a point moved by $\alpha$. Define $i_2=\alpha(i_1),i_3=\alpha(i_2),\ldots,i_{r+1}=\alpha(i_r)$, where $r$ is the smallest integer for which $i_{r+1}\in\{i_1,i_2,\ldots,i_r\}$. We claim that $\alpha(i_r)=i_1$. Otherwise, $\alpha(i_r)=i_j$ for some $j\ge 2$; but $\alpha(i_{j-1})=i_j$, and this contradicts the hypothesis that $\alpha$ is an injection. Let $\sigma$ be the $r$-cycle $\begin{pmatrix}i_1&i_2&\cdots&i_r\end{pmatrix}$. If $r=n$, then $\alpha$ is the cycle $\sigma$. If $r<n$ and $Y$ consists of the remaining $n-r$ points, then $\alpha(Y)=Y$ and $\sigma$ fixes the points in $Y$. Now $\sigma\big|_{\{i_1,i_2,\ldots,i_r\}}=\alpha\big|_{\{i_1,i_2,\ldots,i_r\}}$. If $\alpha'$ is the permutation with $\alpha'\big|_Y=\alpha\big|_Y$ and which fixes $\{i_1,i_2,\ldots,i_r\}$, then $\sigma$ and $\alpha'$ are disjoint and $\alpha=\sigma\alpha'$. Since $\alpha'$ moves fewer points than does $\alpha$, the inductive hypothesis shows that $\alpha'$, and hence $\alpha$, is a product of disjoint cycles.
■

Definition 1.3.2 A complete factorization of a permutation $\alpha$ is a factorization of $\alpha$ as a product of disjoint cycles which contains one $1$-cycle $(i)$ for every $i$ fixed by $\alpha$.

Theorem 1.3.3 Let $\alpha\in\mathrm S_n$ and let $\alpha=\beta_1\ldots\beta_t$ be a complete factorization into disjoint cycles. This factorization is unique except for the order in which the factors occur.

Proof

Disjoint cycles commute, so that the order of the factors in a complete facatorization is not uniquely determined; however, we shall see that the factors themselves are uniquely determined. Since there is exactly one $1$-cycle $(i)$ for every $i$ fixed by $\alpha$, it suffices to prove uniqueness of the cycles of length at least $2$. Suppose $\alpha=\gamma_1\ldots\gamma_s$ is a second complete factorization into disjoint cycles. If $\beta_t$ moves $i_1$, then $\beta_1^k(i_1)=\alpha^k(i_1)$ for all $k$. Now some $\gamma_j$ must move $i_1$; since disjoint cycles commute, we may assume that $\gamma_j=\gamma_s$. But $\gamma_s^k(i_1)=\alpha^k(i_1)$ for all $k$, and so we have $\beta_t=\gamma_s$. The cancellation law gives $\beta_1\ldots\beta_{t-1}=\gamma_1\ldots\gamma_{s-1}$, and the proof is completed by an induction on $\max\{s,t\}$.
■

Proposition 1.3.4 Let $p$ be a prime and let $\alpha\in\mathrm S_n$. If $\alpha^p=1$, then either $\alpha=1$, $\alpha$ is a $p$-cycle, or $\alpha$ is a product of disjoint $p$-cycles.

Even and Odd Permutations

Theorem 1.4.1 Every permutation $\alpha\in\mathrm S_n$ is a product of transpositions.

Proof

By Theorem 1.3.1
it suffices to factor cycles, and $\begin{aligned}\begin{pmatrix}1&2&\ldots&r\end{pmatrix}=\begin{pmatrix}1&r\end{pmatrix}\begin{pmatrix}1&r-1\end{pmatrix}\ldots\begin{pmatrix}1&2\end{pmatrix}\end{aligned}.$
■

Definition 1.4.2 A permutation $\alpha\in \mathrm S$ is even if it is a product of an even number of transpositions; otherwise, $\alpha$ is odd.

Lemma 1.4.3 If $k,l\ge 0$, then

$$\begin{pmatrix}a&b\end{pmatrix}\begin{pmatrix}a&c&\ldots&c_k&b&d_1&\ldots&d_l\end{pmatrix}=\begin{pmatrix}a&c_1&\ldots&c_k\end{pmatrix}\begin{pmatrix}b&d_1&\ldots&d_l\end{pmatrix}$$

and

$$\begin{pmatrix}a&b\end{pmatrix}\begin{pmatrix}a&c_1&\ldots&c_k\end{pmatrix}\begin{pmatrix}b&d_1&\ldots&d_l\end{pmatrix}=\begin{pmatrix}a&c&\ldots&c_k&b&d_1&\ldots&d_l\end{pmatrix}$$

Definition 1.4.4 If $\alpha\in\mathrm S_n$ and $\alpha=\beta_1\ldots\beta_t$ is a complete factorization into disjoint cycles, then signum $\alpha$ is defined by

$$\operatorname{sgn}(\alpha)=(-1)^{n-t}.$$

It is easy to prove that $\operatorname{sgn}$ is well defined.

Lemma 1.4.5 If $\beta\in\mathrm S_n$ and $\tau$ is a transposition, then

$$\operatorname{sgn}{\tau\beta}=-\operatorname{sgn}(\beta).$$

Proof

Let $\tau=\begin{pmatrix}a&b\end{pmatrix}$ and let $\beta=\gamma _1\cdots\gamma _t$ be a complete factorization of $\beta$ into disjoint cycles. If $a$ and $b$ occur in the same $\gamma$, say, in $\gamma _1$, then $\gamma _1=\begin{pmatrix}a&c_1&\ldots&c_k&b&d_1&\cdots&d_l\end{pmatrix}$, where $k\ge 0$ and $l\ge 0$. By Lemma 1.4.3,

$$\tau\gamma_1=\begin{pmatrix}a&c_1&\cdots&c_k\end{pmatrix}\begin{pmatrix}b&d_1&\cdots&d_l\end{pmatrix},$$

and so $\tau\beta=(\tau\gamma _1)\gamma _2\ldots\gamma _t$ is a complete factorization with an extra cycle. Therefore, $\operatorname{sgn}(\tau\beta)=(-1)^{n-(t+1)}=-\operatorname{sgn}(\beta)$.

The other possibility is that $a$ and $b$ occur in different cycles, say, $\gamma _1=\begin{pmatrix}a&c_1&\ldots&c_k\end{pmatrix}$ and $\gamma _2=\begin{pmatrix}b&d_1&\cdots&d_l\end{pmatrix}$, where $k\ge 0$ and $l\ge 0$. But now $\tau\beta=(\tau\gamma _1\gamma _2)\gamma _3\ldots\gamma _t$, and Lemma 1.4.3 gives

$$\tau\gamma_1\gamma_2=\begin{pmatrix}a&c_1&\cdots&c_k&b&d_1&\cdots&d_l\end{pmatrix}.$$

Therefore, the complete factorization of $\tau\beta$ has one fewer cycle than does $\beta$, and so $\operatorname{sgn}(\tau\beta)=(-1)^{n-(t-1)}=-\operatorname{sgn}(\beta)$.
■

Theorem 1.4.6 For all $\alpha,\beta\in\mathrm S_n$, $\operatorname{sgn}(\alpha\beta)=\operatorname{sgn}(\alpha)\operatorname{sgn}(\beta)$.

Proof

Assume that $\alpha\in\mathrm S_n$ is given and that $\alpha=\tau_1\ldots\tau_m$ is a factorization of $\alpha$ into transpositions with $m$ minimal. We prove, by induction on $m$, that $\operatorname{sgn}(\alpha\beta)=\operatorname{sgn}(\alpha)\operatorname{sgn}(\beta)$ for every $\beta\in\mathrm S_n$. The base step is precisely Lemma 1.4.5. If $m>1$, then the factorization $\tau_2\ldots\tau_m$ is also minimal: if $\tau_2\ldots\tau_m=\sigma_1\ldots\sigma_q$ with each $\sigma_j$ a transposition and $q<m-1$, then the factorization $\alpha=\tau_1\sigma_1\ldots\sigma_q$ violates the minimality of $m$. Therefore, we have

$$\begin{aligned}\operatorname{sgn}&=\operatorname{sgn}(\tau_1\cdots\tau_m\beta)=-\operatorname{sgn}(\tau_2\cdots\tau_m\beta)\qquad&&(\textit{Lemma 1.4.5})\\ &=-\operatorname{sgn}(\tau_2\cdots\tau_m)\operatorname{sgn}(\beta)&&(\textit{by induction})\\ &=\operatorname{sgn}(\tau_1\cdots\tau_m)\operatorname{sgn}(\beta)&&(\textit{Lemma 1.4.5})\\ &=\operatorname{sgn}(\alpha)\operatorname{sgn}(\beta).\end{aligned}$$

■

Theorem 1.4.7

1. A permutation $\alpha\in\mathrm S_n$ is even if and only if $\operatorname{sgn}(\alpha)=1$;
2. A permutation $\alpha$ is odd if and only if it is a product of an odd number of transpositions.

Proposition 1.4.8 $\mathrm S_n$ has the same number of even permutations as of odd permutations.

Semigroups

Definition 1.5.1 A (binary) operation on a nonempty set $G$ is a function $\mu\!: G\times G\rightarrow G$.

Definition 1.5.2 An operation $*$ on a set $G$ is associative if

$$(a*b)*c=a*(b*c)$$

for every $a,b,c\in G$.

Definition 1.5.3 An expression $a_1*a_2*\cdots*a_n$ needs no parentheses if, no matter what choices of multiplications of adjacent factors are made, the resulting elements of $G$ are all equal.

Theorem 1.5.4(Generalized Associativity) If $*$ is an associative operation on a set $G$, then every expression $a_1*a_2*\cdots*a_n$ needs no parentheses.

Definition 1.5.5 A semigroup $(G,*)$ is a nonempty set $G$ equipped with an associative operation $*$.

Definition 1.5.6 Let $G$ be a semigroup and let $\alpha\in G$. Define $a^1=a$ and, for $n\ge 1$, define $a^{n+1}=a*a^n$.

Corollary 1.5.7 Let $G$ be a semigroup, let $a\in G$, and let $m$ and $n$ be positive integers. Then $a^m*a^n=a^{m+n}=a^n*a^m$ and $(a^m)^n=a^{mn}=(a^n)^m$.

Groups

Definition 1.6.1 A group is a semigroup $G$ containing an element $e$ such that:

1. $e*a=a=a*e$ for all $a\in G$;
2. for every $a\in G$, there is an element $b\in G$ with

$$a*b=e=b*a.$$

It is easy to show that $\mathrm S_X$ is a group with composition as operation; it is called the symmetric group on $X$. When $X=\{1,2,\ldots,n\}$, then $\mathrm S_X$ is denoted by $\mathrm S_n$ and is called the symmetric group on $n$ letters.

Definition 1.6.2 A pair of elements $a$ and $b$ in a semigroup commutes if $a*b=b*a$. A group (or a semigroup) is abelian if every pair of its elements commutes.

Examples 1.6.3

1. The set $\mathbb Z$ of all integers is an abelian group with ordinary addition as operation: $a*b=a+b;e=0;-a+a=0$. Some other additive abelian groups are the rational numbers $\mathbb Q$, the real numbers $\mathbb R$, and the complex numbers $\mathbb C$.
2. Recall that if $n\ge 2$ and $a$ and $b$ are integers, then $a\equiv b\pmod n$ means that $n$ is a divisor of $a-b$. Denote the congruence class of an integer $a\text{ mod }n$ by $[a]$; that is,
   $[a]=\{b\in\mathbb Z:b\equiv a\pmod n\}$. The set $\mathbb Z_n$ of all the congruence classes $\text{mod }n$ is called the integers modulo $n$; it is an abelian group when equipped with the operation: $[a]+[b]=[a+b]$; here $e=[0]$ and $[-a]+[a]=[0]$. It is easy to prove that these operations are well defined.
3. If $k$ is a field, then the set of all $n\times n$ nonsingular matrices with entries in $k$ is a group, denoted by $\mathrm{GL}(n,k)$, called the general linear group; here the operation is matrix multiplication, $e$ is the identity matrix $E$, and if $A^{-1}$ is the inverse of the matrix $A$, then $AA^{-1}=E=A^{-1}A$. If $n\ge 2$, then $\mathrm{GL}(n,k)$ is not abelian; if $n=1$, then $\mathrm{GL}(1, k)$ is abelian: it is the multiplicative group $k^{\times }$ of all the nonzero elements in $k$.

Theorem 1.6.4 If $G$ is a group, there is a unique element $e$ with $e*a=a=a*e$ for all $a\in G$. Moreover, for each $a\in G$, there is a unique $b\in G$ with $a*b=e=b*a$.

Proof

Suppose that $e'*a=a=a*e'$ for all $a\in G$. In particular, if $a=e$, then $e'*e=e$. On the other hand, the defining property of $e$ gives $e'*e=e'$, and so $e'=e$.
Suppose that $a*c=e=c*a$, then $c=c*e=c*(a*b)=(c*a)*b=e*b=b$, as desired.
■

As a result of the uniqueness assertions of the theorem, we may now give names to $e$ and to $b$. We call $e$ the identity of $G$ and, if $a*b=e=b*a$, then we call $b$ the inverse of $a$ and denote it by $a^{-1}$.

Corollary 1.6.5 If $G$ is a group and $a\in G$, then $(a^{-1})^{-1}=a$.

Definition 1.6.6 If $G$ is a group and $a\in G$, define the powers of $a$ as follows: if $n$ is a positive integer, then $a^n$ is defined as in any semigroup; define $a^0=e$; define $a^{-n}=(a^{-1})^n$.

Theorem 1.6.7 If $G$ is a semigroup with an element $e$ such that:

1. $e*a=a$ for all $a\in G$;
2. for each $a\in G$ there is an element $b\in G$ with $b*a=e$,

then $G$ is a group.

Proof

We claim that if $x*x=x$ in $G$, then $x=e$. There is an element $y\in G$ with $y*x=e$, and $y*(x*x)=y*x=e$. On the other hand, $y*(x*x)=(y*x)*x=e*x=x$. Therefore, $x=e$.

If $b*a=e$, let us show that $a*b=e$. Now $(a*b)*(a*b)=a*[(b*a)*b]=a*[e*b]=a*b$, and so our claim gives $a*b=e$.

If $a\in G$, we must show that $a*e=a$. Choose $b\in G$ with $b*a=e=a*b$, then we have $a*e=a*(b*a)=(a*b)*a=e*a=a$, as desired.
■

Proposition 1.6.8 Let $G$ be a group, let $a\in G$, and let $m$ and $n$ be relatively prime integers. If $a^m=e$, then there exists $b\in G$ with $a=b^n$.

Proposition 1.6.9 Let $G$ be a group. For each $a\in G$, the functions $L_a\!:G\rightarrow G$, defined by $x\mapsto a*x$ (called left translation by $a$), and $R_a\!:G\rightarrow G$, defined by $x\mapsto x*a^{-1}$ (called right translation by $a$), are bijections.

Proposition 1.6.10 Let $G$ be a group. For all $a,b\in G$, we have $L_{a*b}=L_a\circ L_b$, $R_{a*b}=R_a\circ R_b$, and $L_a\circ R_b=R_b\circ L_a$.

Homomorphisms

Definition 1.7.1
Let $(G,*)$ and $(H,\circ)$ be groups. A function $f\!:G\rightarrow H$ is a homomorphism if, for all $a, b\in G$, we have $f(a*b)=f(a)\circ f(b)$.

An isomorphism is a homomorphism that is also a bijection. We say that $G$ is isomorphic to $H$, denoted by $G\cong H$, if there exists an isomorphism $f\!:G\rightarrow H$.

Theorem 1.7.2 Let $f\!:(G,*)\rightarrow(G',\circ)$ be a homomorphism.

1. $f(e)=e'$, where $e'$ is the identity in $G'$.
2. If $a\in G$, then $f(a^{-1})=f(a)^{-1}$.
3. If $a\in G$ and $n\in\mathbb Z$, then $f(a^n)=f(a)^n$.

Proof

1. Applying $f$ to the equation $e=e*e$ gives $f(e)=f(e*e)=f(e)\circ f(e)$. Now multiply each side of the equation by $f(e)^{-1}$ to obtain $e'=f(e)$.
2. Applying $f$ to the equations $a*a^{-1}=e=a^{-1}*a$ gives $f(a)\circ f(a^{-1})=e'=f(a^{-1})\circ f(a)$. It follows from Theorem 1.6.4, the uniqueness of the inverse, that $f(a^{-1})=f(a)^{-1}$.
3. An easy induction proves $f(a^n)=f(a)^n$ for all $n\ge 0$, and then $f(a^{-n})=f((a^{-1})^n)=f(a^{-1})^n=f(a)^{-n}$.
   ■

Proposition 1.7.3 Let $f\!:X\rightarrow Y$ be a bijection between sets $X$ and $Y$, then $\alpha\mapsto f\circ \alpha\circ f^{-1}$ is an isomorphism $\mathrm S_X\rightarrow \mathrm S_Y$.

Proposition 1.7.4

1. If $f\!:G\rightarrow H$ and $g\!:H\rightarrow K$ are homomorphisms, then so is the composite $g\circ f: G\rightarrow K$.
2. If $f\!:G\rightarrow H$ is an isomorphism, then its inverse $f^{-1}\!:H\rightarrow G$ is also an isomorphism.

Proposition 1.7.5 Let $a$ be a fixed element of a group $G$, define the conjugation by $a$ as $\gamma_a\!:G\rightarrow G$ by $\gamma_a(x)=a*x*a^{-1}$. Then

1. $\gamma_a$ is an isomorphism.
2. If $a,b\in G$, then $\gamma_a\gamma_b=\gamma_{a*b}$.

Proposition 1.7.6

1. A group $G$ is abelian if and only if the function $f\!:G\rightarrow G$, defined by $f(a)=a^{-1}$, is a homomorphism.
2. Let $f\!:G\rightarrow G$ be an isomorphism from a finite group $G$ to itself. If $f$ has no nontrivial fixed points and if $f\circ f$ is the identity function, then $f(x)=x^{-1}$ for all $x\in G$ and $G$ is abelian.

Chapter II. The Isomorphism Theorems

Subgroups

Notation We now drop the $*$ notation for the operation in a group. Henceforth, we shall write $ab$ instead of $a*b$, and we shall denote the identity element by $\mathbf 1$ instead of by $e$.

Definition 2.1.1 A nonempty subset $S$ of a group $G$ is a subgroup of $G$ if $s\in S$ implies $s^{-1}\in S$ and $s,t\in S$ imply $st \in S$.

If $X$ is a subset of group $G$, we write $X\subset G$; if $X$ is a subgroup of $G$, we write $X\le G$.

Theorem 2.1.2 If $S\le G$, then $S$ is a group in its own right.

Theorem 2.1.3 A subset $S$ of a group $G$ is a subgroup if and only if $1\in S$ and $s,t\in S$ imply $st^{-1}\in S$.

Definition 2.1.4 If $G$ is a group and $a\in G$, then the cyclic subgroup generated by $a$, denoted by $\langle a\rangle$, is the set of all the powers of $a$. A group $G$ is called cyclic if there is $a\in G$ with $G=\langle a\rangle$; that is, $G$ consists of all the powers of $a$.

Definition 2.1.5 If $G$ is a group and $a\in G$, then the order of $a$ is $|\langle a\rangle|$, the number of elements in $\langle a\rangle$.

Theorem 2.1.6 If $G$ is a group and $a\in G$ has finite order $m$, then $m$ is the smallest positive integer such that $a^m=\mathbf 1$.

Proof

If $a=\mathbf 1$, then $m=1$. If $a\neq \mathbf 1$, there is an integer $k>1$ so that $\mathbf 1,a,a^2,\ldots,a^{k-1}$ are distinct elements of $G$ while $a^k=a^i$ for some $i$ with $0\le i\le k-1$. We claim that $a^k=\mathbf 1=a^0$. If $a^k=a^i$ for some $i\ge 1$, then $k-i\le k-1$ and $a^{k-i}=\mathbf 1$, contradicting the original list $\mathbf 1, a, a^2, \ldots, a^{k-1}$ having no repetitions. It follows that $k$ is the smallest positive integer with $a^k=\mathbf 1$.

It now suffices to prove that $k=m$; that is, that $\langle a\rangle=\{\mathbf 1,a,a^2,\ldots,a^{k-1}\}$. Clearly $\langle a\rangle\supset\{\mathbf 1,a,a^2,\ldots,a^{k-1}\}$. For the reverse inclusion, let $a^l$ be a power of $a$. By the division algorithm, $l=qk+r$, where $0\le r<k$. Hence, $a^l=a^{qk+r}=a^{qk}a^{r}=a^{r}$, and so $a^{l}=a^{r}\in\{\mathbf 1,a,a^2,\ldots,a^{k-1}\}$.
■

Corollary 2.1.7 If $G$ is a finite group, then a nonempty subset $S$ of $G$ is a subgroup if and only if $s,t\in S$ imply $st\in S$.

Proof

Necessity is obvious. For sufficiency, we must show that $s\in S$ implies $s^{-1}\in S$. It follows easily by induction that $S$ contains all the powers of $s$. Since $G$ is finite, $s$ has finite order, say, $m$. Therefore, $\mathbf 1=s^m\in S$ and $s^{-1}=s^{m-1}\in S$.
■

Example 2.1.8 If $G$ is a group, then $G$ itself and $\{\mathbf 1\}$ are always subgroups. Any subgroup $H$ other than $G$ is called proper, and we denote this by $H<G$; the subgroup $\mathbf 1$ is often called the trivial group.

Definition 2.1.9 Let $f\!:G\rightarrow H$ be a homomorphism, and define
the kernel of $f$ as $\mathrm {ker}f=\{a\in G:f(a)=\mathbf 1\}$ and the image of $f$ as $\mathrm {im} f=\{h\in H:h=f(a)\text{ for some }a\in G\}$.

Proposition 2.1.10 Let $f\!:G\rightarrow H$ be a homomorphism, then $K=\mathrm{ker}f$ is a subgroup of $G$ and $\mathrm{im}f$ is subgroup of $H$.

Theorem 2.1.11 The intersection of any family of subgroups of a group $G$ is again a subgroup of $G$.

Proof

Let $\{S_i:i\in I\}$ be a family of subgroups of $G$. Now $\mathbf 1\in S_i$ for every $i$, and so $\mathbf 1\in\bigcap S_i$. If $a,b\in\bigcap S_i$, then $a,b\in S_i$ for every $i$, and so $ab^{-1}\in S_i$ for every $i$; hence, $ab^{-1}\in\bigcap S_i$, and $\bigcap S_i\le G$.
■

Corollary 2.1.12 If $X$ is a subset of a group $G$, then there is a smallest subgroup $H$ of $G$ containing $X$; that is, if $X\subset S$ and $S\le G$, then $H\le S$.

Definition 2.1.13 If $X$ is a subset of a group $G$, then the smallest subgroup of $G$ containing $X$, denoted by $\langle X\rangle$, is called the subgroup generated by $X$. One also says that $X$ generates $\langle X\rangle$.

In particular, if $H$ and $K$ are subgroups of $G$, then the subgroup $\langle H\cup K\rangle$ is denoted by $H\lor K$.

If $X$ consists of a single element $a$, then $\langle X\rangle=\langle a\rangle$, the cyclic subgroup generated by $a$. If $X$ is a finite set, say, $X=\{a_1,a_2,\ldots,a_n\}$ then we write $\langle X\rangle=\langle a_1,a_2,\ldots,a_n\rangle$ instead of $\langle X\rangle=\langle\{ a_1,a_2,\ldots,a_n\}\rangle$.

Definition 2.1.14 If $X$ is a nonempty subset of a group $G$, then a word on $X$ is an element $w\in G$ of the form

$$w=x_1^{e_1}x_2^{e_2}\ldots x_n^{e_n},$$

where $x_i\in X,e_i=\pm 1$, and $n\ge 1$.

Theorem 2.1.15 Let $X$ be a subset of a group $G$. If $X\neq\varnothing$, then $\langle X\rangle=\mathbf 1$; if $X$ is nonempty, then $\langle X\rangle$ is the set of all the words on $X$.

Proof

If $X=\varnothing$, then the subgroup $\mathbf 1=\{\mathbf 1\}$ contains $X$, and so $\langle X\rangle=\mathbf{1}$. If $X$ is nonempty, let $W$ denote the set of all the words on $X$. It is easy to see that $W$ is a subgroup of $G$ containing $X$ : $\mathbf 1=x_1^{-1}x_1\in W$; the inverse of a word is a word; the product of two words is a word. Since $\langle X\rangle$ is the smallest subgroup containing $X$, we have $\langle X\rangle\subset W$. The reverse inclusion also holds, for every subgroup $H$ containing $X$ must contain every word on $X$. Therefore, $W\le H$, and $W$ is the smallest subgroup containing $X$.
■

Proposition 2.1.16 If $k$ is a field, then the set of all $n\times n$ matrices over $k$ having determinant $1$, denoted by $\mathrm SL(n,k)$, is a subgroup of $\mathrm GL(n,k)$. We call $\mathrm SL(n,k)$ the special linear group over $k$.

Proposition 2.1.17 Let $\mathrm A_n$ be the set of all even permutations in $\mathrm S_n$ (and is also called the alternating group on $n$ letters), then $\mathrm A_n$ is a subgroup with $n!/2$ elements.

Proposition 2.1.18 Suppose that $X$ is a nonempty subset of a set $Y$, then $\mathrm S_X$ can be imbedded in $\mathrm S_Y$; that is, $\mathrm S_X$ is isomorphic to a subgroup of $\mathrm S_Y$.

Proposition 2.1.19 For any $n\ge 2$, $\mathrm S_n$ can be imbedded in $\mathrm A_{n+2}$, but not in $\mathrm A_{n+1}$.

Proposition 2.1.20

1. For any $n\ge 2$, $\mathrm S_n$ can be generated by $(1\ 2),(1\ 3),\ldots,(1\ n)$.
2. For any $n\ge 2$, $\mathrm S_n$ can be generated by $(1\ 2),(2\ 3),\ldots,(i\ i+1),\ldots,(n-1\ n)$.
3. For any $n\ge 2$, $\mathrm S_n$ can be generated by the two elements $(1\ 2)$ and $(1\ 2\ \ldots\ n)$.
4. For any $n> 2$, $\mathrm A_n$ can be generated by all the $3$-cycles.

Langrange's Theorem

Definition 2.2.1 If $S$ is a subgroup of $G$ and if $t\in G$, then a right coset of $S$ in $G$ is the subset of $G$

$$St=\{st:s\in S\}$$

(a left coset is $tS=\{ts:s\in S\}$). One calls $t$ a representative of $St$ (and also of $tS$).

Example 2.2.2 If $G$ is the additive group $\mathbb Z$ of all integers, if $S$ is the set of all multiples of an integer $n$ ($S=\langle n\rangle$, the cyclic subgroup generated by $n$), and if $a\in\mathbb Z$, then the coset $a+S=\{a+qn:q\in\mathbb Z\}=\{k\in\mathbb Z:k\equiv a\pmod n\}$; that is, the coset $a+\langle n\rangle$ is precisely the congruence class $[a]$ of $a\!\!\mod n$.

Lemma 2.2.3 If $S\le G$, then $Sa=Sb$ if and only if $ab^{-1}\in S$ ($aS=bS$ if and only if $b^{-1}a\in S$).

Proof

If $Sa=Sb$, then $a=\mathbf 1a\in Sa=Sb$, and so there is $s\in S$ with $a=sb$; hence, $ab^{-1}=s\in S$. Conversely, assume that $ab^{-1}=\sigma\in S$; hence $a=\sigma b$. To prove that $Sa=Sb$, we prove two inclusions. If $x\in Sa$, then $x=sa$ for some $s\in S$, and so $x=s\sigma b\in Sb$; similarly, if $y\in Sb$, then $y=s'b$ for some $s'\in S$, and $y=s'\sigma^{-1}a\in Sa$. Therefore, $Sa=Sb$.
■

Theorem 2.2.4 If $S\le G$, then any two right (or any two left) cosets of $S$ in $G$ are either identical or disjoint.

Proof

We show that if there exists an element $x\in Sa\cap Sb$, then $Sa=Sb$. Such an $x$ has the form $sb=x=ta$, where $s,t\in S$. Hence $ab^{-1}=t^{-1}s\in S$, and so Lemma 2.2.3 gives $Sa=Sb$.
■

Theorem 2.2.4 may be paraphrased to say that the right cosets of a subgroup $S$ comprise a partition of $G$ (each such coset is nonempty, and $G$ is their disjoint union). This being true, their must be an equivalence relation on $G$ lurking somewhere in the background: it is given, for $a,b\in G$, by $a\equiv b$ if $ab^{-1}\in S$, and its equivalence classes are the right cosets of $S$.

Theorem 2.2.5 If $S\le G$, then the number of right cosets of $S$ in $G$ is equal to the number of left cosets of $S$ in $G$.

Proof

We give a bijection $f\!:\mathscr R\rightarrow\mathscr L$, where $\mathscr R$ is the family of right cosets of $S$ in $G$ and $\mathscr L$ is the family of left cosets. If $Sa\in\mathscr R$, define $f(Sa)=a^{-1}S$, and it can be verified that $f$ is well defined; that is, if $Sa=Sb$, then $a^{-1}S=b^{-1}S$.
■

Definition 2.2.6 If $S\le G$, then the index of $S$ in $G$, denoted by $[G:S]$, is the number of right cosets of $S$ in $G$.

Proposition 2.2.7 In a finite group $G$, one can always choose a common system of representatives for the right and left cosets of a subgroup $S$; if $[G:S]=n$, there exists elements $t_1,\ldots,t_n\in G$ so that $t_1S,\ldots,t_nS$ is the family of all left cosets and $St_1,\ldots,St_n$ is the family of all right cosets.

Definition 2.2.8 If $G$ is a group, then the order of $G$, denoted by $|G|$, is the number of elements in $G$.

Theorem 2.2.9 (Langrange) If $G$ is a finite group and $S\le G$, then $|S|$ divides $|G|$ and $[G:S]=|G|/|S|$.

Proof

By Theorem 2.2.4, $G$ is partitioned into its right cosets

$$G=St_1\cup St_2\cup \ldots \cup St_n,$$

and so $|G|=\sum_{i=1}^n|St_i|$. But it is easy to see that $f_i\!:S\rightarrow St_i$, defined by $f_i(s)=st_i$, is a bijection, and so $|St_i|=|S|$ for all $i$. Thus, $|G|=n|S|$, where $n=[G:S]$.
■

Corollary 2.2.10 If $G$ is a finite group and $a\in G$, then the order of $a$ divides $|G|$.

Definition 2.2.11 A group $G$ has exponent $n$ if $x^n=\mathbf 1$ for all $x\in G$.

Corollary 2.2.12 If $p$ is a prime and $|G|=p$, then $G$ is a cyclic group.

Corollary 2.2.13 (Fermat) If $p$ is a prime and $a$ is an integer, then $a^p\equiv a\pmod p$.

Proof

Let $G=\mathrm U(\mathbb Z_p)$, the multiplicative group of nonzero elements of $\mathbb Z_p$; since $p$ is prime, $\mathbb Z_p$ is a field and $G$ is a group of order $p-1$.

Recall that for integers $a$ and $b$, one has $a\equiv b\pmod p$ if and only if $[a]=[b]$ in $\mathbb Z_p$. If $a\in \mathbb Z$ and $[a]=[0]$ in $\mathbb Z_p$, then it is clear that $[a]^p=[0]=[a]$. If $[a]\neq [0]$, then $[a]\in G$ and so $[a]^{p-1}=[1]$, by Corollary 2.2.10; multiplying by $[a]$ now gives the desired result.
■

Proposition 2.2.14 Let $a\in G$ have order $n=mk$, where $m,k\ge 1$, then $a^k$ has order $m$.

Proposition 2.2.15 If $a\in G$ has order $n$ and $k$ is an integer with $a^k=\mathbf 1$, then $n$ divides $k$. Indeed, $\{k\in\mathbb Z:a^{k}=\mathbf 1\}$ consists of all the multiplies of $n$.

Proposition 2.2.16 If $G$ is a finite group and $K\le H\le G$, then $[G:K]=[G:H][H:K]$.

Proposition 2.2.17 If $a\in G$ has finite order and $f\!:G\rightarrow H$ is a homomorphism, then the order of $f(a)$ divides the order of $a$.

Proposition 2.2.18 Every subgroup of a cyclic group is cyclic.

Proposition 2.2.19 Two cyclic groups are isomorphic if and only if they have the same order.

Proposition 2.2.20 If $G=\langle a\rangle$ is cyclic of order $n$, then $a^k$ is also a generator of $G$ if and only if $(k,n)=1$.

Cyclic Groups

Lemma 2.3.1 If $G$ is a cyclic group of order $n$, then there exists a unique subgroup of order $d$ for every divisor $d$ of $n$.

Proof

If $G=\langle a\rangle$, then $\langle a^{n/d}\rangle$ is a subgroup of order $d$, by Proposition 2.2.14. Assume that $S=\langle b\rangle$ is a subgroup of order $d$. Now $b^d=\mathbf 1$; moreover, $b=a^m$ for some $m$, by Proposition 2.2.15. Then we have $md=nk$ for some integer $k$, and $b=a^m=(a^{n/d})^k$. Therefore, $\langle b\rangle\le\langle a^{n/d}\rangle$, and this inclusion is equality because both subgroups have order $d$.
■

Theorem 2.3.2 A group $G$ of order $n$ is cyclic if and only if, for each divisor $d$ of $n$, there is at most one cyclic subgroup $G$ having order $d$.

Proof

If $G$ is cyclic, then the result is Lemma 2.3.1. For the converse, recall from the previous proof that $G$ is the disjoint union $\bigcup \mathrm {gen}(C)$, where $C$ ranges over all the cyclic subgroups of $G$ and $\mathrm {gen}(C)$ denote the set of all the generators of $C$. Hence, $n=|G|=\sum|\mathrm{gen}(C)|\le\sum_{d|n}\varphi(d)=n$. We conclude that $G$ must have a cyclic subgroup of order $d$ for every divisor $d$ of $n$; in particular, $G$ has a cyclic subgroup of order $d=n$, and so $G$ is cyclic.
■

Theorem 2.3.3 Let $p$ be a prime. A group $G$ of order $p^n$ is cyclic if and only if it is an abelian group having a unique subgroup of order $p$.

Proof

Necessity follows at once from Lemma 2.3.1. For the converse, let $a\in G$ have largest order, say $p^k$ (it follows that $g^{p^k}=\mathbf 1$ for all $g\in G$). Of course, the unique subgroup $H$ of order $p$ is a subgroup of $\langle a\rangle$. If $\langle a\rangle$ is a proper subgroup of $G$, then there is $x\in G$ with $x\notin \langle a\rangle$ but with $x^p\in\langle a\rangle$; let $x^p=a^l$. If $k=1$, then $x^p=\mathbf 1$ and $x\in H\le\langle a\rangle$, a contradiction; we may, therefore, assume that $k>1$. Now

$$\mathbf 1=x^{p^{k}}=(x^p)^{p^{k-1}}=a^{lp^{k-1}},$$

so that $l=pm$ for some integer $m$, by Proposition 2.2.15. Hence, $x^p=a^{mp}$, and so $\mathbf 1=x^{-p}a^{mp}$. Since $G$ is abelian, $x^{-p}a^{mp}=(x^{-1}a^m)^p$, and so $x^{-1}a^m\in H\le\langle a\rangle$. This gives $x\in\langle a\rangle$, a contradiction. Therefore, $G=\langle a\rangle$ and hence is cyclic.
■

Proposition 2.3.4 A subgroup $H< G$ is a maximal subgroup of $G$ if there is no subgroup $N$ of $G$ with $H< N< G$. If $G$ is a finite group with only one maximal subgroup, then $G$ is cyclic.

Normal Subgroups

Definition 2.4.1 If $S$ and $T$ are nonempty subsets of a group $G$, then

$$ST=\{st:s\in S\text{ and }t\in T\}.$$

If $S\le G,t\in G$, and $T=\{t\}$, then $ST$ is the right coset $St$. Notice that the family of all the nonempty subsets of $G$ is a semigroup under this operation: if $S,T$ and $U$ are nonempty subsets of $G$, then $(ST)U=S(TU)$, for either side consists of all the elements of $G$ of the form $(st)u=s(tu)$ with $s\in S,t\in T$, and $u\in U$.

Theorem 2.4.2 If $S$ and $T$ are subgroups of a finite group $G$, then $|ST||S\cap T|=|S||T|$.

Proof

Define a function $\varphi\!:S\times T\rightarrow ST$ by $(s,t)\mapsto st$. Since $\varphi$ is a surjection, it suffices to show that if $x\in ST$, then $|\varphi^{-1}(x)|=|S\cap T|$. We show that $\varphi^{-1}(x)=\{(sd,d^{-1}t)|d\in S\cap T\}$. It is clear that $\varphi^{-1}(x)$ contains the right side. For the reverse inclusion, let $(s,t),(\sigma,\tau)\in\varphi^{-1}(x)$; that is, $s,\sigma\in S$, $t,\tau\in T$, and $st=x=\sigma\tau$. Thus, $s^{-1}\sigma=t\tau^{-1}\in S\cap T$; let $d=s^{-1}\sigma=t\tau^{-1}$ denote their common value. Then $\sigma=s(s^{-1}\sigma)=sd$ and $d^{-1}t=\tau t^{-1}t=\tau$, as desired.
■

Definition 2.4.3 A subgroup $K\le G$ is a normal subgroup, denoted by $K\lhd G$, if $gKg^{-1}=K$ for every $g\in G$.

If $K\le G$ and there are inclusions $gKg^{-1}\le K$ for every $g\in G$, then $K\lhd G$: replacing $g$ by $g^{-1}$, we have the inclusion $g^{-1}Kg\le K$, and this gives the reverse inclusion $K\le gKg^{-1}$.

Proposition 2.4.4 If $K\le H\le G$ and $K\lhd G$, then $K\lhd H$.

Proposition 2.4.5 Let $G$ be a group, then the intersection of any family of normal subgroups of $G$ is itself a normal subgroup of $G$.

Proposition 2.4.6 Let $f\!:G\rightarrow H$ be a homomorphism, then the kernel $\mathrm{ker} f$ is a normal subgroup of $G$.

Definition 2.4.7 If $x\in G$, then a conjugate of $x$ in $G$ is an element of the form $axa^{-1}$ for some $a\in G$; equivalently, $x$ and $y$ are conjugate if $y=\gamma_a(x)=axa^{-1}$ for some $a\in G$.

Proposition 2.4.8 If $S\le G$, then $S\lhd G$ if and only if $\gamma(S)\le S$ for every conjugation $\gamma$.

Proposition 2.4.9 If $S$ is a finite nonempty subset of $G$ with $SS=S$, then $S$ is a subgroup; however, when $S$ is infinite, the statement may be false.

Definition 2.4.10 If $S$ and $T$ are (not necessarily distinct) subgroups of $G$, then an ($S$-$T$)-double coset is a subset of $G$ of the form $SgT$, where $g\in G$.

Proposition 2.4.11 Let $S$ and $T$ be subgroups of $G$, then the family of all ($S$-$T$)-double coset partitions $G$.

Proposition 2.4.12 Let $S$ and $T$ be subgroups of a finite group $G$, and suppose that $G$ is the disjoint union

$$G=\bigcup_{i=1}^nSg_iT,$$

then we have $[G:T]=\sum_{i=1}^n[S:S\cap g_iTg_i^{-1}]$.

Proposition 2.4.13 Let $G$ be a finite group, and let $S$ and $T$ be (not necessarily distinct) nonempty subsets, then either $G=ST$ or $|G|\ge |S|+|T|$ is true.

Proposition 2.4.14 If $S\le G$ and $[G:S]=2$, then $S\lhd G$.

Definition 2.4.15 If $X$ is a subset of $G$, then there is a smallest normal subgroup of $G$ which contains $X$; it is called the normal subgroup generated by $X$, often denoted by $\langle X\rangle^G$.

Proposition 2.4.16 If $X=\varnothing$, then $\langle X\rangle^G=\mathbf 1$; if $X\neq\varnothing$, then $\langle X\rangle^G$ is the set of all words on the conjugates of elements in $X$.

Proposition 2.4.17 If $H$ and $K$ are normal subgroups of $G$, then $H\lor K\lhd G$.

Proposition 2.4.18 If a normal subgroup $H$ of $G$ has index $n$, then $g^n\in H$ for all $g\in G$.

Quotient Groups

Theorem 2.5.1 If $N\lhd G$, then the cosets of $N$ in $G$ form a group, denoted by $G/N$, of order $[G:N]$.

Proof

As operation, we propose the multiplication of nonempty subsets of $G$ defined earlier. We have already observed that this operation is associative. Now

$$\begin{aligned} NaNb&=Na(a^{-1}Na)b\\ &=N(aa^{-1})Nab=NNab=Nab \end{aligned}$$

Thus, $NaNb=Nab$, and so the product of two cosets is a coset. It is easy to prove that the identity is the coset $N=N\mathbf 1$ and that the inverse of $Na$ is $N(a^{-1})$.
■

Corollary 2.5.2 If $N\lhd G$, then the natural map (i.e., the function $\nu\!:G\rightarrow G/N$ defined by $\nu(a)=Na$) is a surjective homomorphism with kernel $N$.

As for the integer group $\mathbb Z$, the quotient group $\mathbb Z/\langle n\rangle$ is equal to $\mathbb Z_n$, the group of integers modulo $n$. An arbitrary quotient group $G/N$ is often called $G\!\!\mod N$ because of this example.

Proposition 2.5.3 Let $H\lhd G$, let $\nu\!:G\rightarrow G/H$ be the natural map, and let $X\subset G$ be a subset such that $\nu(X)$ generates $G/H$, then $G=\langle H\cup X\rangle$.

Definition 2.5.4 If $a,b\in G$, the commutator of $a$ and $b$, denoted by $[a,b]$, is

$$[a,b]=aba^{-1}b^{-1}.$$

The commutator subgroup (or derived subgroup) of $G$, denoted by $G'$, is the subgroup of $G$ generated by all the commutators.

Theorem 2.5.5 The commutator subgroup $G'$ is a normal subgroup of $G$. Moreover, if $H\lhd G$, then $G/H$ is abelian if and only if $G'\le H$.

Proof

If $f\!:G\rightarrow G$ is a homomorphism, then $f(G')\le G'$ because $f([a,b])=[fa,fb]$. It follows from Proposition 2.4.8 that $G'\lhd G$.

Let $H\lhd G$. If $G/H$ is abelian, then $HaHb=HbHa$ for all $a,b\in G$; that is, $Hab=Hba$, and so $ab(ba)^{-1}=aba^{-1}b^{-1}=[a,b]\in H$. Thus we have $G'\le H$. Conversely, suppose that $G'\le H$. For every $a,b\in G$, we have $ab(ba)^{-1}=[a,b]\in G'\le H$, and so $Hab=Hba$; that is, $G/H$ is abelian.
■

Proposition 2.5.6 Let $x,y\in G$ and assume that both $x$ and $y$ commute with $[x,y]$. Then:

1. $[x,y]^n=[x^n,y]=[x,y^n]$ for all $n\in\mathbb Z$;
2. $(xy)^n=[y,x]^{n(n-1)/2}x^ny^n$ for all $n\ge 0$.

Proposition 2.5.7 If $x,y,z\in G$, denote $yxy^{-1}$ by $x^y$ and $[x,[y,z]]$ by $[x,y,z]$.

1. we have $[x,yz]=[x,y][x,z]^y$ and $[xy,z]=[y,z]^x[x,z]$.
2. Jacobi identity $[x,y^{-1},z]^y[y,z^{-1},x]^z[z,x^{-1},y]^{x}=\mathbf 1$.

Proposition 2.5.8 Let $H,K,L$ be subgroups of $G$ and let $[H,K,L]=\langle[h,k,l]:h\in H,k\in K,l\in L\rangle$.

1. Three subgroups lemma If $N\lhd G$ and $[H,K,L][K,L,H]\le N$, then $[L,H,K]\le N$.
2. If $H,K$ and $L$ are all normal subgroups of $G$, then $[L,H,K]\le [H,K,L][K,L,H]$.

The Isomorphism Theorems

Theorem 2.6.1 (First Isomorphism Theorem) Let $f\!:G\rightarrow H$ be a homomorphism with kernel $K$. Then $K$ is a normal subgroup of $G$ and $G/K\cong \mathrm{im}f$.

Proof

We have already noted that $K\lhd G$. Define $\varphi: G/K\rightarrow H$ by $\varphi(Ka)=f(a)$. To see that $\varphi$ is well defined, assume that $Ka=Kb$; that is, $ab^{-1}\in K$. Then $\mathbf 1=f(ab^{-1})=f(a)f(b)^{-1}$, and $f(a)=f(b)$; it follows that $\varphi(Ka)=\varphi(Kb)$, as desired. Now $\varphi$ is a homomorphism:

$$\varphi(KaKb)=\varphi(Kab)=f(ab)=f(a)f(b)=\varphi(Ka)\varphi(Kb).$$

It is plain that $\mathrm {im}\varphi=\mathrm {im} f$. Finally, we show that $\varphi$ is an injection. If $\varphi(Ka)=\varphi(Kb)$, then $f(a)=f(b)$; hence $f(ab^{-1})=\mathbf 1,\ ab^{-1}\in K$, and $Ka=Kb$ (note that $\varphi$ being an injection is the converse of $\varphi$ being well defined). Thus we have shown that $\varphi$ is an isomorphism.
■

It follows that there is no significant difference between a quotient group and a homomorphic image.

If $\nu\!:G\rightarrow G/K$ is the natural map, then the following "commutative diagram" (i.e., $f=\varphi\circ\nu$) with surjection $\nu$ and injection $\varphi$ describes the theorem:

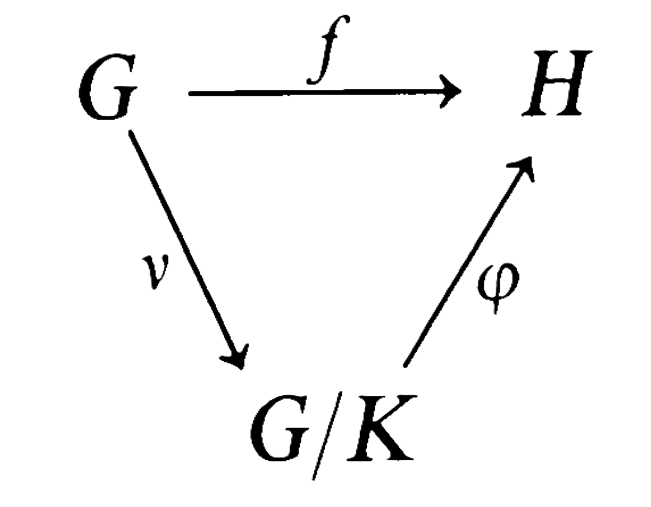
It is easy to describe $\varphi^{-1}\!:\mathrm{im}f\rightarrow G/K$: if $x\in\mathrm{im}f$, then there exists $a\in G$ with $f(a)=x$, and $\varphi^{-1}(x)=Ka$.

Proposition 2.6.2 A homomorphism $f\!:G\rightarrow H$ is an injection if and only if $\mathrm{ker}f=1$.

Lemma 2.6.3 If $S$ and $T$ are subgroups of $G$ and if one of them is normal, then $ST=S\lor T=TS$.

Proof

Recall that $ST$ and $TS$ are subsets of $S\lor T$ containing $S\cup T$. If $ST$ and $TS$ are subgroups, then the reverse inclusion will follow from Corollary 2.1.12. Assume that $T\lhd G$. If $s_1t_1$ and $s_2t_2\in ST$, then

$$\begin{aligned} (s_1t_1)(s_2t_2)^{-1}&=s_1t_1t_2^{-1}s_2^{-1}=s_1(s_2^{-1}s_2)t_1t_2^{-1}s_2^{-1}\\ &=s_1s_2^{-1}t_3=(s_1s_2^{-1})t_3\in ST, \end{aligned}$$

where $t_3=s_2(t_1t_2^{-1})s_2^{-1}\in T$ because $T\lhd G$. Therefore, $ST=S\lor T$. A similar proof shows that $TS$ is a subgroup, and so $TS=S\lor T=ST$.
■

Suppose that $S\le H\le G$ are subgroups with $S\lhd G$. Then $S\lhd H$ and the quotient $H/S$ is defined; it is the subgroup of $G/S$ consisting of all those cosets $Sh$ with $h\in H$. In particular, if $S\lhd G$ and $T$ is any subgroup of $G$, then $S\le ST\le G$ and $ST/S$ is the subgroup of $G/S$ consisting of all those cosets $Sst$, where $st\in ST$. Since $Sst=St$, it follows that $ST/S$ consists precisely of all those cosets of $S$ having a representative in $T$.

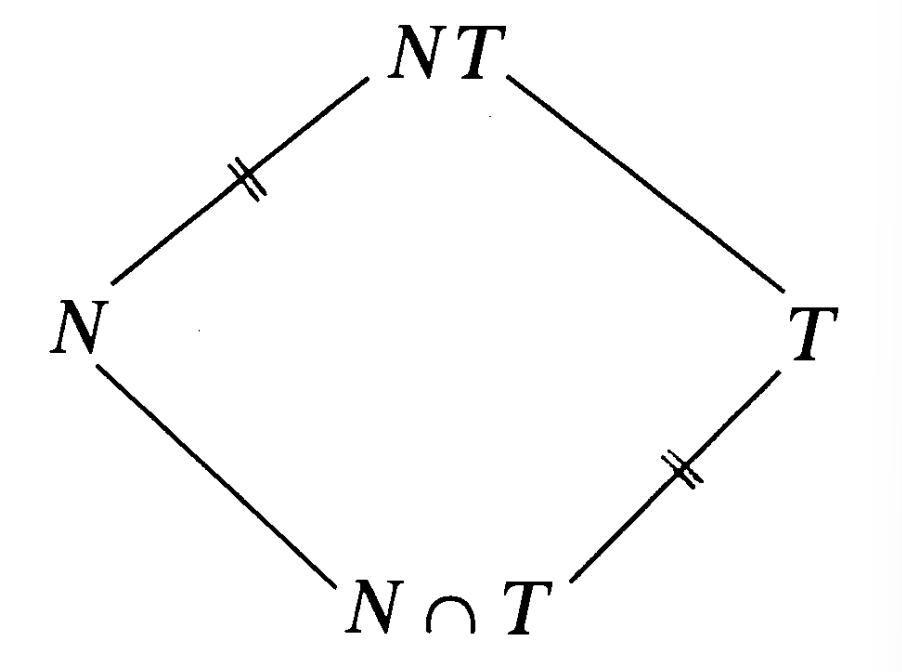
Theorem 2.6.4 (Second Isomorphism Theorem) Let $N$ and $T$ be subgroups of $G$ with $N$ normal. Then $N\cap T$ is normal in $T$ and $T/(N\cap T)\cong NT/N$.

Remark The following diagram is a mnemonic for this theorem:

Proof

Let $\nu\!:G\rightarrow G/N$ be the natural map, and let $\nu'=\nu\big|_T$, the restriction of $\nu$ to $T$. Since $\nu'$ is a homomorphism whose kernel is $N\cap T$, Theorem 2.6.1 gives $N\cap T\lhd T$ and $T/(N\cap T)\cong \mathrm{im}\nu'$. However, $\mathrm{im}\nu'$ is just the family of all those cosets of $N$ having a representative in $T$; that is, $\mathrm{im}\nu'$ consists of all the cosets in $NT/N$.
■

Theorem 2.6.5 (Third Isomorphism Theorem) Let $K\le H\le G$, where both $K$ and $H$ are normal subgroups of $G$. Then $H/K$ is a normal subgroup of $G/K$ and $(G/K)/(H/K)\cong G/H$.

Proof

Define $f\!:G/K\rightarrow G/H$ by $f(Ka)=Ha$ (this "enlargement of coset" map $f$ is well defined because $K\le H$). Then it is easily observed that $f$ is a surjective homomorphism with kernel $H/K$. By Theorem 2.6.1 we have $(G/K)/(H/K)\cong G/H$.
■

Proposition 2.6.6 (Modular Law) Let $A,B$ and $C$ be subgroups of $G$ with $A\le B$. If $A\cap C=B\cap C$ and $AC=BC$, then $A=B$.

Proposition 2.6.7 (Dedekind Law) Let $H,K$ and $L$ be subgroups of $G$ with $H\le L$. Then $HK\cap L=H(K\cap L)$.

Proposition 2.6.8 Let $f\!:G\rightarrow G^*$ be a homomorphism and let $S^*$ be a subgroup of $G^*$. Then $f^{-1}(S^*)=\{x\in G:f(x)\in S^*\}$ is a subgroup of $G$ containing $\mathrm{ker}f$.

Correspondence Theorem

Let $X$ and $X^*$ be sets. A function $f\!:X\rightarrow X^*$ induces a "forward motion" and a "backward motion" between subsets of $X$ and subsets of $X^*$. The forward motion assigns to each subset $S\subset X$ the subset $f(S)=\{f(s):s\in S\}$ of $X^*$; the backward motion assigns to each subset $S^*$ of $X^*$ the subset $f^{-1}(S^*)=\{x\in X:f(x)\in S^*\}$ of $X$. Morerover, if $f$ is a surjection, these motions define a bijection between all the subsets of $X^*$ and certain subsets of $X$.

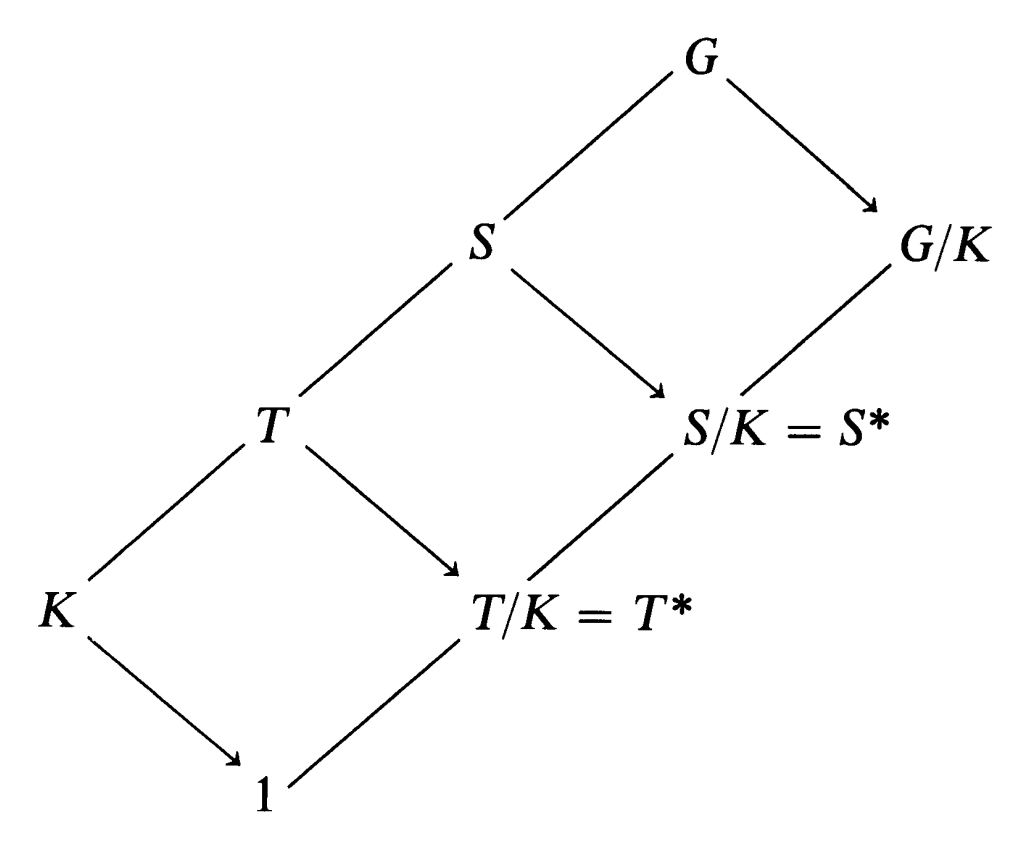
Theorem 2.7.1 (Correspondence Theorem) Let $K\lhd G$ and let $\nu\!:G\rightarrow G/K$ be the natural map. Then $S\mapsto \nu(S)=S/K$ is a bijection from the family of all those subgroups $S$ of $G$ which contain $K$ to the family of all the subgroups of $G/K$.

Moreover, if we denote $S/K$ by $S^*$, then:

1. $T\le S$ if and only if $T^*\le S^*$, and then $[S:T]=[S^*:T^*]$;
2. $T\lhd S$ if and only if $T^*\lhd S^*$, and then $S/T\cong S^*/T^*$.

Remark The following diagram is a mnemonic for this theorem:

Proof

We show first that $S\mapsto S/K$ is an injection: if $S$ and $T$ are subgroups containing $K$, and if $S/K=T/K$, then $S=T$. To see this, let $s\in S$; since $S/K=T/K$, there exists $t\in T$ with $Ks=Kt$. Hence, $s=kt$ for some $k\in K\le T$ and $s\in T$. The reverse inclusion is proved similarly. To see that the correspondence $S\mapsto S/K$ is a surjection, we must show that if $A\le G/K$, then there is a subgroup $S$ of $G$ containing $K$ with $A=S/K$. By Proposition 2.6.8 $S=\nu^{-1}(A)$ is a subgroup of $G$ containing $K$; moreover, that $\nu$ is a surjection implies that $S/K=\nu(S)=\nu\nu^{-1}(A)=A$.

It is plain that if $K\le T\le S$, then $T/K\le S/K$. To prove that $[S:T]=[S^*:T^*]$, it suffices to show that there is a bijection from the family of all cosets of the form $Ts$, where $s\in S$, to the family of all cosets $T^*s^*$, where $s^*\in S^*$. It is easy to check that $\alpha$, defined by $\alpha\!:Ts\mapsto T^*\nu(s)$, is such a bijection.

If $T\lhd S$, then the third isomorphism theorem gives $T/K\lhd S/K$ and $(S/K)/(T/K)\cong S/K$; that is, $T^*\lhd S^*$ and $S^*/T^*\cong S/T$. It remains to show that if $T^*\lhd S^*$, then $T\lhd S$. However, it is easily verified that $T=\mathrm{ker}\mu\nu_0\!:S\rightarrow S^*/T^*$, where $\nu_0=\nu\big|_S$ and $\mu\!:S^*\rightarrow S^*/T^*$ is the natural map.
■

Proposition 2.7.2 If $G'\le H\le G$, where $G'$ is the commutator subgroup of $G$, then $H\lhd G$ and $G/H$ is abelian.

Definition 2.7.3 A group $G\neq \mathbf 1$ is simple if it has no normal subgroups other than $G$ and $\mathbf 1$.

Proposition 2.7.4 A subgroup $H< G$ is a maximal subgroup of $G$ if there is no subgroup $N$ of $G$ with $H< N< G$. If $H\lhd G$ is a maximal subgroup, then $[G:H]$ is finite and equal to a prime.

Proposition 2.7.5 A subgroup $H< G$ is a maximal normal subgroup of $G$ if there is no normal subgroup $N$ of $G$ with $H< N< G$. Then $H$ is a maximal normal subgroup of $G$ if and only if $G/H$ is simple.

Proposition 2.7.6 (Schur) Let $f\!:G\rightarrow H$ be a homomorphism that does not send every element of $G$ into $\mathbf 1$. If $G$ is simple, then $f$ must be an injection.

Direct Products

Definition 2.8.1 If $H$ and $K$ are groups, then their direct product, denoted by $H\times K$, is the group with elements all ordered pairs $(h,k)$, where $h\in H$ and $k\in K$, and with operation

$$(h,k)(h',k')=(hh',kk').$$

It is easy to check that $H\times K$ is a group: the identity is $(\mathbf 1,\mathbf 1)$; the inverse $(h,k)^{-1}$ is $(h^{-1},k^{-1})$. Notice that neigher $H$ nor $K$ is a subgroup of $H\times K$, but $H\times K$ does contain isomorphic replicas of each, namely, $H\times \mathbf 1=\{(h,\mathbf 1):h\in H\}$ and $\mathbf 1\times K=\{(\mathbf 1,k):k\in K\}$.

Theorem 2.8.2 Let $G$ be a group with normal subgroups $H$ and $K$. If $HK=G$ and $H\cap K=\mathbf 1$, then $G\cong H\times K$.

Proof

If $a\in G$, then $a=hk$ for some $h\in H$ and $k\in K$ (because $G=HK$). We claim that $h$ and $k$ are uniquely determined by $a$. If $a=h_1k_1$ for $h_1\in H$ and $k_1\in K$, then $hk=h_1k_1$ and $h^{-1}h_1=kk_1^{-1}\in H\cap K=\mathbf 1$; hence $h=h_1$ and $k=k_1$.

Define $f\!:G\rightarrow H\times K$ by $f(a)=(h,k)$, where $a=hk$. If $a=hk$ and $a'=h'k'$, then $aa'=hkh'k'$ which is not in the proper form for evaluating $f$. However, we could consider the commutator $h'kh'^{-1}k^{-1}$. Now $(h'kh'^{-1})k^{-1}\in K$ for $K\lhd G$, and, similarly, $h'(kh'^{-1}k^{-1})\in H$; therefore, $h'kh'^{-1}k^{-1}\in H\cap K=\mathbf 1$ and $h'$ and $k$ commute. Now it is easily observed that $f$ is a homomorphism and a bijection; that is, $f$ is an isomorphism.
■

Theorem 2.8.3 If $A\lhd H$ and $B\lhd K$, then $A\times B\lhd H\times K$ and

$$(H\times K)/(A\times B)\cong (H/A)\times (K/B).$$

Proof

The homomorphism $\varphi\!:H\times K\rightarrow (H/A)\times (K/B)$, defined by $\varphi(h,k)=(Ah,Bk)$, is surjective and $\mathrm{ker}\varphi=A\times B$. The first isomorphism theorem now gives the result.
■

Corollary 2.8.4 If $G=H\times K$, then $G/(H\times \mathbf 1)\cong K$.

There are two versions of the direct product $H\times K$: the external version, whose elements are ordered pairs and which contains isomorphic copies of $H$ and $K$ (namely, $H\times \mathbf 1$ and $\mathbf 1\times K$); the internal version which does contain $H$ and $K$ as normal subgroups and in which $HK=G$ and $H\cap K=\mathbf 1$. By Theorem 2.8.2, the two versions are isomorphic. In the future, we shall not distinguish between external and internal; in almost all cases, however, our point of view is internal. For example, we shall write Corollary 2.8.4 as $(H\times K)/H\cong K$.

Proposition 2.8.5 The operation of direct product is commutative and associative in the following sense: for groups $H,K$ and $L$, we have

$$H\times K\cong K\times H\text{ and }H\times (K\times L)\cong (H\times K)\times L.$$

This means that the notations $H_1\times\cdots\times H_n$ and $\prod_{i=1}^nH_i$ are unambiguous.

Proposition 2.8.6 Let $G$ be a group having normal subgroups $H_1,\ldots,H_n$.

1. If $G=\left\langle\bigcup_{i=1}^nH_i\right\rangle$ and, for all $j$, $\mathbf 1=H_j\cap\left\langle\bigcup_{i\neq j}H_i\right\rangle$, then $G\cong H_1\times\cdots\times H_n$.
2. If each $a\in G$ has a unique expression of the form $a=h_1\ldots h_n$, where each $h_i\in H_i$, then $G\cong H_1\times\cdots\times H_n$.

Proposition 2.8.7 Let $H_1,\ldots,H_n$ be normal subgroups of a group $G$, and define $\varphi\!:G\rightarrow G/H_1\times\cdots\times G/H_n$ by $\varphi(x)=(H_1x,\ldots,H_nx)$, then we have

1. $\mathrm{ker}\varphi=H_1\cap\cdots\cap H_n$;
2. if each $H_i$ has finite index in $G$ and if $(|G/H_i|,|G/H_j|)=1$ for all $i\neq j$, then $\varphi$ is a surjection and

$$[G:H_1\cap\cdots\cap H_n]=\prod_{i=1}^n|G/H_i|.$$

Chapter III. Symmetric Groups and $G$-Sets

Conjugates

Lemma 3.1.1 If $G$ is a group, then the relation "$y$ is a conjugate of $x$ in $G$," that is, $y=gxg^{-1}$ for some $g\in G$, is an equivalence relation.

Definition 3.1.2 If $G$ is a group, then the equivalence class of $a\in G$ under the relation "$y$ is a conjugate of $x$ in $G$" is called the conjugacy class of $a$; it is denoted by $a^G$.

If $a$ and $b$ are conjugate in $G$, say, $b=gag^{-1}$, then there is an isomorphism $\gamma_g\!:G\rightarrow G$, namely, conjugation by $g$, with $\gamma_g(a)=b$. It follows that all the elements in the same conjugacy class have the same order.

If $a\in G$ is the sole resident of its conjugacy class, then $a=gag^{-1}$ for all $g\in G$; that is, $a$ commutes with every element of $G$.

Definition 3.1.3 The center of a group $G$, denoted by $\mathrm Z(G)$, is the set of all $a\in G$ that commute with every element of $G$.

It is easy to check that $\mathrm Z(G)$ is a normal abelian subgroup of $G$.

Definition 3.1.4 If $a\in G$, then the centralizer of $a$ in $G$, denoted by $\mathrm C_G(a)$, is the set of all $x\in G$ which commute with $a$.

It is easy to check that $\mathrm C_G(a)$ is a subgroup of $G$.

Theorem 3.1.5 If $a\in G$, the number of conjugates of $a$ is equal to the index of its centralizer:

$$\left|a^{G}\right|=[G:\mathrm C_G(a)],$$

and this number is a divisor of $|G|$ when $G$ is finite.

Proof

Denote the family of all left cosets of $C=\mathrm C_G(a)$ in $G$ by $G/C$, and define $f\!:a^G\rightarrow G/C$ by $f(gag^{-1})=gC$. Now $f$ is well defined: if $gag^{-1}=hah^{-1}$ for some $h\in G$, then $h^{-1}gag^{-1}h=a$ and $h^{-1}g$ commutes with $a$; that is, $h^{-1}g\in C$, and so $hC=gC$. The function $f$ is an injection: if $gC=f(gag^{-1})=f(kak^{-1})=kC$ for some $k\in G$, then $k^{-1}g\in C$, $k^{-1}g$ commutes with $a$, $k^{-1}gag^{-1}k=a$, and $gag^{-1}=kak^{-1}$; the function $f$ is a surjection: if $g\in G$, then $gC=f(gag^{-1})$. Therefore, $f$ is a bijection and $\left|a^G\right|=|G/C|=[G:\mathrm C_G(a)]$. When $G$ is finite, Lagrange's theorem applies.
■

Definition 3.1.6 If $H\le G$ and $g\in G$, then the conjugate $gHg^{-1}$ is $\{ghg^{-1}:h\in H\}$. The conjugate $gHg^{-1}$ is often denoted by $H^g$.

The conjugate $H^g$ is a subgroup of $G$ isomorphic to $H$: if $\gamma_g\!:G\rightarrow G$ is conjugation by $g$, then $\gamma_g\big|_H$ is an isomorphism from $H$ to $H^g$.

Note that a subgroup $H$ is a normal subgroup if and only if it has only one conjugate.

Definition 3.1.7 If $H\le G$, then the normalizer of $H$ in $G$, denoted by $\mathrm N_G(H)$, is

$$\mathrm N_G(H)=\{a\in G:aHa^{-1}=H\}.$$

It is immediate that $\mathrm N_G(H)$ is a subgroup of $G$. Notice that $H\lhd\mathrm N_G(H)$; indeed, $\mathrm N_G(H)$ is the largest subgroup of $G$ in which $H$ is normal.

Theorem 3.1.8 If $H\le G$, then the number $c$ of conjugates of $H$ in $G$ is equal to the index of its normalizer: $c=[G:\mathrm N_G(H)]$, and $c$ divides $|G|$ when $G$ is finite. Moreover, $H^a=H^b$ if and only if $b^{-1}a\in \mathrm N_G(H)$.

Proof

Let $[H]$ denote the family of all the conjugates of $H$, and let $G/N$ denote the family of all left cosets of $N=\mathrm N_G(H)$ in $G$. Define $f\!:[H]\rightarrow G/N$ by $f(H^a)=aN$. Now $f$ is well defined: if $H^a=H^b$ for some $b\in G$, then $H^{b^{-1}a}=H$ and $b^{-1}a$ normalizes $H$; that is, $b^{-1}a\in N$, and so $bN=aN$. The function $f$ is an injection: if $aN=f(H^a)=f(H^c)=cN$ for some $c\in G$, then $c^{-1}a\in N$, $c^{-1}a$ normalizes $H$, $H^{c^{-1}a}=H$, and $H^a=H^c$; the function $f$ is a surjection: if $a\in G$, then $aN=f(H^a)$. Therefore, $f$ is a bijection and $|[H]|=|G/N|=[G:\mathrm N_G(H)]$. When $G$ is finite, Lagrange's theorem applies.
■

Proposition 3.1.9 Let $H$ be a subgroup of $G$, and $a\in G$, then we have

1. $\mathrm N_G(H^{a})=\mathrm N_G(H)^{a}$; that is, $\mathrm N_G(aHa^{-1})=a\mathrm N_G(H)a^{-1}$;
2. If $H\le K\le G$, then $\mathrm N_K(H)=\mathrm N_G(H)\cap K$.
3. If $H,K\le G$, then $\mathrm N_G(H)\cap \mathrm N_G(K)\le \mathrm N_G(H\cap K)$.

Definition 3.1.10 If $H$ is a subset of $G$, then the centralizer of $H$ in $G$, denoted by $\mathrm C_G(H)$, is the set of all $x\in G$ which commute with any element in $H$; that is, $\mathrm C_G(H)=\{x\in G:xy=yx\text{ for every }y\in H\}$.

Proposition 3.1.11 Let $H$ be a subset of $G$, then we have

1. $\mathrm C_G(H)$ is a subgroup of $G$; that is, $\mathrm C_G(H)\le G$;
2. $\mathrm C_G(H)\lhd \mathrm N_G(H)$ when $H\le G$.

Proposition 3.1.12 If $H\le G$, then $\mathrm N_G(H)\le\{a\in G:aHa^{-1}\le H\}$.

Remark When $H\le G$ is an infinite subgroup, there may exist $a\in G$ such that $H^a=aHa^{-1}< H$.

Proposition 3.1.13 If $H$ is a proper subgroup of a finite group $G$, then $G$ is not the union of all the conjugates of $H$.

Proposition 3.1.14 If $G$ is a finite group with conjugacy classes $C_1,\ldots,C_m$, and if $g_i\in C_i$, then $G=\langle g_1,\ldots,g_m\rangle$.

Proposition 3.1.15 Let $G$ be a finite group, let $H$ be a normal subgroup of prime index, and let $x\in H$ satisfy $\mathrm C_H(x)<\mathrm C_G(x)$. If $y\in H$ is conjugate to $x$ in $G$, then $y$ is conjugate to $x$ in $H$.

Definition 3.1.16 Let $G$ be a group. If $\mathrm Z(G)=\mathbf 1$, we call $G$ centerless.

Proposition 3.1.17 If $n\ge 3$, then $\mathrm S_n$ is centerless.

Proposition 3.1.18 If $\alpha\in \mathrm S_n$ is an $n$-cycle, then its centralizer is $\langle \alpha\rangle$.

Proposition 3.1.19

1. Let $G$ be a group. If $G$ is not abelian, then $G/\mathrm Z(G)$ is not cyclic.
2. If $G$ is a group with $G=G'$, then $G/\mathrm Z(G)$ is centerless.
3. If $H\lhd G$ and $H\cap G'=\mathbf 1$, then $H\le \mathrm Z(G)$.

Symmetric Group

Definition 3.2.1 Two permutations $\alpha,\beta\in\mathrm S_n$ have the same cycle structure if their complete factorizations into disjoint cycles have the same number of $r$-cycles for each $r$.

Lemma 3.2.2 If $\alpha,\beta\in \mathrm S_n$, then $\alpha\beta\alpha^{-1}$ is the permutation with the same cycle structure as $\beta$ which is obtained by applying $\alpha$ to the symbols in $\beta$.

Proof

Let $\pi$ be the permutation defined in the lemma. If $\beta$ fixes a symbol $i$, then $\pi$ fixes $\alpha(i)$, for $\alpha(i)$ resides in a $1$-cycle; but $\alpha\beta\alpha^{-1}(\alpha(i))=\alpha\beta(i)=\alpha(i)$, and so $\alpha\beta\alpha^{-1}$ fixes $\alpha(i)$ as well. Assume that $\beta$ moves $i$; say, $\beta(i)=j$. Let the complete factorization of $\beta$ be

$$\beta=\gamma_1\gamma_2\cdots(\cdots\ \ i\ \ j\ \ \cdots)\cdots\gamma_t.$$

If $\alpha(i)=k$ and $\alpha(j)=l$, then $\pi\!:k\mapsto l$. But $\alpha\beta\alpha^{-1}\!:k\mapsto i\mapsto j\mapsto l$, and so $\alpha\beta\alpha^{-1}=\pi(k)$. Therefore, $\pi$ and $\alpha\beta\alpha^{-1}$ agree on all symbols of the form $k=\alpha(i)$; since $\alpha$ is a surjection, it follows that $\pi=\alpha\beta\alpha^{-1}$.
■

Theorem 3.2.3 Permutations $\alpha,\beta\in\mathrm S_n$ are conjugate if and only if they have the same cycle structure.

Proof

The lemma shows that conjugate permutations do have the same cycle structure. For the converse, define $\gamma\in \mathrm S_n$ as follows: place the complete factorization of $\alpha$ over that of $\beta$ so that cycles of the same length correspond, and let $\gamma$ be the function sending the top to the bottom. For example, if

$$\begin{aligned} \alpha&=\gamma_1\gamma_2\cdots(\cdots\ \ i\ \ j\ \ \cdots)\cdots\gamma_t,\\ \beta&=\delta_1\delta_2\cdots(\cdots\ \ k\ \ l\ \ \cdots)\cdots\delta_t, \end{aligned}$$

then $\gamma(i)=k,\gamma(j)=l$, etc. Notice that $\gamma$ is a permutation, for every $i$ between $1$ and $n$ occurs exactly once in a complete factorization. The lemma gives $\gamma\alpha\gamma^{-1}=\beta$, and so $\alpha$ and $\beta$ are conjugate.
■

Corollary 3.2.4 A subgroup $H$ of $\mathrm S_n$ is a normal subgroup if and only if, whenever $\alpha\in H$, then every $\beta$ having the same cycle structure as $\alpha$ also lies in $H$.

Definition 3.2.5 If $n$ is a positive integer, then a partition of $n$ is a sequence of integers $1\le i_1\le i_2\le \cdots\le i_r$ with $\sum{i_j}=n$.

Proposition 3.2.6 The number of conjugacy classes in $\mathrm S_n$ is the number of partitions of $n$.

The Simplicity of Alternating Groups

Lemma 3.3.1 $\mathrm A_5$ is simple.

Proof

(i). All $3$-cycles are conjugate in $\mathrm A_5$.
If, for example, $\alpha=(1\ \ 2\ \ 3)$, then the odd permutation $(4\ \ 5)$ commutes with $\alpha$. Since $\mathrm A_5$ has index $2$ in $\mathrm S_5$, it is a normal subgroup of prime index, and so Proposition 3.1.15 says that $\alpha$ has the same number of conjugates in $\mathrm A_5$ as it does in $\mathrm S_5$ because $\mathrm C_{\mathrm A_5}(\alpha)< \mathrm C_{\mathrm S_5}(\alpha)$.

(ii). All products of distinct transpositions are conjugate in $\mathrm A_5$.
If, for example, $\alpha=(1\ \ 2)(3\ \ 4)$, then the odd permutation $(1\ \ 2)$ commutes with $\alpha$. Since $\mathrm A_5$ has index $2$ in $\mathrm S_5$, Proposition 3.1.15 says that $\alpha$ has the same number of conjugates in $\mathrm A_5$ as it does in $\mathrm S_5$.

(iii). There are two conjugacy classes of $5$-cycles in $\mathrm A_5$, each of which has $12$ elements.
In $\mathrm S_5$, $\alpha=(1\ \ 2\ \ 3\ \ 4\ \ 5)$ has $24$ conjugates, so that $\mathrm C_{\mathrm S_5}(\alpha)$ has $5$ elements; these must be the powers of $\alpha$. By Proposition 3.1.18, $\mathrm C_{\mathrm A_5}(\alpha)$ has order $5$, hence, index $60/5=12$.

We have now surveyed all the conjugacy classes occuring in $\mathrm A_5$. Since every normal subgroup $H$ is a union of conjugacy classes, $|H|$ is a sum of $1$ and certain of the numbers: $12$, $12$, $15$, and $20$. It is easily checked that no such sum is a proper divisor of $60$, so that $|H|=60$ and $\mathrm A_5$ is simple.
■

Lemma 3.3.2 Let $H\lhd \mathrm A_n$, where $n\ge 5$. If $H$ contains a $3$-cycle, then $H=\mathrm A_n$.

Proof

We show that $(1\ \ 2\ \ 3)$ and $(i\ \ j\ \ k)$ are conjugate in $\mathrm A_n$ (and thus that all $3$-cycles are conjugate in $\mathrm A_n$). If these cycles are not disjoint, then each fixes all the symbols outside of $\{1,2,3,i,j\}$, say, and the two $3$-cycles lie in $A^*$, the group of all even permutations on these $5$ symbols. Of course, $A^*\cong \mathrm A_5$, and, as in part (i) of the previous proof, $(1\ \ 2\ \ 3)$ and $(i\ \ j\ \ k)$ are conjugate in $A^*$; a fortiori, they are conjugate in $\mathrm A_n$. If the cycles are disjoint, then we have just seen that $(1\ \ 2\ \ 3)$ is conjugate to $(3\ \ j\ \ k)$ and that $(3\ \ j\ \ k)$ is conjugate to $(i\ \ j\ \ k)$, so that $(1\ \ 2\ \ 3)$ is conjugate to $(i\ \ j\ \ k)$ in this case as well.

A normal subgroup $H$ containing a $3$-cycle $\alpha$ must contain every conjugate of $\alpha$; as all $3$-cycles are conjugate, $H$ contains every $3$-cycle. But Proposition 2.1.20 shows that $\mathrm A_n$ is generated by the $3$-cycles, and so $H=\mathrm A_n$.
■

Lemma 3.3.3 $\mathrm A_6$ is simple.

Proof

Let $H\neq \mathbf 1$ be a normal subgroup of $\mathrm A_6$, and let $\alpha\in H$ be distinct from $\mathbf 1$. If $\alpha$ fixes some $i$, define

$$F=\{\beta\in\mathrm A_6:\beta(i)=i\}.$$

Now $F\cong \mathrm A_5$ and $\alpha\in H\cap F$. But $H\cap F\lhd F$, by the second isomorphism theorem, so that $F$ simple and $H\cap F\neq \mathbf 1$ give $H\cap F=F$; that is, $F\le H$. Therefore, $H$ contains a $3$-cycle, $H=\mathrm A_6$ (by the lemma), and we are done.

We may now assume that no $\alpha\in H$ with $\alpha\neq\mathbf 1$ fixes any $i$, for $1\le i\le 6$. It could be easily shown that the cycle structure of $\alpha$ is either $(1\ \ 2)(3\ \ 4\ \ 5\ \ 6)$ or $(1\ \ 2\ \ 3)(4\ \ 5\ \ 6)$. In the first case, $\alpha^2\in H,\,\alpha^2\neq\mathbf 1$, and $\alpha^2$ fixes $1$ (and $2$), a contradiction. In the second case, $H$ contains $\alpha(\beta\alpha^{-1}\beta^{-1})$, where $\beta=(2\ \ 3\ \ 4)$, and it is easily checked that this element is not the identity and it fixes $1$, a contradiction. Therefore, no such normal subgroup $H$ can exist.
■

Theorem 3.3.4 $\mathrm A_n$ is simple for all $n\ge 5$.

Proof

Let $n\ge 5$ and let $H\neq 1$ be a normal subgroup of $\mathrm A_n$. If $\beta\in H$ and $\beta \neq \mathbf 1$, then there is an $i$ with $\beta(i)=j\neq i$. If $\alpha$ is a $3$-cycle fixing $i$ and moving $j$, then $\alpha$ and $\beta$ do not commute: $\beta\alpha(i)=\beta(i)=j$ and $\alpha\beta(i)\alpha(j)\neq j$; therefore, their commutator is not the identity. Furthermore, $\alpha(\beta\alpha^{-1}\beta^{-1})$ lies in the normal subgroup $H$, and, by Lemma 3.2.2, it is a product of two $3$-cycles $(\alpha\beta\alpha^{-1})\beta^{-1}$; thus it moves at most $6$ symbols, say, $i_1,\ldots,i_6$. If $F=\{\gamma\in\mathrm A_m:\gamma\text{ fixes the other symbols}\}$, then $F\cong \mathrm A_6$ and $\alpha\beta\alpha^{-1}\beta^{-1}\in H\cap F\lhd F$. Since $\mathrm A_6$ is simple, $H\cap F=F$ and $F\le H$. Therefore $H$ contains a $3$-cycle, $H=\mathrm A_n$ (Lemma 3.3.2), and the proof is complete.
■

Proposition 3.3.5 If $n\neq 4$, then $\mathrm A_n$ is the only proper nontrivial normal subgroup of $\mathrm S_n$.

Proposition 3.3.6 If $X=\{1,2,\ldots\}$ is the set of all positive integers, then the infinite alternating group $\mathrm A_{\infty}$ is the subgroup of $\mathrm S_X$ generated by all the $3$-cycles, and we have that $\mathrm A_{\infty}$ is an infinite simple group.

Some Representation Theorems

Theorem 3.4.1 (Cayley) Every group $G$ can be imbedded as a subgroup of $\mathrm S_G$. In particular, if $|G|=n$, then $G$ can be imbedded in $\mathrm S_n$.

Proof

Recall that for each $a\in G$, left translation $L_a\!:G\rightarrow G$, defined by $x\mapsto ax$, is a bijection; that is, $L_a\in\mathrm S_G$. The theorem is proved if the function $L\!:G\rightarrow \mathrm S_G$, given by $a\mapsto L_a$ is an injection and a homomorphism, for then $G\cong \mathrm{im}L$. If $a\neq b$, then $L_a(\mathbf 1)=a\neq b=L_b(\mathbf 1)$, and so $L_a\neq L_b$. Finally, we show that $L_{ab}=L_a\circ L_b$. If $x\in G$, then $L_{ab}(x)=(ab)x$, while $(L_a\circ L_b)(x)=L_a(L_b(x))=L_a(bx)=a(bx)$; associativity shows that these are the same.
■

Definition 3.4.2 The homomorphism $L\!:G\rightarrow \mathrm S_G$, given by $a\mapsto L_a$, is called the left regular representation of $G$.

Corollary 3.4.3 If $k$ is a field and $G$ is a finite group of order $n$, then $G$ can be imbedded in $\mathrm {GL}(n,k)$.

Proof

The group $P(n,k)$ of all $n\times n$ permutation matrices is a subgroup of $\mathrm {GL}(n,k)$ that is isomorphic to $\mathrm S_n$. Now apply Cayley's theorem to imbed $G$ into $P(n,k)$.
■

Theorem 3.4.4 If $H\le G$ and $[G:H]=n$, then there is a homomorphism $\rho\!:G\rightarrow \mathrm S_n$ with $\mathrm{ker}\rho\le H$.

Proof

If $a\in G$ and $X$ is the family of all the left cosets of $H$ in $G$, define a function $\rho_a\!:X\rightarrow X$ by $gH\mapsto agH$ for all $g\in G$. It is easy to check that each $\rho_a$ is a permutation of $X$ (its inverse is $\rho_{a^{-1}}$) and that $a\mapsto \rho_a$ is a homomorphism $\rho\!:G\rightarrow \mathrm S_X\cong \mathrm S_n$. If $a\in\mathrm{ker}\rho$, then $agH=gH$ for all $g\in G$; in particular, $aH=H$, and so $a\in H$; therefore, $\mathrm{ker}\rho\le H$.
■

Definition 3.4.5 The homomorphism $\rho$ in Theorem 3.4.4 is called the representation of $G$ on the cosets of $H$.

Corollary 3.4.6 A simple group $G$ which contains a subgroup $H$ of index $n$ can be imbedded in $\mathrm S_n$.

Proof

There is a homomorphism $\rho\!:G\rightarrow \mathrm S_n$ with $\mathrm {ker}\rho\le H< G$. Since $G$ is simple, $\mathrm{ker}\rho=\mathbf 1$, and so $\rho$ is an injection.
■

Theorem 3.4.7 Let $H\le G$ and let $X$ be the family of all the conjugates of $H$ in $G$. There is a homomorphism $\psi\!:G\rightarrow \mathrm S_X$ with $\mathrm{ker}\psi\le \mathrm N_G(H)$.

Proof

If $a\in G$, define $\psi_a\!:X\rightarrow X$ by $\psi_a(gHg^{-1})=agHg^{-1}a^{-1}$. If $b\in G$, then

$$\psi_a\psi_b(gHg^{-1})=\psi_a(bgHg^{-1}b^{-1})=abgHg^{-1}b^{-1}a^{-1}=\psi_{ab}(gHg^{-1}).$$

We conclude that $\psi_a$ has inverse $\psi_{a^{-1}}$, so that $\psi_a\in\mathrm S_X$ and $\psi\!:G\rightarrow \mathrm S_X$ is a homomorphism.

If $a\in\mathrm{ker}\psi$, then $agHg^{-1}a^{-1}=gHg^{-1}$ for all $g\in G$. In particular, $aHa^{-1}=H$, and so $a\in \mathrm N_G(H)$; hence $\mathrm{ker}\psi\le\mathrm N_G(H)$.
■

Definition 3.4.8 The homomorphism $\psi$ in Theorem 3.4.7 is called the representation of $G$ on the conjugates of $H$.

Proposition 3.4.9 If $\rho$ is the representation of a group $G$ on the cosets of a subgroup $H$, then $\mathrm{ker}\rho=\bigcap_{x\in G}H^x$.

Proposition 3.4.10 If $\psi$ is the representation of a group $G$ on the conjugates of a subgroup $H$, then $\mathrm{ker}\psi=\bigcap_{x\in G}\mathrm N_G(H)^x$.

Proposition 3.4.11 Let $a\in G$, where $G$ is finite. If $a^n$ has $m$ conjugates and $a$ has $k$ conjugates, then $m|k$.

Proposition 3.4.12 If $H$ and $K$ are subgroups of $G$ having finite index, then $[G:H\cap K]\le [G:H][G:K]$. Moreover, if $([G:H],[G:K])=1$, then $[G:H\cap K]=[G:H][G:K]$.

Proposition 3.4.13 Let $G$ be an infinite simple group, then

1. every $x\in G$ with $x\neq \mathbf 1$ has infinitely many conjugates;
2. every proper subgroup $H\neq \mathbf 1$ has infinitely many conjugates.

Proposition 3.4.14 If $A$ and $G$ are groups, then a homomorphism $h\!:A\rightarrow G$ is a surjection if and only if it is right cancellable: for every group $L$ and every pair of homomorphisms $f,g\!:G\rightarrow L$, the equation $f\circ h=g\circ h$ implies $f=g$.

Proposition 3.4.15 Let $G$ be a finite group containing a subgroup $H$ of index $p$, where $p$ is the smallest prime divisor of $|G|$. Then $H$ is a normal subgroup of $G$.

$G$-Sets

Definition 3.5.1 If $X$ is a set and $G$ is a group, then $X$ is a $G$-set if there is a function $\alpha\!:G\times X\rightarrow X$ (called an action), denoted by $\alpha\!:(g,x)\mapsto gx$, such that:

1. $\mathbf 1x=x$ for all $x\in X$;
2. $g(hx)=(gh)x$ for all $g,h\in G$ and $x\in X$.

One also says that $G$ acts on $X$. If $|X|=n$, then $n$ is called the degree of the $G$-set $X$.

Theorem 3.5.2 If $X$ is a $G$-set with action $\alpha$, then there is a homomorphism $\tilde\alpha\!:G\rightarrow \mathrm S_X$ given by $\tilde\alpha(g)\!:x\mapsto gx=\alpha(g,x)$. Conversely, every homomorphism $\varphi\!:G\rightarrow\mathrm S_X$ defines an action, namely, $gx=\varphi(g)x$, which makes $X$ into a $G$-set.

Proof

If $X$ is a $G$-set, $g\in G$, and $x\in X$, then

$$\tilde\alpha(g^{-1})\tilde\alpha(g)\!:x\mapsto \tilde\alpha(g^{-1})(gx)=g^{-1}(gx)=(g^{-1}g)x=\mathbf 1x=x;$$

it follows that each $\tilde\alpha(g)$ is a permutation of $X$ with the inverse $\tilde\alpha(g^{-1})$. That $\tilde\alpha$ is a homomorphism is immediate from (ii) of the definition of $G$-set. The converse is also routine.
■

If $\sigma\in\mathrm S_n$, define

$$g^{\sigma}(x_1,\ldots,x_n)=g(x_{\sigma 1},\ldots,x_{\sigma n});$$

If $g^{\sigma}=g$ for all $\sigma\in\mathrm S_n$, then $g$ is called a symmetric function. If a polynomial $f(x)=\sum_{i=0}^na_ix^i$ has roots $r_1,\ldots,r_n$, then each of the coefficients $a_i$ of $f(x)=a_n\prod_{i=0}^n(x-r_i)$ is a symmetric function of $r_1,\ldots,r_n$. Other interesting functions of the roots may not be symmetric. For example, the discriminant of $f(x)$ is defined to be the numer $d^2$, where $d=\prod_{i< j}(r_i-r_j)$. If $D(x_1,\ldots,x_n)=\prod_{i< j}(x_i-x_j)$, then it is easy to see, for every $\sigma\in\mathrm S_n$, that $D^{\sigma}=\pm D$. Indeed, $D$ is an alternating function of the roots: $D^{\sigma}=D$ if and only if $\sigma\in\mathrm A_n$.

Given $g(x_1,\ldots,x_n)$, find

$$\mathscr S(g)=\{\sigma\in\mathrm S_n:g^{\sigma}=g\};$$

it is easy to see that $\mathscr S(g)\le \mathrm S_n$; moreover, $g$ is symmetric if and only if $\mathscr S(g)=\mathrm S_n$, while $\mathscr S(D)=\mathrm A_n$.

Definition 3.5.3 If $X$ is a $G$-set and $x\in X$, then the $G$-orbit of $x$ is

$$Gx=\mathcal O(x)=\{gx:g\in G\}\subset X$$

Usually, we will say orbit instead of $G$-orbit. The orbits of $X$ form a partition; indeed, the relation $x\equiv y$ defined by "$y=gx$ for some $g\in G$" is an equivalence relation whose equivalence classes are the orbits.

Definition 3.5.4 If $X$ is a $G$-set and $x\in X$, then the stabilizer of $x$, denoted by $G_x$, is the subgroup

$$G_x=\{g\in G:gx=x\}\le G.$$

Example 3.5.5 If $G$ acts on itself by conjugation and $x\in G$, then $\mathcal O(x)$ is the conjugacy class of $x$ and $G_x=\mathrm C_G(x)$.

Example 3.5.6 If $G$ acts by conjugation on the family of all its subgroups and if $H\le G$, then $\mathcal O(H)=\{\text{all the conjugates of }H\}$ and $G_H=\mathrm N_G(H)$.

Theorem 3.5.7 If $X$ is a $G$-set and $x\in X$, then

$$|\mathcal O(x)|=[G:G_x].$$

Proof

If $x\in X$, let $G/G_x$ denote the family of all left cosets of $G_x$ in $G$. Define $f\!:\mathcal O(x)\rightarrow G/G_x$ by $f(ax)=aG_x$. Now $f$ is well defined: if $ax=bx$ for some $b\in G$, then $b^{-1}ax=x$, $b^{-1}a\in G_x$, and $aG_x=bG_x$. The function $f$ is an injection: if $aG_x=f(ax)=f(cx)=cG_x$ for some $c\in G$, then $c^{-1}a\in G_x$, $c^{-1}ax=x$, and $ax=cx$; the function $f$ is a surjection: if $a\in G$, then $aG_x=f(ax)$. Therefore, $f$ is a bijection and $|\mathcal O(x)|=|G/G_x|=[G:G_x]$.
■

Corollary 3.5.8 If a finite group $G$ acts on a set $X$, then the number of elements in any orbit is a divisor of $|G|$.

Proposition 3.5.9 Let $X$ be a $G$-set, let $x,y\in X$, and let $y=gx$ for some $g\in G$. Then we have $G_y=gG_xg^{-1}$, and also $|G_y|=|G_x|$.

Definition 3.5.10 A $G$-set $X$ is transitive if it has only one orbit; that is, for every $x,y\in X$, there exists $\sigma\in G$ with $y=\sigma x$.

Proposition 3.5.11 If $X$ is a $G$-set, then each of its orbits is a transitive $G$-set.

Proposition 3.5.12 If $H\le G$, then $G$ acts transitively on the set of all left cosets of $H$, and $G$ acts transitively on the set of all conjugates of $H$.

Proposition 3.5.13 Let $X$ be a $G$-set with action $\alpha\!:G\times X\rightarrow X$, and let $\tilde\alpha\!:G\rightarrow \mathrm S_X$ send $g\in G$ into the permutation $x\mapsto gx$.

1. If $K=\mathrm{ker}\tilde\alpha$, then $X$ is a $(G/K)$-set if one defines $(gK)x=gx$.
2. If $X$ is a transitive $G$-set, then $X$ is a transitive $(G/K)$-set.
3. If $X$ is a transitive $G$-set, then $|\mathrm{ker}\tilde\alpha|\le |G|/|X|$.

Proposition 3.5.14 If $G\le \mathrm S_n$, then $G$ acts on $X=\{1,2,\ldots,n\}$. In particular, $\langle\alpha\rangle$ acts on $X$ for every $\alpha\in\mathrm S_n$. If the complete factorization of $\alpha$ into disjoint cycles is $\alpha=\beta_1\ldots\beta_t$ and if $i$ is a symbol appearing in $\beta_j$, then $\mathcal O(i)=\{\alpha^{k}(i):k\in\mathbb Z\}$ consists of all the symbols appearing in $\beta_j$.

Counting Orbits

Let us call a $G$-set $X$ finite if both $X$ and $G$ are finite.

Theorem 3.6.1 (Burnside's Lemma) If $X$ is a finite $G$-set and $N$ is the number of $G$-orbits of $X$, then

$$N=(1/|G|)\sum_{\tau\in G}F(\tau),$$

where, for $\tau\in G$, $F(\tau)$ is the number of $x\in X$ fixed by $\tau$.

Proof

In the sum $\sum_{\tau\in G}F(\tau)$, each $x\in X$ is counted $|G_x|$ times (for $G_x$ consists of all those $\tau\in G$ which fix $x$). If $x$ and $y$ lie in the same orbit, then Proposition 3.5.9 gives $|G_y|=|G_x|$, and so the $[G:G_x]$ elements constituting the orbit of $x$ are, in the above sum, collectively counted $[G:G_x]|G_x|=|G|$ times. Each orbit thus contributes $|G|$ to the sum, and so $\sum_{\tau\in G}F(\tau)=N|G|$.
■

Corollary 3.6.2 If $X$ is a finite transitive $G$-set with $|X|>1$, then there exists $\tau\in G$ having no fixed points.

Proof

Since $X$ is transitive, the number $N$ of orbits of $X$ is $1$, and so Burnside's lemma gives

$$1=(1/|G|)\sum_{\tau\in G}F(\tau).$$

Now $F(\mathbf 1)=|X|>1$; if $F(\tau)>0$ for every $\tau\in G$, then the right hand side is too large.
■

Definition 3.6.3 If $G\le \mathrm S_X$, where $X=\{1,\ldots,n\}$, and if $\mathscr C$ is a set of colors, then $\mathscr C^n$ is a $G$-set if we define $\tau(c_1,\ldots,c_n)=(c_{\tau 1},\ldots,c_{\tau n})$ for all $\tau\in G$. If $|\mathscr C|=q$, then an orbit of $\mathscr C^n$ is called a $(q,G)$-coloring of $X$.

Lemma 3.6.4 Let $\mathscr C$ be a set of $q$ colors, and let $G\le \mathrm S_X\cong \mathrm S_n$. If $\tau\in G$, then $F(\tau)=q^{t(\tau)}$, where $t(\tau)$ is the number of cycles occurring in the complete factorization of $\tau$.

Proof

Since $\tau(c_1,\ldots,c_n)=(c_{\tau 1},\ldots,c_{\tau n})=(c_1,\ldots,c_n)$, we see that $c_{\tau i}=c_i$ for all $i$, and so $\tau i$ has the same color as $i$. It follows that $\tau^ki$ has the same color as $i$, for all $k$; that is, all $i$ in the $\langle\tau\rangle$-orbit of $X$ have the same color. But Proposition 3.5.14 shows that if the complete factorization of $\tau$ is $\tau=\beta_1\ldots\beta_{t(\tau)}$, and if $i$ occurs in $\beta_j$, then the set of symbols occuring in $\beta_j$ is the $\langle\tau\rangle$-orbit containing $i$. Since there are $t(\tau)$ orbits and $q$ colors, there are $q^{t(\tau)}$ $n$-tuples fixed by $\tau$ in its action on $\mathscr C^n$.
■

Definition 3.6.5 If the complete factorization of $\tau\in\mathrm S_n$ has $e_r(\tau)\ge 0$ $r$-cycles, then the index of $\tau$ is

$$\mathrm{ind}(\tau)=x_1^{e_1(\tau)}x_2^{e_2(\tau)}\ldots x_n^{e_n(\tau)}.$$

If $G\le \mathrm S_n$, then the cycle index of $G$ is the polynomial

$$P_G(x_1,\ldots,x_n)=(1/|G|)\sum_{\tau\in G}\mathrm{ind}(\tau)\in \mathbb Q[x_1,\ldots,x_n].$$

Corollary 3.6.6 If $|X|=n$ and $G\le \mathrm S_n$, then the number of $(q,G)$-colorings of $X$ is $P_G(q,\ldots,q)$.

Proof

By Burnside's lemma for the $G$-set $\mathscr C^n$, the number of $(q,G)$-colorings of $X$ is

$$(1/|G|)\sum_{\tau\in G}F(\tau).$$

By Lemma 3.6.4, this number is

$$(1/|G|)\sum_{\tau\in G}q^{t(\tau)},$$

where $t(\tau)$ is the number of cycles in the complete factorization of $\tau$. On the other hand,

$$\begin{aligned} P_G(x_1,\ldots,x_n)&=(1/|G|)\sum_{\tau\in G}\mathrm{ind}(\tau)\\ &=(1/|G|)\sum_{\tau\in G}x_1^{e_1(\tau)}x_2^{e_2(\tau)}\ldots x_n^{e_n(\tau)}, \end{aligned}$$

and so

$$\begin{aligned} P_G(q,\ldots,q)&=(1/|G|)\sum_{\tau\in G}q^{e_1(\tau)+e_2(\tau)+\cdots+e_n(\tau)}\\ &=(1/|G|)\sum_{\tau\in G}q^{t(\tau)}. \end{aligned}$$

■

Theorem 3.6.7 (Pólya) Let $G\le \mathrm S_X$, where $|X|=n$, let $|\mathscr C|=q$, and, for each $i\ge 1$, define $\sigma_i=c_1^i+\cdots+c_q^i$. Then the number of $(q,G)$-colorings of $X$ with $f_r$ elements of color $c_r$, for every $r$, is the coefficient of $c_1^{f_1}c_2^{f_2}\cdots c_q^{f_q}$ in $P_G(\sigma_1,\ldots,\sigma_n)$.

■■■■■■■■■■■■■■■■■■■■■■■■■

下一篇: GTM148 抄书笔记 Part II.