Knights of the Round Table

# Description
给定若干骑士和他们之间的仇恨关系，规定召开圆桌会议时，两个有仇恨的骑士不能坐在相邻位置，且召开一次圆桌会议的骑士人数必须为奇数，求有多少骑士永远不可能参加某一次圆桌会议。

# Format

## Input
多组数据，每组数据先给出N，M代表N个骑士和M组关系

接下来M行，每行两个数字

整个测试以0 0结束

1 ≤ n ≤ 1000

1 ≤ m ≤ 1000000

## Output
如题

# Samples

```input1
5 5
1 4
1 5
2 5
3 4
4 5
0 0
```

```output1
2
```

 

 

 题解：

建图时，对互相不憎恨的两人之间连一条边。

对任意一名骑士来说，他要能出席某次会议则他左右的人都不能与他互相憎恨。

将每次参加会议的所有人（不一定是整个骑士团，只需人数>=3且为奇数）看做一个点双联通分量，那么每个点都至少有两个点与他相邻。即需要保证双联通分量中存在奇圈。

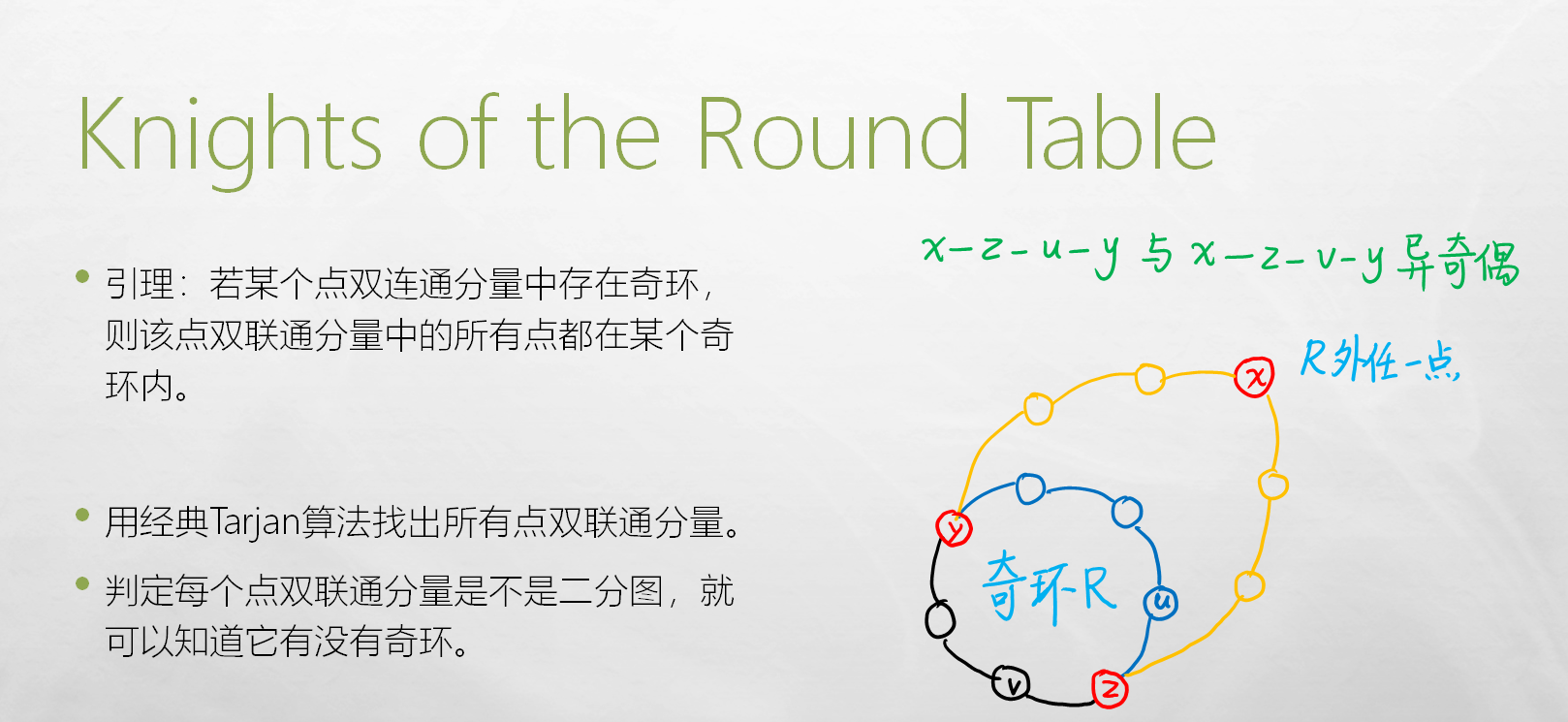
因为只要点双连通分量中存在奇圈，那么这个分量中所有的点都可以出现在奇圈上。

求奇圈时可以用到这样一个性质，一个图是二分图当且仅当图中不存在奇圈。

 

那么我们只需判断一个图是否是二分图就可以判断此图存在奇圈，可以用交替染色。
————————————————
版权声明：本文为CSDN博主「ConwayTian」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/Tsaid/article/details/6895808

 

 

#include <iostream>
#include <queue>
#include <stdio.h>
#include <cstring>
#include <vector>
const int maxn = 1e3 + 5;
const int inf = 0x3f3f3f3f;
using namespace std;
vector<int> g[maxn];
int gg[maxn][maxn];
int dfn[maxn], low[maxn], vis[maxn], Stack[maxn], inStack[maxn];
int color[maxn];
int len, cnt, ts;
int n, m;
void init(int n) 
{
	len = cnt = ts = 0;
	for (int i = 1; i <= n; ++i) g[i].clear();
	fill(vis, vis+n+1, 0);
	fill(dfn, dfn+n+1, 0);
	fill(gg[0], gg[0]+maxn*maxn, 0);
}
int check() 
{
	fill(color, color+maxn, -1);
	queue<int> que;
	for (int i = 1; i <= n; ++i) 
	{
		if (inStack[i]) 
		//找到一个在点双中的点 
		{
			que.push(i);
			color[i] = 0;
			break;
		}
	}
	while (!que.empty()) 
	 //做一次01染色 
	{
		int u = que.front();
		que.pop();
		for (int i = 0; i < (int)g[u].size(); ++i) 
		{
			int v = g[u][i];
			if (inStack[v] == 0) 
			    continue;
			if (color[v] == -1) 
			//如果没染过色，则染上一个与u不同的色彩 
			{
				color[v] = color[u] ^ 1;
				que.push(v);
			} 
			else 
			//如果染过了的话，并且与u一样
			//说明找到一个长度为奇数的环 
			if (color[v] == color[u]) 
			    return 1;
		}
	}
	return 0;
}
void tarjan(int u, int fa) 
{
	dfn[u] = low[u] = ++ts;
	Stack[len++] = u;
	for (int i = 0; i < (int)g[u].size(); ++i) 
	{
		int v = g[u][i];
		if (v == fa) continue;
		if (!dfn[v]) 
		{
			tarjan(v, u);
			low[u] = min(low[u], low[v]);
			if (dfn[u] <= low[v]) 
			{
				fill(inStack, inStack+n+1, 0);
				//instack为存放结果的 
				inStack[u] = 1;
				while (1) 
				{
					int top = Stack[--len];
					inStack[top] = 1;
					//top这个点在点双中 
					if (top == v) break;
				}
				if (check()) 
				//如果是一个奇数环的话 
				{
					for (int i = 1; i <= n; ++i) 
					{
						if (inStack[i])
							vis[i] = 1;
					}
				}
			}
		} else low[u] = min(low[u], dfn[v]);
	}
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	while (scanf("%d %d", &n, &m), n) {
		init(n);
		for (int i = 0; i < m; ++i) 
		{
			int u, v;
			scanf("%d%d", &u, &v);
			gg[u][v] = gg[v][u] = 1;
		}
		for (int i = 1; i <= n; ++i) {
			for (int j = 1; j <= n; ++j) {
				if (i == j || gg[i][j])
					continue;
				g[i].push_back(j);
			}
		}
		for (int i = 1; i <= n; ++i) 
		{
			if (dfn[i]) continue;
			tarjan(i, 0);
		}
		int ans = n;
		for (int i = 1; i <= n; ++i)
			ans -= vis[i];
		printf("%d\n", ans);
	}
	return 0;
}