任务处理--斜率优化Dp入门
https://blog.csdn.net/xingyeyongheng/article/details/25912663
你有n个任务需要处理,你有一台计算机能够处理这些任务,由于这些任务的特殊性,你只能按照顺序分批处理这些任务,不能先处理编号大的任务再处理编号小的。每个任务有一个处理难度值ai,计算机处理一批任务的总耗时是这批任务中所有任务的难度值之和的平方加上一个常量C。请你写一个程序合理的分批,使得计算机将所有任务都处理完的时间最少。
输入格式:第一行有2个整数n,c。第二行n个整数,a1,a2,a3,a4,a5,a6……an
输出格式:一行,输出最少的耗时。
Tasks.in
3 5
2 1 2
Tasks.out
23
说明:任务1,2一批,任务3一批。时间=(1+2)^2+5+2^2+5=23
数据范围:
40% n<=1000
100% n<=100000
所有数据的答案在INT64范围内
分析:
注意题目中出现了一句话“由于这些任务的特殊性,你只能按照顺序分批处理这些任务,不能先处理编号大的任务再处理编号小的。”这句话非常明显的道出了题目的无后效性,因而用动态规划解这样的题目,也就是顺理成章了。
下面我们不加推导的写出一个动态规划方程,相信大家都能够非常轻松的理解。
F[i]=min{f[j]+(sum[i]-sum[j])^2}+c
我们的目标是尽量将前面那一段更尽可的小,明显这个方程O(n^2),不能满足题目的要求。
设v[j]=f[j]+(sum[i]-sum[j])^2
我们不妨来考虑一下一般情况,即当x>y时且v[x]>v[y]。
于是乎 f[x]+(sum[i]-sum[x])^2>f[y]+(sum[i]-sum[y])^2
于是乎 f[x]-f[y]>(sum[i]-sum[y])^2-(sum[i]-sum[x])^2
于是乎 f[x]-f[y]>(2*sum[i]-sum[x]-sum[y])(sum[x]-sum[y])
于是乎 f[x]-f[y]>2*sum[i]*(sum[x]-sum[y])-sum[x]^2+sum[y]^2
于是乎 f[x]+sum[x]^2-f[y]-sum[y]^2>2*sum[i]*(sum[x]-sum[y])
于是乎 ((f[x]+sum[x]^2)-(f[y]+sum[y]^2))/sum[x]-sum[y]>2*sum[i]
不等式左边不难发现很像求斜率的公式,如果把其抽象成点,就成为了以sum[j]为x坐标,f[j]+sum[j]^2为y坐标
那么条件我们也可以知道了,就是将x和y这2个点连出一条线,这条线的斜率如果大于2*sum[i],
那么我们可以说在i的转移中v[x]>v[y],也就是说v[y]优于v[x],也就是说x标号小的结点应该被保留下来,
对于程序中来说就是队列头那种点。
下面我们需要挖掘这个特点对我们解题有什么作用。
我们可以建立一个队列,维护对于当前状态下的i,
队列中的相邻两个点的,它们的V值为递增状态
并且队列中的队首元素当前f[i]的转移元素。
如何选择满足条件的转移元素?
对于当前一个队列,可能不满足队首元素是我们需要的元素,
因为对于以前的某个i,当前队首元素可能比次首元素优,
但是现在由于sum[i]不断增大,它可能没有次首元素优,
我们可以将队首元素y和次首元素x之间直线的斜率求出,
如果其满足>2*sum[i],那么它仍然满足它是最优的条件,
如果不满足>2*sum[i],那么这个点就再也无法比次首元素优了(因为sum[i]是不断递增的),
那么我们可以将这个队首元素y放心的删去。这样判断,直到有满足条件的为止。
如何插入元素,并且维护队列?
当我们算出一个新的f[i]的时候,为了“造福后代”,我们需要将其加入到队列中,
加入队列后有2种情况(如下图1及图2):
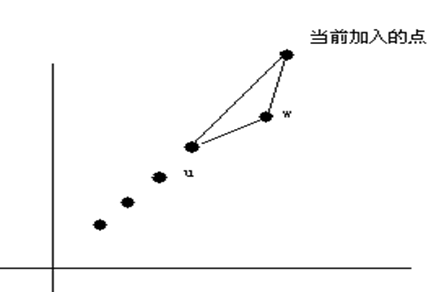
(图1)
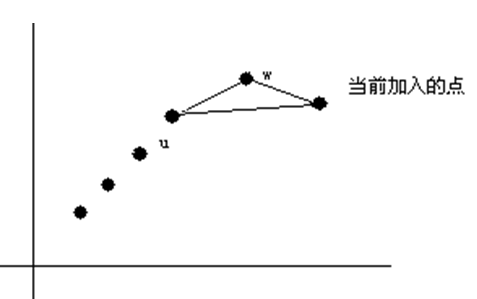
(图2)
假设我们设最后一个点为w,倒数第二个点为u。
图1中因为新加入的点与原队列中最后一个点构成的线段的斜率比原来最后一条线段的斜率大,
因为当前情况下w有意义,这样的情况的队列就是一个满足条件的队列。
图2中与图1正好相反,所以这样加入一个新的点,(这个新点与W之间的斜率不满足上面那个式子,
则说明这个新点比W更优,W的存在是没有意义的)会使得w这个点失去意义,
所以我们可以删掉w这个点,再不断做下去,知道最后几个点出现左图情况就可以了。
解决了上面2个问题,队列也就维护出来了,动态规划转移也可以完成了,下面我们来分析一下时间复杂度。
因为每个元素最多进队列一次,出队列一次,因此进行队列操作的复杂度是O(n),状态O(n)级别,转移取队首元素O(1)完成,动态规划复杂度也是O(n),所以总的复杂度为O(n)。
到此这个题目已经完美解决。
var
sum , f : array[0..100001] of int64;
list : array[0..100001] of longint;
n , c , head , tail : longint;
procedure init;
var
i , temp : longint;
begin
readln( n , c );
fillchar( sum , sizeof( sum ) , 0 );
for i := 1 to n do
begin
read( temp );
sum[i] := sum[i - 1] + temp;
end;
readln;
end;
function getk( a , b : longint ) : double;
//a,b..........i
begin
getk := ( f[b] - f[a] + sqr( sum[b] ) - sqr( sum[a] ) )
/ ( sum[b] - sum[a] );
end;
procedure del( now : longint );
begin
while ( head < tail ) and ( getk( list[head] , list[head + 1] ) < now ) do
inc( head );
end;
procedure add( now : longint );
var
t1 , t2 : double;
begin
repeat
if head >= tail then
break;
t1 := getk( list[tail - 1] , list[tail] );
t2 := getk( list[tail] , now );
if t1 < t2 then //对应图1
break
else //对应图2
dec( tail );
until false;
inc( tail );
list[tail] := now;
end;
procedure Dp;
var
i , temp : longint;
begin
head := 1;
tail := 1;
fillchar( list , sizeof( list ) , 0 );
for i := 1 to n do
begin
del( sum[i] * 2 );
//当i的值增加sum[i]变大,这时队列头结点有可能不再是最优决策,
//这时要删除头结点.找到一个最优的决策
f[i] := f[list[head]] + sqr( sum[i] - sum[list[head]] ) + c;
add( i );
end;
end;
procedure print;
begin
writeln( f[n] );
end;
procedure main;
begin
init;
Dp;
print;
end;
begin
main;
end.
#include<bits/stdc++.h>
#define N 500005
#define int long long
using namespace std;
int n,c,f[N],q[N],s[N],l,r;
double calc(int a,int b){return 1.0*(f[a]+pow(s[a],2)-f[b]-pow(s[b],2))/(s[a]-s[b]);}
signed main(){
scanf("%lld%lld",&n,&c);
for(int i=1,a;i<=n;i++){
scanf("%lld",&a);
s[i]=s[i-1]+a;
}
memset(f,0x3f,sizeof(f));
f[0]=0,l=r=1;
for(int i=1;i<=n;i++){
while(l<r&&calc(q[l],q[l+1])<2*s[i])l++;
f[i]=f[q[l]]+pow(s[i]-s[q[l]],2)+c;
while(l<r&&calc(q[r],i)<calc(q[r-1],i))r--;
q[++r]=i;
}
printf("%lld",f[n]);
return 0;
}
HNOI玩具装箱

#include <cstdio>
#include <algorithm>
const int N=5e4+5;
int n,L,c[N],q[N];
long long sum[N],x[N],y[N],f[N];
long long sqr(long long x) {
return x*x;
}
double slope(int i,int j) {
return 1.0*((f[i]+sqr(y[i]))-(f[j]+sqr(y[j])))/(y[i]-y[j]);
}
int main() {
scanf("%d%d",&n,&L);
x[0]=0,y[0]=1+L;
for(int i=1;i<=n;++i) {
scanf("%d",&c[i]);
sum[i]=sum[i-1]+c[i],x[i]=sum[i]+i,y[i]=sum[i]+i+1+L;
}
int l=1,r=0;
f[0]=q[++r]=0;
for(int i=1;i<=n;++i) {
while(l<r&&slope(q[l],q[l+1])<=2*x[i]) ++l;
f[i]=f[q[l]]+sqr(x[i]-y[q[l]]);
while(l<r&&slope(q[r-1],q[r])>=slope(q[r],i)) --r;
q[++r]=i;
}
printf("%lld\n",f[n]);
return 0;
}
还可以看下
https://www.cnblogs.com/terribleterrible/p/9669614.html
https://blog.csdn.net/zsyzClb/article/details/92782050?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param


 浙公网安备 33010602011771号
浙公网安备 33010602011771号