D - Common Subsequence

求两个字符串的最长公共序列，输出这个序列的长度。

A subsequence of a given sequence is the given sequence with some elements (possible none) left out. Given a sequence X = <x1, x2, ..., xm> another sequence Z = <z1, z2, ..., zk> is a subsequence of X if there exists a strictly increasing sequence <i1, i2, ..., ik> of indices of X such that for all j = 1,2,...,k, xij = zj. For example, Z = <a, b, f, c> is a subsequence of X = <a, b, c, f, b, c> with index sequence <1, 2, 4, 6>. Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y.
The program input is from a text file. Each data set in the file contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct. For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.

Input

abcfbc abfcab
programming contest 
abcd mnp

Output

4
2
0

列如：abcfbc abfcab

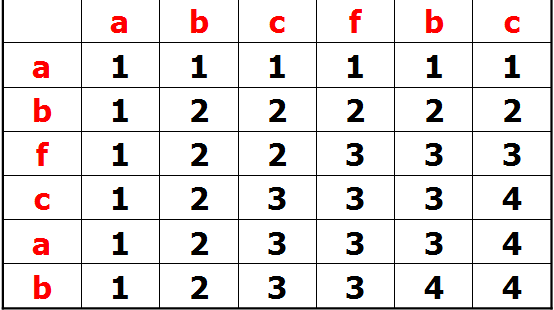
F[i][j]=F[i-1][j-1]+1；（a[i]==b[j]）

F[i][j]=max(F[i-1][j],F[i][j-1])(a[i]!=b[j]);

n由于F(i,j)只和F(i-1,j-1), F(i-1,j)和F(i,j-1)有关, 而在计算F(i,j)时, 只要选择一个合适的顺序, 就可以保证这三项都已经计算出来了, 这样就可以计算出F(i,j). 这样一直推到f(len(a),len(b))就得到所要求的解了.

LCS算法：

　　1、序列str1和序列str2

　　　　·长度分别为m和n；
　　　　·创建1个二维数组L[m.n]；
　　　　·初始化L数组内容为0
　　　　·m和n分别从0开始，m++，n++循环：
　　　　- 如果str1[m] == str2[n]，则L[m,n] = L[m - 1, n -1] + 1；
　　　　- 如果str1[m] != str2[n]，则L[m,n] = max{L[m,n - 1]，L[m - 1, n]}
　　　　·最后从L[m,n]中的数字一定是最大的，且这个数字就是最长公共子序列的长度
　　　　·从数组L中找出一个最长的公共子序列。

　　2、从数组L中查找一个最长的公共子序列

　　　　i和j分别从m，n开始，递减循环直到i = 0，j = 0。其中，m和n分别为两个串的长度。
　　　　·如果str1[i] == str2[j]，则将str[i]字符插入到子序列内，i–，j–；
　　　　·如果str1[i] != str[j]，则比较L[i,j-1]与L[i-1,j]，L[i,j-1]大，则j–，否则i–；（如果相等，则任选一个）

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
int dp[1001][1001];
char s1[1001],s2[1001];
int main()
{
    while(~scanf("%s %s",s1,s2))
    {
        int l1=strlen(s1);
        int l2=strlen(s2);
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=l1;i++)
        {
            for(int j=1;j<=l2;j++)
            {
                if(s1[i-1]==s2[j-1])
                dp[i][j]=dp[i-1][j-1]+1;
                else
                dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
            }
        }
        printf("%d\n",dp[l1][l2]);
    }
}