CF 1131A,1131B,1131C,1131D,1131F(Round541 A,B,C,D,F)题解
A. Sea Battle
In order to make the "Sea Battle" game more interesting, Boris decided to add a new ship type to it. The ship consists of two rectangles. The first rectangle has a width of w1w1 and a height of h1h1, while the second rectangle has a width of w2w2 and a height of h2h2, where w1≥w2w1≥w2. In this game, exactly one ship is used, made up of two rectangles. There are no other ships on the field.
The rectangles are placed on field in the following way:
- the second rectangle is on top the first rectangle;
- they are aligned to the left, i.e. their left sides are on the same line;
- the rectangles are adjacent to each other without a gap.
See the pictures in the notes: the first rectangle is colored red, the second rectangle is colored blue.
Formally, let's introduce a coordinate system. Then, the leftmost bottom cell of the first rectangle has coordinates (1,1)(1,1), the rightmost top cell of the first rectangle has coordinates (w1,h1)(w1,h1), the leftmost bottom cell of the second rectangle has coordinates (1,h1+1)(1,h1+1) and the rightmost top cell of the second rectangle has coordinates (w2,h1+h2)(w2,h1+h2).
After the ship is completely destroyed, all cells neighboring by side or a corner with the ship are marked. Of course, only cells, which don't belong to the ship are marked. On the pictures in the notes such cells are colored green.
Find out how many cells should be marked after the ship is destroyed. The field of the game is infinite in any direction.
Four lines contain integers w1,h1,w2w1,h1,w2 and h2h2 (1≤w1,h1,w2,h2≤1081≤w1,h1,w2,h2≤108, w1≥w2w1≥w2) — the width of the first rectangle, the height of the first rectangle, the width of the second rectangle and the height of the second rectangle. You can't rotate the rectangles.
Print exactly one integer — the number of cells, which should be marked after the ship is destroyed.
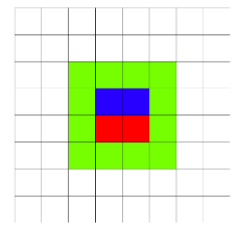
2 1 2 1
12
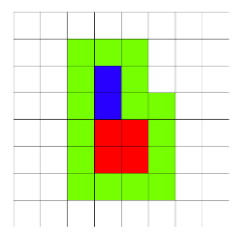
2 2 1 2
16
In the first example the field looks as follows (the first rectangle is red, the second rectangle is blue, green shows the marked squares):
In the second example the field looks as:
题解:题意就是让你求围绕两个矩形一周所占的方格数;答案就是不论上面的方格小于还是等于下面的方格的宽,都是2*(w1+2+h1+h2)
参考代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int INF=0x3f3f3f3f; 5 ll w1,h1,w2,h2,ans; 6 int main() 7 { 8 ans=0; 9 scanf("%lld%lld%lld%lld",&w1,&h1,&w2,&h2); 10 ans=2*(w1+h1+h2+2); 11 printf("%lld\n",ans); 12 return 0; 13 }
B. Draw!
You still have partial information about the score during the historic football match. You are given a set of pairs (ai,bi)(ai,bi), indicating that at some point during the match the score was "aiai: bibi". It is known that if the current score is «xx:yy», then after the goal it will change to "x+1x+1:yy" or "xx:y+1y+1". What is the largest number of times a draw could appear on the scoreboard?
The pairs "aiai:bibi" are given in chronological order (time increases), but you are given score only for some moments of time. The last pair corresponds to the end of the match.
The first line contains a single integer nn (1≤n≤100001≤n≤10000) — the number of known moments in the match.
Each of the next nn lines contains integers aiai and bibi (0≤ai,bi≤1090≤ai,bi≤109), denoting the score of the match at that moment (that is, the number of goals by the first team and the number of goals by the second team).
All moments are given in chronological order, that is, sequences xixi and yjyj are non-decreasing. The last score denotes the final result of the match.
Print the maximum number of moments of time, during which the score was a draw. The starting moment of the match (with a score 0:0) is also counted.
3
2 0
3 1
3 4
2
3
0 0
0 0
0 0
1
1
5 4
5
In the example one of the possible score sequences leading to the maximum number of draws is as follows: 0:0, 1:0, 2:0, 2:1, 3:1, 3:2, 3:3, 3:4.
题解:给你两个人在比赛中某些时刻的得分比,让你判断最多有多少时刻,两个人的比分是相同的;
对两个时刻之间处理即可:现在的最小值-前一时刻的最大值,(如果前一时刻是比分不相同的,再加一)
参考代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 int n; 5 ll x,y,cx,cy,ans; 6 int main() 7 { 8 cin>>n; 9 ans=1;cx=cy=0; 10 for(int i=1;i<=n;++i) 11 { 12 cin>>x>>y; 13 ll L=max(cx,cy); 14 ll R=min(x,y); 15 if(R>=L) 16 { 17 if(cx==cy) ans+=(R-L); 18 else ans+=(R-L+1); 19 } 20 cx=x;cy=y; 21 } 22 cout<<ans<<endl; 23 24 25 return 0; 26 }
C. Birthday
Cowboy Vlad has a birthday today! There are nn children who came to the celebration. In order to greet Vlad, the children decided to form a circle around him. Among the children who came, there are both tall and low, so if they stand in a circle arbitrarily, it may turn out, that there is a tall and low child standing next to each other, and it will be difficult for them to hold hands. Therefore, children want to stand in a circle so that the maximum difference between the growth of two neighboring children would be minimal possible.
Formally, let's number children from 11 to nn in a circle order, that is, for every ii child with number ii will stand next to the child with number i+1i+1, also the child with number 11 stands next to the child with number nn. Then we will call the discomfort of the circle the maximum absolute difference of heights of the children, who stand next to each other.
Please help children to find out how they should reorder themselves, so that the resulting discomfort is smallest possible.
The first line contains a single integer nn (2≤n≤1002≤n≤100) — the number of the children who came to the cowboy Vlad's birthday.
The second line contains integers a1,a2,…,ana1,a2,…,an (1≤ai≤1091≤ai≤109) denoting heights of every child.
Print exactly nn integers — heights of the children in the order in which they should stand in a circle. You can start printing a circle with any child.
If there are multiple possible answers, print any of them.
5 2 1 1 3 2
1 2 3 2 1
3 30 10 20
10 20 30
In the first example, the discomfort of the circle is equal to 11, since the corresponding absolute differences are 11, 11, 11 and 00. Note, that sequences [2,3,2,1,1][2,3,2,1,1] and [3,2,1,1,2][3,2,1,1,2] form the same circles and differ only by the selection of the starting point.
In the second example, the discomfort of the circle is equal to 2020, since the absolute difference of 1010 and 3030 is equal to 2020.
题解:重新排列这些数,是其围城一个环相邻差值和最小;
分奇数位和偶数位分别放在两边;
参考代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define clr(a,val) memset(a,val,sizeof(a)) 5 #define fi first 6 #define se second 7 #define pb push_back 8 const int INF=0x3f3f3f3f; 9 int n,a[105],b[105]; 10 int main() 11 { 12 int n; 13 scanf("%d",&n); 14 for(int i=1;i<=n;i++) scanf("%d",&a[i]); 15 sort(a+1,a+1+n); 16 for(int i=1;i<=n;i++) 17 { 18 if(i&1) 19 b[i/2+1]=a[i]; 20 else b[n-i/2+1]=a[i]; 21 } 22 for(int i=1;i<=n;i++) printf("%d ",b[i]); 23 printf("\n"); 24 return 0; 25 }
D. Gourmet choice
Mr. Apple, a gourmet, works as editor-in-chief of a gastronomic periodical. He travels around the world, tasting new delights of famous chefs from the most fashionable restaurants. Mr. Apple has his own signature method of review — in each restaurant Mr. Apple orders two sets of dishes on two different days. All the dishes are different, because Mr. Apple doesn't like to eat the same food. For each pair of dishes from different days he remembers exactly which was better, or that they were of the same quality. After this the gourmet evaluates each dish with a positive integer.
Once, during a revision of a restaurant of Celtic medieval cuisine named «Poisson», that serves chestnut soup with fir, warm soda bread, spicy lemon pie and other folk food, Mr. Apple was very pleasantly surprised the gourmet with its variety of menu, and hence ordered too much. Now he's confused about evaluating dishes.
The gourmet tasted a set of nn dishes on the first day and a set of mm dishes on the second day. He made a table aa of size n×mn×m, in which he described his impressions. If, according to the expert, dish ii from the first set was better than dish jj from the second set, then aijaij is equal to ">", in the opposite case aijaij is equal to "<". Dishes also may be equally good, in this case aijaij is "=".
Now Mr. Apple wants you to help him to evaluate every dish. Since Mr. Apple is very strict, he will evaluate the dishes so that the maximal number used is as small as possible. But Mr. Apple also is very fair, so he never evaluates the dishes so that it goes against his feelings. In other words, if aijaij is "<", then the number assigned to dish ii from the first set should be less than the number of dish jj from the second set, if aijaij is ">", then it should be greater, and finally if aijaij is "=", then the numbers should be the same.
Help Mr. Apple to evaluate each dish from both sets so that it is consistent with his feelings, or determine that this is impossible.
The first line contains integers nn and mm (1≤n,m≤10001≤n,m≤1000) — the number of dishes in both days.
Each of the next nn lines contains a string of mm symbols. The jj-th symbol on ii-th line is aijaij. All strings consist only of "<", ">" and "=".
The first line of output should contain "Yes", if it's possible to do a correct evaluation for all the dishes, or "No" otherwise.
If case an answer exist, on the second line print nn integers — evaluations of dishes from the first set, and on the third line print mmintegers — evaluations of dishes from the second set.
3 4 >>>> >>>> >>>>
Yes 2 2 2 1 1 1 1
3 3 >>> <<< >>>
Yes 3 1 3 2 2 2
3 2 == =< ==
No
In the first sample, all dishes of the first day are better than dishes of the second day. So, the highest score will be 22, for all dishes of the first day.
In the third sample, the table is contradictory — there is no possible evaluation of the dishes that satisfies it.
题解:题目就是给你n和m个数,给出这n和m个数的大小关系,让你求,最小有多少种数;
n和m映射到1~n+m这些数中;
对于"=",我们用并查集将他们缩点;
然后对">"和"<"进行建边,跑拓扑排序即可;
然后dp[i]:表示第i个数大小;
dp[e[x].to]=max(dp[e[x].to],dp[x]+1);
最后依次输出即可;
参考代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define clr(a,val) memset(a,val,sizeof(a)) 5 #define fi first 6 #define se second 7 #define pb push_back 8 const int INF=0x3f3f3f3f; 9 const int N=2e3+7,M=2e6+7; 10 struct data{ 11 int to,next; 12 } e[M]; 13 int head[N],cnt,dp[N],x,tot,n,m; 14 int q[N],t,w,fa[N],ans[N],in[N]; 15 char mp[N/2][N/2]; 16 int find(int x){ return x==fa[x]?x:fa[x]=find(fa[x]); } 17 void ins(int u,int v) 18 { 19 e[++cnt].to=v; 20 e[cnt].next=head[u]; 21 head[u]=cnt; 22 in[v]++;//入度 23 } 24 int main() 25 { 26 scanf("%d%d",&n,&m); 27 for(int i=1;i<=n;++i) scanf("%s",mp[i]+1); 28 for(int i=1;i<=n+m;++i) fa[i]=i; 29 for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) if(mp[i][j]=='=') fa[find(i)]=find(n+j);//缩点 30 for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) 31 { 32 if(mp[i][j]=='>') ins(find(n+j),find(i)); 33 else if(mp[i][j]=='<') ins(find(i),find(n+j)); 34 } 35 36 for(int i=1;i<=n+m;++i) if(find(i)==i) tot++; 37 for(int i=1;i<=n+m;++i) if(!in[i]&&find(i)==i) q[w++]=i,dp[i]=1; 38 while(t!=w)//拓扑 39 { 40 x=q[t++]; 41 for(int i=head[x];i;i=e[i].next) 42 { 43 dp[e[i].to]=max(dp[e[i].to],dp[x]+1); 44 if(--in[e[i].to]==0) q[w++]=e[i].to; 45 } 46 } 47 if(t!=tot) { puts("No");return 0;} 48 else 49 { 50 puts("Yes"); 51 for(int i=1;i<=n;++i) printf("%d%c",dp[find(i)],i==n?'\n':' '); 52 for(int i=1;i<=m;++i) printf("%d%c",dp[find(i+n)],i==m?'\n':' '); 53 } 54 return 0; 55 }
F. Asya And Kittens
Asya loves animals very much. Recently, she purchased nn kittens, enumerated them from 11 and nn and then put them into the cage. The cage consists of one row of nn cells, enumerated with integers from 11 to nn from left to right. Adjacent cells had a partially transparent partition wall between them, hence there were n−1n−1 partitions originally. Initially, each cell contained exactly one kitten with some number.
Observing the kittens, Asya noticed, that they are very friendly and often a pair of kittens in neighboring cells wants to play together. So Asya started to remove partitions between neighboring cells. In particular, on the day ii, Asya:
- Noticed, that the kittens xixi and yiyi, located in neighboring cells want to play together.
- Removed the partition between these two cells, efficiently creating a single cell, having all kittens from two original cells.
Since Asya has never putted partitions back, after n−1n−1 days the cage contained a single cell, having all kittens.
For every day, Asya remembers numbers of kittens xixi and yiyi, who wanted to play together, however she doesn't remember how she placed kittens in the cage in the beginning. Please help her and find any possible initial arrangement of the kittens into nn cells.
The first line contains a single integer nn (2≤n≤1500002≤n≤150000) — the number of kittens.
Each of the following n−1n−1 lines contains integers xixi and yiyi (1≤xi,yi≤n1≤xi,yi≤n, xi≠yixi≠yi) — indices of kittens, which got together due to the border removal on the corresponding day.
It's guaranteed, that the kittens xixi and yiyi were in the different cells before this day.
For every cell from 11 to nn print a single integer — the index of the kitten from 11 to nn, who was originally in it.
All printed integers must be distinct.
It's guaranteed, that there is at least one answer possible. In case there are multiple possible answers, print any of them.
5 1 4 2 5 3 1 4 5
3 1 4 2 5
The answer for the example contains one of several possible initial arrangements of the kittens.
The picture below shows how the cells were united for this initial arrangement. Note, that the kittens who wanted to play together on each day were indeed in adjacent cells.

题解:题意就是一些人站成一排,然后n-1个关系,x,y:表示x和y想玩;
让你给出他们初始的顺序;
并查集,用g[i]表示i块最左边的人,每次合并块,保证相对位置即可;
参考代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define clr(a,val) memset(a,val,sizeof(a)) 4 #define ll long long 5 #define PI acos(-1.0) 6 #define mp make_pair 7 #define pb push_back 8 const int INF=0x3f3f3f3f; 9 const int maxn=2e5+10; 10 int n,fa[maxn],r[maxn],g[maxn],x,y; 11 int find(int x){return x==fa[x]? x:fa[x]=find(fa[x]);} 12 int main() 13 { 14 scanf("%d",&n); 15 for(int i=1;i<=n;++i) fa[i]=i,r[i]=i; 16 for(int i=1;i<n;++i) 17 { 18 scanf("%d%d",&x,&y); 19 int fx=find(x),fy=find(y); 20 g[r[fx]]=fy;r[fx]=r[fy];fa[fy]=fx; 21 } 22 for(int i=find(1);i;i=g[i]) printf("%d ",i); 23 printf("\n"); 24 return 0; 25 }
参考代码:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号