剑指offer——Day23 数学（简单）

Day23 2023.2.5 数学（简单）

剑指Offer 39. 数组中出现次数超过一半的数字

自己实现

因为考虑到这个数字起码有数组长度的一般那么多，那么如果把所有该数字放在一起，它势必会占据数组的中点，因此自己实现的方法就是将数组进行排序，然后直接返回排序后的数组中点即可

代码如下：

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        return nums[nums.size()/2];
    }
};

代码表现

用排序就肯定有点慢了，看看题解

题解

方法一：数组排序法（就是自己实现的方法）

方法二：哈希表统计法：遍历数组，用HashMap统计各数字数量即可

方法三：摩尔投票法（下面详述）

摩尔投票法核心理念为票数正负抵消。此方法是本题的最佳解法

设输入数组nums的超过一半数量以上的数为x，数组长度为n

推论一：若记x的票值为+1，非x的票值为-1，则一定所有数字的票值和 > 0

推论二：若数组的前a个数字的票值和 = 0，则数组剩余(n-a)个数字的票值和一定仍然 > 0，即后(n-a)个数字的数量最多的数字仍为x

算法流程

1. 初始化：票数统计votes=0，众数x
2. 循环：遍历数组nums中的每个数字num
   1. 当票数votes等于0，则假设当前数字num是超过一半数量的数
   2. 当num=x时，票数votes自增1；反之，自减1
3. 返回值：返回x即可

代码如下：

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int x, votes=0;
        for(int num:nums){
            if(votes==0)x=num;
            votes+= (num==x?1:-1);
        }
        return x;
    }
};

代码表现

要快多了

hint

• 其实这个还是用的一个排除的方法，将众数和非众数通过票数进行不断地抵消，最后剩下的一定就是那个众数。这样的思路可以用在占据超过一半容量的情况下，当然，也仅限于超过一半的情况下

剑指Offer 66. 构建乘积数组

自己实现

这个题目最难的要求就是不能使用除法，目前想到的方法就是直接暴力求解，这个肯定是不行的，直接看题解了

题解

题解给了一张图如下，看了就恍然大悟了

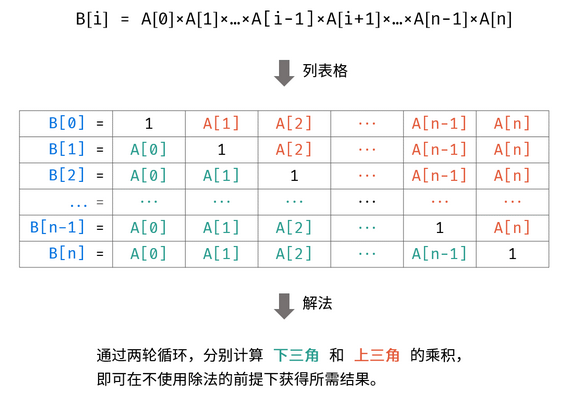
其实这就有动态规划的味道了，只是将动态规划蕴藏在了这个逐乘的过程中，而且其中包含了两个dp数组，分开维护最后再乘起来即可

题解用的是两个循环来做，自己参考这个表试试能不能一个循环做出来

但是必须要同时使用两个dp在同一个下标的结果才能得到B对应下标的值，一个循环好像有点勉强，看看参考

但其实一个循环和两次循环的时间消耗都是一样的，傻子……

只是一次循环的想法是，每一个下标的B值不是一次就要乘到位，先乘一边再等着乘另一边，给循环部分的代码作为参考：

for(int i = 0; i < len; i++){
        b[i] *= left;
        left *= a[i];           // 持有左边的所有数的乘积
        b[len - i - 1] *= right;
        right *= a[len -i - 1];  // 持有右边的所有数的乘积
}

而两次循环的代码如下：

class Solution {
public:
    vector<int> constructArr(vector<int>& a) {
        int len=a.size();
        vector<int> B(len,1);
        if(len==0)return B;
        int tmp=1;
        for(int i=1;i<len;i++){
            B[i]=B[i-1]*a[i-1];
        }
        for(int i=len-2;i>=0;i--){
            tmp*=a[i+1];
            B[i]*=tmp;
        }
        return B;
    }
};

代码表现

hint:

• 还是用到了dp的思想，这种逐乘逐加的通常适配dp，当然，这个地方的另一要点就是将dp过程划分出两个dp数组来进行。
• 其实dp很多时候需要的是二维的图示，光是看某一条（某个一维情况）很能看出来怎么用dp，就像这个题的题解，列出一个表，一看就知道是dp了，再结合这个地方被分裂成两个dp来做，就ok的。多沉淀