剑指offer——Day09动态规划（中等）

Day9 2022.11.15 动态规划（中等）

42.连续子数组的最大和

自己实现

想用动态规划，但是基于前一天的《63.股票的最大利润》的思路，有点想不清楚怎么满足“连续子数组”的要求，看数组了。

题解

解决这个连续子数组就是将dp[i]的每个元素定义为以第i个元素为结尾的子数组中的最大利润。有两种情况：

• 当dp[i-1]>0时，执行dp[i] = dp[i-1] + nums[i]
• 当dp[i-1]≤0时，执行dp[i] = nums[i]（因为当前一个元素为结尾的子数组的最大利润都是负的，就证明带上前一个元素会带来反作用，所以就不用和前面连续了）

代码如下：

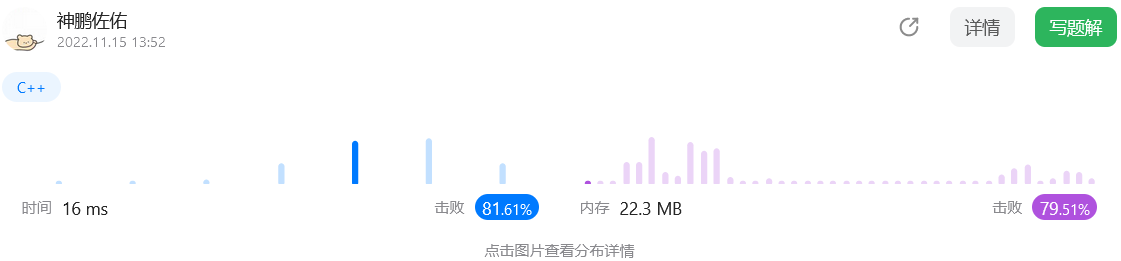
代码表现

hint：

• 对于需要连续的情况，在普通动态规划的基础上去考虑什么时候需要连续，什么时候可以直接不连续。形如这个题就是，如果前一个元素为结尾的子数组都只能带来副作用的话，那直接不要；但凡前一个元素能带来一点作用，那就都要。这就将问题转化为了简单的大于小于零的情况，容易考虑了。

47.礼物的最大价值

自己实现

又傻了，看的题解，后面可以再温故一下

题解

这个题目就用原来的二维数组来做即可。每个位置只有可能由这个位置的左边和上面走到，因此转移方程就出来了！很简单的：f(i,j)=max[f(i,j−1),f(i−1,j)]+grid(i,j)

另外，还有一个比较巧妙的就是，因为这个题目规定只能向右和向下走，所以第一行和第一列一定是没有多种情况的，这是比较特殊的，放在大遍历里面可能会将其变得复杂，所以可以提前拿出来直接初始化。

代码如下：

class Solution {
public:
    int maxValue(vector<vector<int>>& grid) {
        int i,j;
        if(grid.size()==0)return 0;
        for(i=1;i<grid.size();i++)grid[i][0]+=grid[i-1][0];
        for(j=1;j<grid[0].size();j++)grid[0][j]+=grid[0][j-1];
        for(i=1;i<grid.size();i++)
        {
            for(j=1;j<grid[0].size();j++)
            {
                grid[i][j]+=(grid[i-1][j]>grid[i][j-1]?grid[i-1][j]:grid[i][j-1]);
            }
        }
        return grid[grid.size()-1][grid[0].size()-1];
    }
};

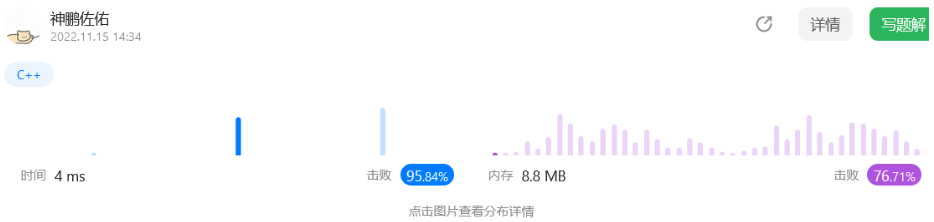
代码表现

时间和空间都挺不错

hint：

• 还是拿住某一个点分析它和前一种情况的关系啊啊啊啊！！！傻
• 当然，一些特殊情况可以单独提出来先初始化，例如代码中的Line6、7