剑指offer——Day07搜索与回溯算法（简单）

Day7 2022.11.13 树的子结构

26.树的子结构

自己实现

应该是用递归，具体没有思路，直接看题解了

题解

用两个函数isSubStructure()和recur()来解决。就不断去递归比较A的子树与B即可。看代码应该就能理解（注意空树不是任意一个树的子结构）

代码如下：

class Solution {
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        return (A!=NULL&&B!=NULL) && (recur(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B));
    }
    bool recur(TreeNode* A, TreeNode* B)
    {
        if(B==NULL) return true;
        if(A==NULL || A->val!=B->val)return false;
        return recur(A->left,B->left) && recur(A->right, B->right);
    }
};

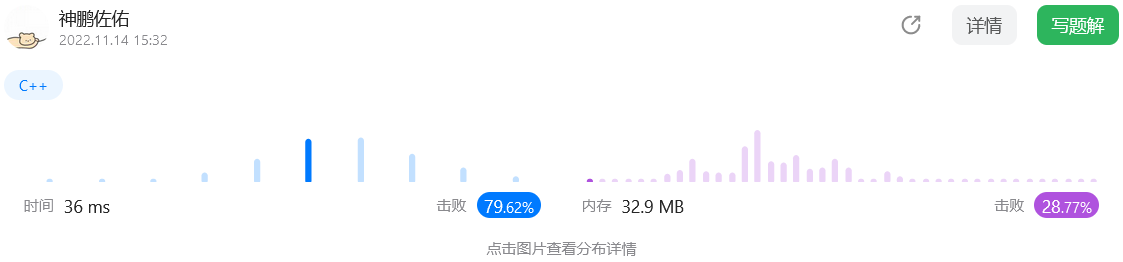
代码实现

时间不稳定 正常的

hint：

• 递归设置好出口就最关键。

27.二叉树的镜像

自己实现

这个和斜堆的过程是基本一样的，就不详细说了（递归实现）

代码如下：

class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root==NULL)return root;
        recur(root);
        return root;
    }
    void recur(TreeNode* root)
    {
        if(root==NULL)return;
        recur(root->left);
        recur(root->right);
        swap(root);
    }
    void swap(TreeNode* root)
    {
        TreeNode* tmp=root->left;
        root->left=root->right;
        root->right=tmp;
    }
};

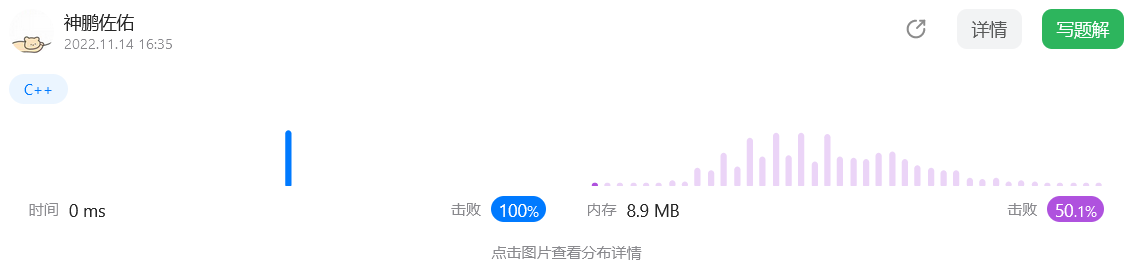
代码表现

时间不稳定，但是递归挺好用的

题解

题解就是正向地不断入栈、交换、出栈。比较巧妙的一点在于入栈时先左儿子再右儿子，然后马上交换（左儿子变成右儿子，右儿子变成左儿子），这样出栈的时候仍然是先出左儿子再出右儿子。（但其实好像这个顺序没啥关系...）

代码如下：

class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root==NULL)return root;
        vector<TreeNode*> vec;
        vec.push_back(root);
        while(vec.size()!=0)
        {
            TreeNode* now=vec[vec.size()-1];
            vec.pop_back();
            if(now->left!=NULL)vec.push_back(now->left);
            if(now->right!=NULL)vec.push_back(now->right);
            TreeNode* tmp=now->left;
            now->left=now->right;
            now->right=tmp;

        }
        return root;
    }
};

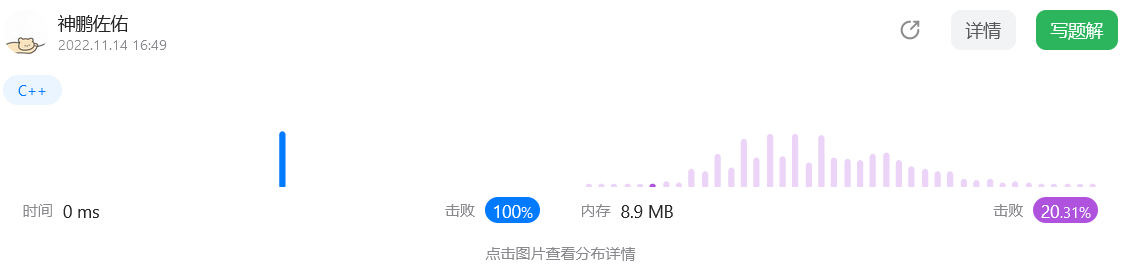
代码表现

时间不稳定，又能0ms，有鬼了...

hint：

• 递归的思想要多练习多去想，会自然很多
• 之前没有接触过正向地使用栈的思路，可以体验下，巧妙点可以看上文题解描述

28.对称的二叉树

自己实现

题目里其实给了思路了。先用递归复制一棵树出来，然后用这棵树递归得到其镜像树，再用递归比较镜像树和原来的树是否相等

代码如下

  class Solution {
  public:
	  bool isSymmetric(TreeNode* root) {
		  if (root == NULL)return true;
		  TreeNode* root0 = new TreeNode(root->val);
		  TreeNode* now0 = root0;
		  copy_recur(root, now0);
		  recur(root);
		  return comp_recur(root, root0);
	  }
	  void copy_recur(TreeNode* root, TreeNode* root0)
	  {
		  if (root == NULL)return;
		  if (root->left != NULL)root0->left = new TreeNode(root->left->val);
		  if (root->right != NULL)root0->right = new TreeNode(root->right->val);
		  copy_recur(root->left, root0->left);
		  copy_recur(root->right, root0->right);
	  }
	  void recur(TreeNode* root)
	  {
		  if (root == NULL)return;
		  recur(root->left);
		  recur(root->right);
		  swap(root);
	  }
	  void swap(TreeNode* root)
	  {
		  TreeNode* tmp = root->left;
		  root->left = root->right;
		  root->right = tmp;
	  }
	  bool comp_recur(TreeNode* root, TreeNode* root0)
	  {

		  if (root == NULL && root0 == NULL)return true;
		  if ((root == NULL && root0 != NULL) || (root != NULL && root0 == NULL))return false;
		  if (root->val != root0->val)return false;
		  if(!comp_recur(root->left, root0->left))return false;
		  if(!comp_recur(root->right, root0->right))return false;
		  return true;
	  }
  };

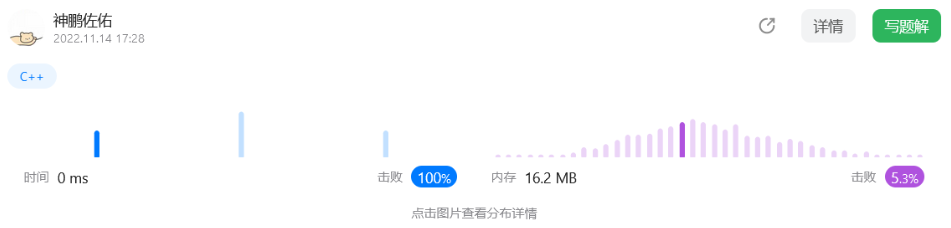
代码表现

题解

用递归简单地写出来了。用左儿子的左儿子和右儿子的右儿子比较&&用左儿子的右儿子和右儿子的左儿子比较。

代码如下：

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return root==NULL?true:recur(root->left,root->right);
    }
    bool recur(TreeNode* L,TreeNode* R)
    {
        if(L==NULL && R==NULL)return true;  //排除了两个都为NULL的情况
        if(L==NULL || R==NULL || L->val!=R->val)return false;
        return recur(L->left, R->right) && recur(L->right, R->left);
    }
};

代码表现

hint：

• 递归判断两棵树是否相等那里，Line38, 39卡了一下，可以记忆一下