剑指offer——Day05查找算法（中等）

Day5 2022.11.11 查找算法（中等）

04.二维数组中的查找

自己实现

简单的直接暴力遍历

代码如下：

class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        int i,j;
        for(i=0;i<matrix.size();i++)
        {
            for(j=0;j<matrix[i].size();j++)
            {
                if(matrix[i][j]==target)return true;
            }
        }
        return false;
    }
};

代码实现

确实慢...

题解

(nb)旋转！将二维矩阵旋转成二叉搜索树的形式。通过将矩阵逆时针旋转45°，将matrix[0][j_max-1]旋转到最高点，作为二叉搜索树的根节点，矩阵剩余部分就组成了二叉搜索树。即从根节点开始，往左儿子走(j--)数值就减小，右儿子走(i++)数值就增大。最终直到找到了这个数值或超出了这个数组的下标为止。示意图如下：

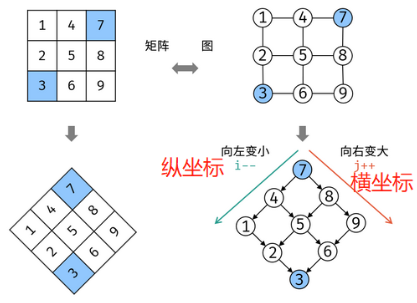
代码如下：

class Solution {
public:
	bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        if(matrix.size()==0 || matrix[0].size()==0)return false;    //记住要先判断是否为空
		int i = 0;
		int i_max = matrix.size();
		int j_max = matrix[0].size();
		int j = j_max - 1;
		while (i < i_max && j > -1)
		{
			if (target == matrix[i][j])return true;
			else if (target < matrix[i][j])j--;
			else i++;
		}
		return false;
	}
};

代码表现：

hint：

• 用矩阵来旋转45°得到二叉搜索树的思路真的很好，当然这个矩阵旋转后要符合往一个方向递减、往另一个方向递增，才能构成二叉搜索树的形式进行高效搜索
• 拿一个矩阵来直接用下标进行操作之前一定要先判断该矩阵是否为空，不然就容易像上述代码中的int j_max=matrix[0].size();一样，如果矩阵为空则不存在matrix[0]，下标就会超限
• 在操作矩阵时，多想一下是i还是j

11.旋转数组的最小数字

自己实现

最开始用二分法尝试了一下，但是写出来总有情况会不能做到，就选择简单利用它的局部升序性质了。即遍历数组，如果遇到突然减小的元素，则最小值就是这个元素；如果直到for循环结束都没找到，则为numbers[0]。

代码如下：

class Solution {
public:
    int minArray(vector<int>& numbers) {
        int min=9999;
        for(int i=0;i<numbers.size()-1;i++)
        {
            if(numbers[i]>numbers[i+1])return numbers[i+1];
        }
        return numbers[0];
    }
};

代码表现

不出意料地慢

题解

还是使用二分法。一个重要条件是左排序数组任一元素 ≥ 右排序数组任一元素具体过程如下：

1. 初始化： 声明 i, j 双指针分别指向nums数组左右两端

2. 循环二分：设m=(i+j) / 2为每次二分的中点（因为除法是向下取整，所以恒有i≤m＜j），三种情况

   a. 当nums[m]>nums[j] 时： m 一定在 左排序数组 中，即旋转点 x 一定在 [m + 1, j] 闭区间内，因此执行 i=m+1；

   b. 当nums[m]<nums[j] 时： m 一定在 右排序数组 中，即旋转点 x 一定在 [i, m] 闭区间内，因此执行 j=m；

   c. 当nums[m]=nums[j] 时： 无法判断 m 在哪个排序数组中，即无法判断旋转点 x 在 [i,m] 还是 [m+1,j] 区间中。解决方案： 执行 j=j−1 缩小判断范围，分析见下文。

3. 返回值：当i = j时跳出二分循环，并返回旋转点的值numbers[i]即可

*** 其中有一点值得提到的是为什么不用numbers[m]和numbers[i]作比较：

二分目的是判断 m 在哪个排序数组中，从而缩小区间。而在 nums[m]>nums[i]情况下，无法判断 m 在哪个排序数组中。本质上是由于 j 初始值肯定在右排序数组中； i 初始值无法确定在哪个排序数组中。举例如下：

代码如下：

class Solution {
public:
    int minArray(vector<int>& numbers) {
        int i=0;
        int j=numbers.size()-1;
        int m=0;
        while(i!=j)
        {
            m=(i+j)/2;
            if(numbers[m]>numbers[j])i=m+1;
            else if(numbers[m]<numbers[j])j=m;
            else j=j-1;
        }
        return numbers[i];
    }
};

代码表现：

hint：

• 排序数组的查找问题首先考虑使用二分法解决，可以将遍历法的线性时间复杂度降低到对数级别

50.第一个只出现一次的字符

自己实现

使用string容器的find()和rfind()方法来判断。从前往后遍历字符串，当find()==rfind()为true的时候证明已经找到第一个只出现过一次的字符了

代码如下

class Solution {
public:
    char firstUniqChar(string s) {
        int i;
        for(i=0;i<s.size();i++)
        {
            if(s.find(s[i])==s.rfind(s[i]))return s[i];
        }
        return ' ';
    }
};

代码实现

题解

使用哈希表，遍历字符串将每个字符存进map，并将其值设置为true。即将存入每个字符时，先判断map里面有没有这个key：若有，则将其值设置为false；若没有，则将其正常存入并赋值为true

代码如下：

class Solution {
public:
    char firstUniqChar(string s) {
        int i;
        unordered_map<char, bool> map;
        bool flag;
        for(i=0;i<s.size();i++)
        {
            flag=(map.find(s[i])==map.end());
            if(flag)map[s[i]]=true;
            else if(!flag)map[s[i]]=false;
        }
        for(i=0;i<s.size();i++)
        {
            if(map[s[i]]==true)return s[i];
        }
        return ' ';
    }
};

代码表现

这个时间表现其实算不得好，两次遍历感觉还不如自己实现的方法。

如果想对数据量较大的样例有时间的提高的话，可以使用有序哈希表，用一个vector来按照s的字符顺序来存储map的key应该有的顺序，按照这个顺序来检查map的每对键值，但是感觉和遍历字符串也相差不大。

hint：

• 调查一个类数组结构中是否有重复的元素仍然是采用哈希表比较普遍。