实验三实验报告
实验三
实验项目
项目一
- 完成教材P302 Searching.Java ,P305 Sorting.java中方法的测试
不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位
提交运行结果图(可多张)
实验用例设计以及结果显示:
![image]()
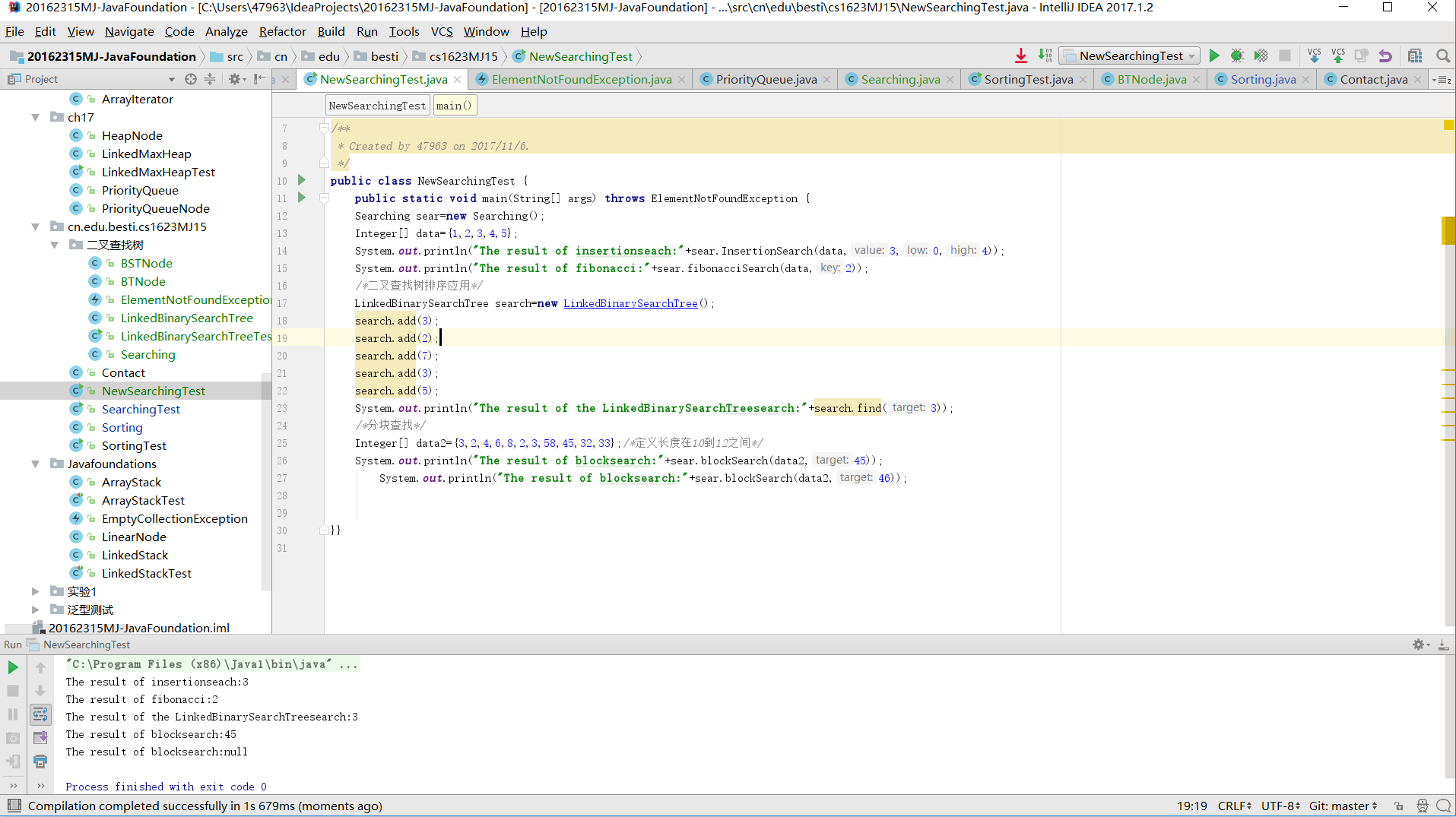
- 第一张图片:查找测试中第一个测试用正确,第二个有异常情况:有两个可输出选项只输出了一个;第三个超出查找边界,搜索项目里面不存在查找项。第四个查找目标只给出了一个信息不符合查找条件,异常;第五个给出了多余信息,但是Searching类排除了这个多余信息,并未将之作为查找条件正确。
![image]()
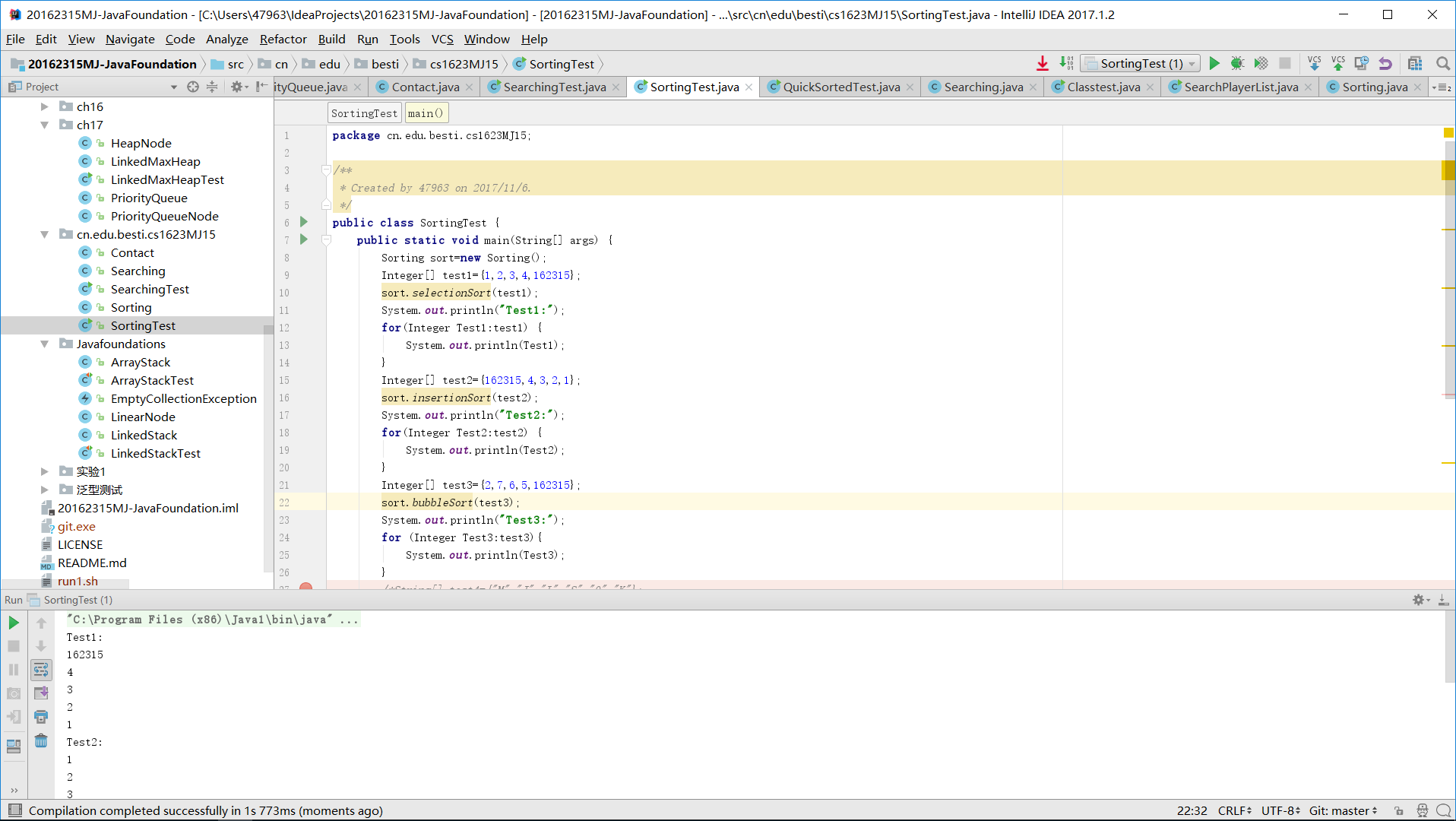
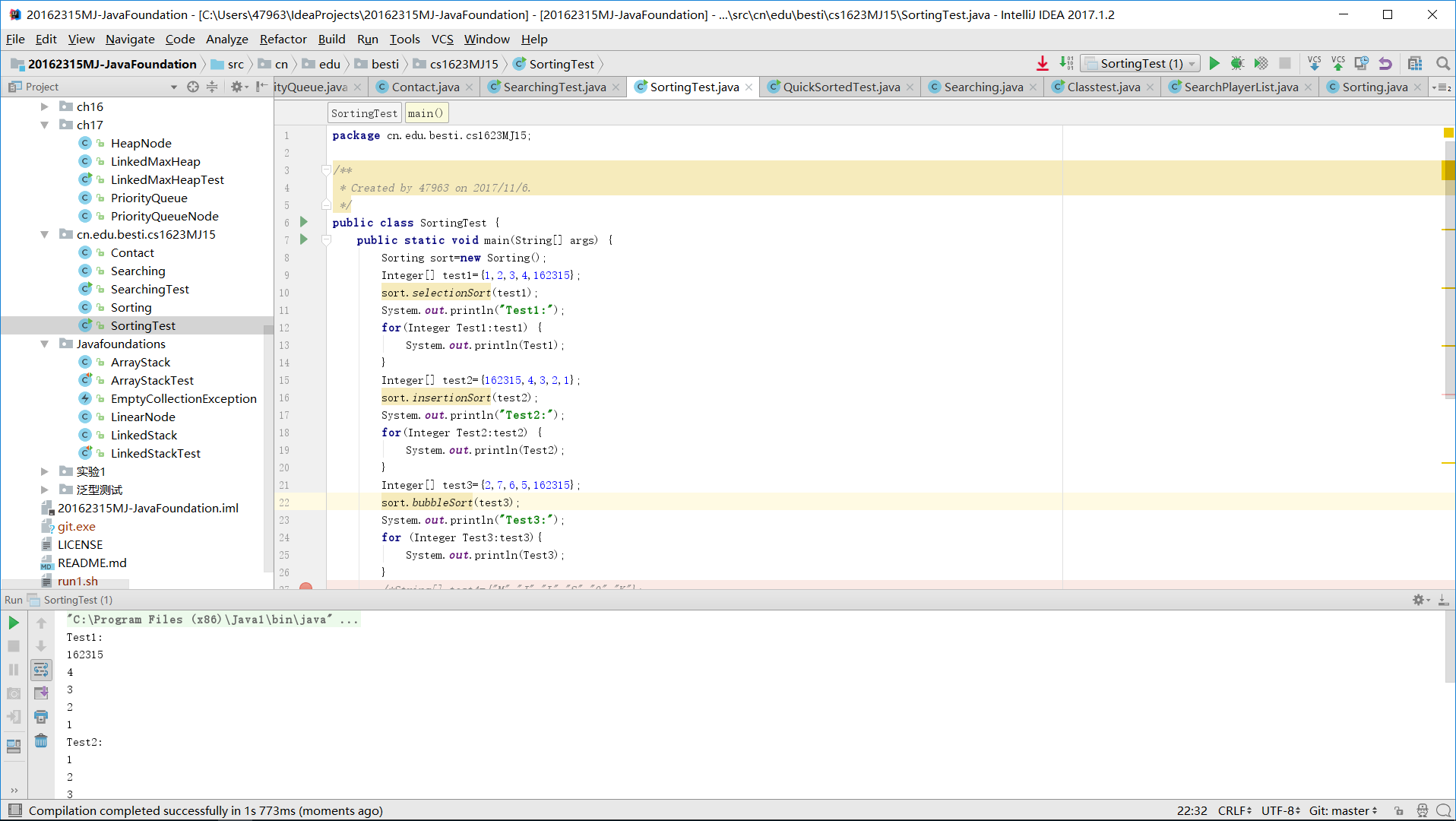
- 第二张图片:测试用例1,2分别是正序和倒序排列好的整数数组,用选择排序和插入排序测试输出正常正序结果。测试用例3是乱序整数数组,冒泡排序测试正常。
![sS4pQ.md.png]()
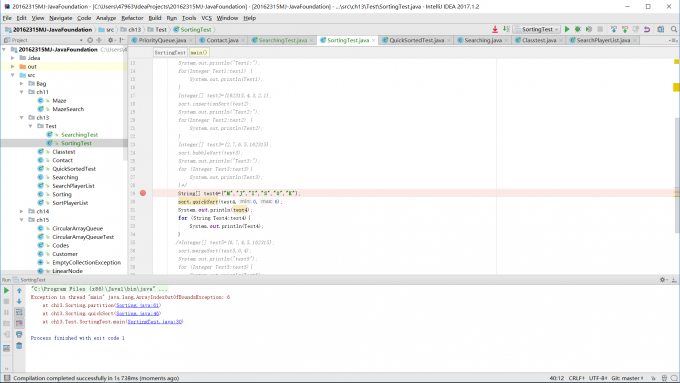
- 第三张图片:测试用例4定义了String类型数组,未实现comparable接口,无法调用campareTo方法,抛出异常;
![sS5lj.png]()
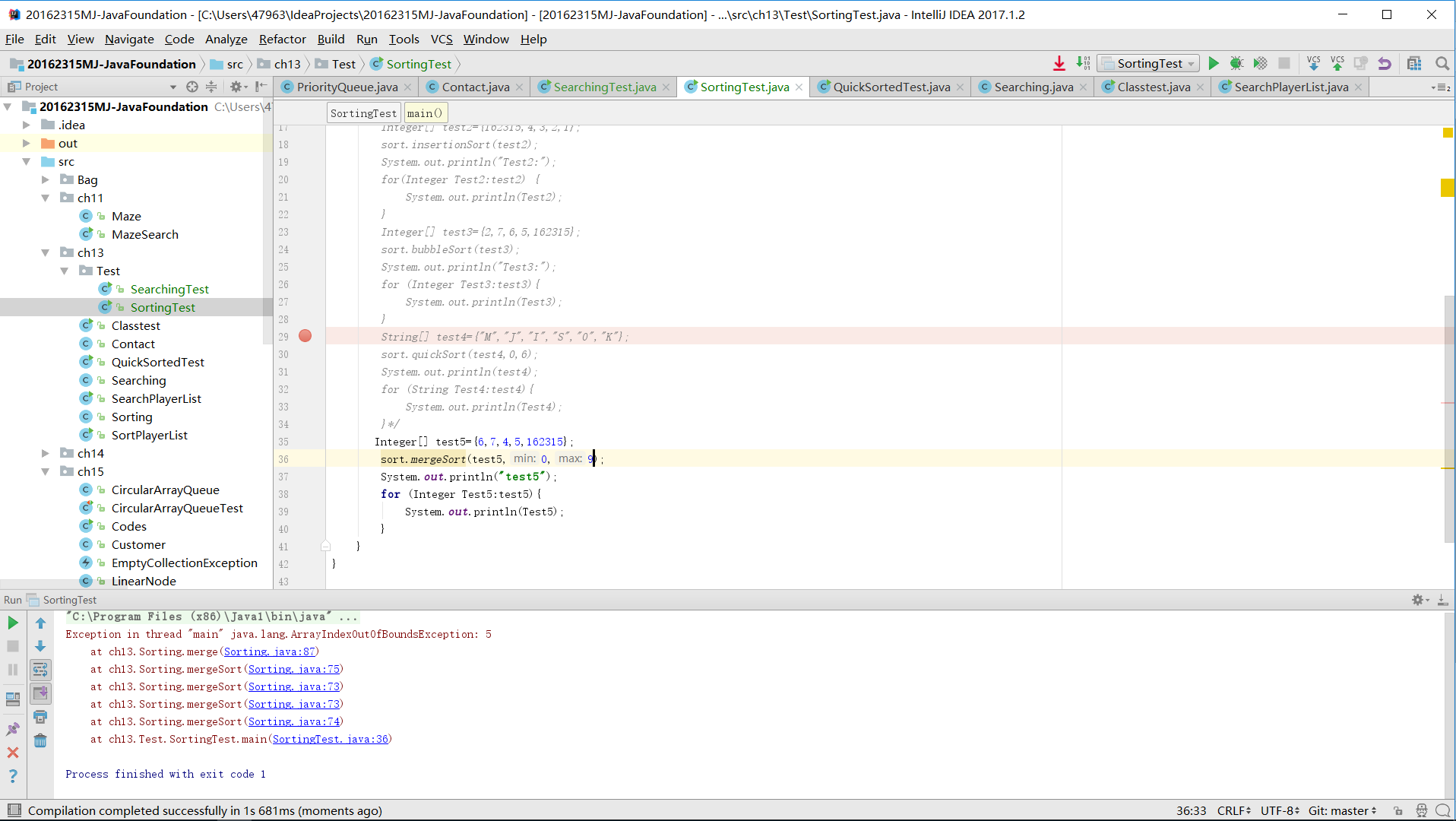
- 第四张图片:测试用例5输入的mergeSort参数超过边界抛出异常;
![sSI6s.png]()
- 第五张图片:对测试用例1selectionSort方法修改输出逆序结果。
实现过程以及收获:
- 在实现排序逆序输出时我只测试了一个算法,把选择排序算法里的capareTo方法的比较结果调成了交换后数值大的在前面先输出了。
for (int scan = index+1; scan < data.length; scan++)
if (data[scan].compareTo(data[min]) >0)
min = scan;
swap (data, min, index);
- 在本实验的实现过程中没有遇到什么困难。在查找中设计的第二个测试实例检测出了程序设计中的不足之处:当查找内容有与target相同内容的两个不同项目时,只能输出先查找到的结果,但是这样确实减少了查找的用时。在使用该方法前剔除查找条件重复项即可。
项目二
-
重构你的代码
把Sorting.java Searching.java放入 cn.edu.besti.cs1623.(姓名首字母+四位学号) 包中
把测试代码放test包中
重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种) -
![s9IZq.png]()
实现过程以及收获:
- 我在建立了要求的包之后把所有代码移了进去,调整了部分方法的import引用的位置之后就可以正常运行了,移动时IDEA自动进行了package,所以不需要我手动重新打包。
参考 http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试
提交运行结果截图
项目三
实验结果显示:
![siuRS.png]()
![siXQg.png]()
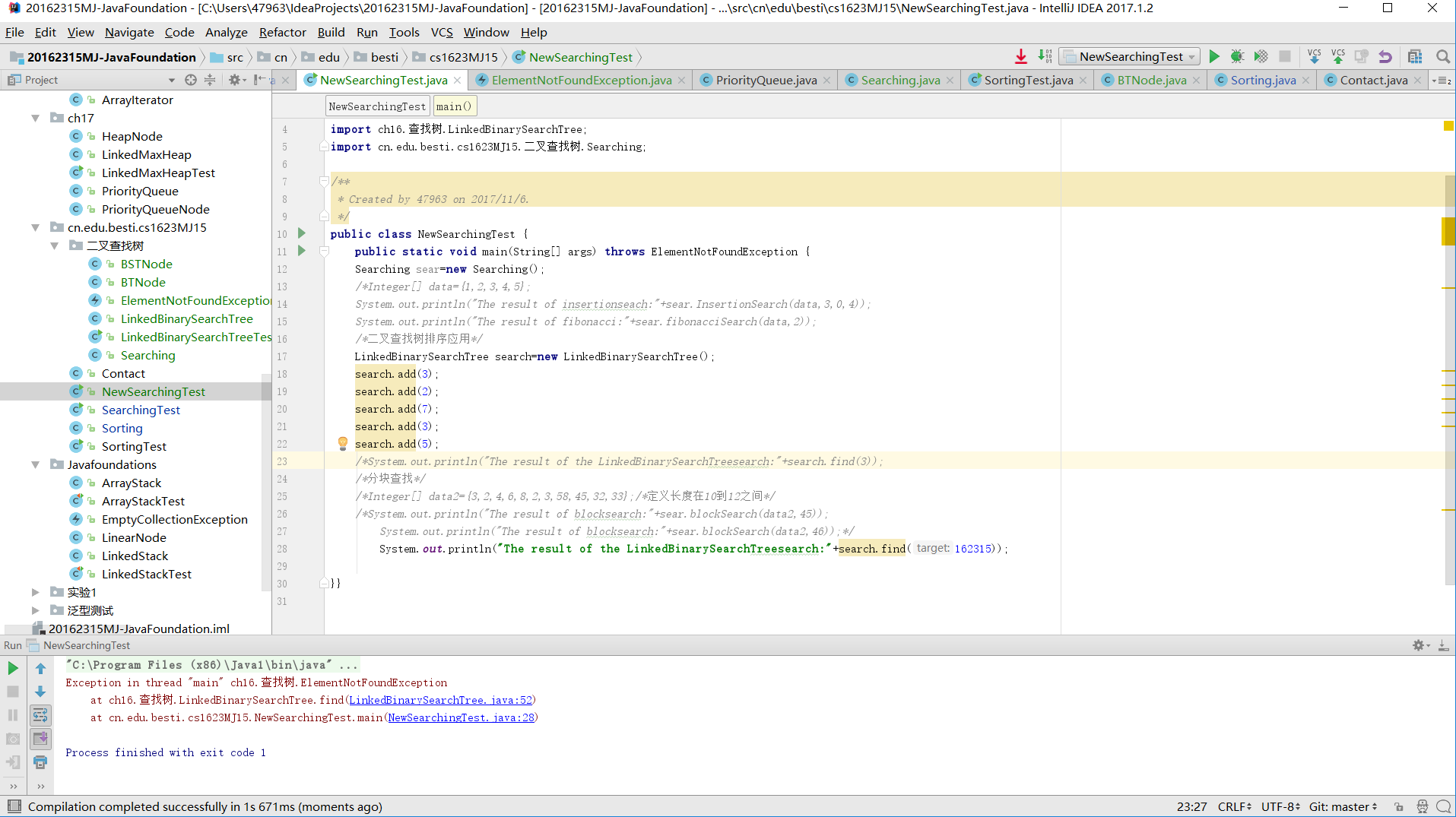
- 其他的几个查找方法在未查找目标的时候都会输出null,在二叉树查找里面我没有加入这个输出结果。所以额外加上了不在范围内的162315的查找,输出ElementNotFound异常。
实现过程以及收获:
-
插入查找我使用了参考资料里面的递归的算法,并对它进行了一定的修改,最后把输出结果也改成了输出查找项,而不是原代码中的位置。
-
最开始完全不知道斐波拉契算法查找是什么,后来读了资源博客和百度上的一些博客才知道:
斐波那契查找与折半查找很相似,他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1,即n=F(k)-1;
开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种-
1)相等,mid位置的元素即为所求
-
2)> ,low=mid+1,k-=2;说明:low=mid+1说明待查找的元素在[mid+1,hign]范围内,k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个,所以可以递归的应用斐波那契查找
-
3)< ,high=mid-1,k-=1;说明:low=mid+1说明待查找的元素在[low,mid-1]范围内,k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个,所以可以递归的应用斐波那契查找。
但是对于如何实现还是一头雾水,最后我修改了嵌入了网上的一个代码。
-
-
二叉树查找的实现较为容易,我直接调用了二叉查找树的find方法实现了。
/*调用二叉查找树的find方法*/
public int LinkedBinaryTreeSearch(Integer LinkedBinarySearchTree,Integer target) throws ElementNotFoundException {
LinkedBinarySearchTree sear=new LinkedBinarySearchTree();
Integer result= (Integer) sear.find(target);
return result;
}
-
分块查找我在网上读了一些介绍:大致总结了以下关键点:
- 1)把查找的表分为几个块(block)。
- 2)每个块内部没有明确的顺序,但是上一个块的最大元素要大(小)于下个块的最小元素。
- 3)分块查找的核心在于根据每个块的代表元素(最大(小)的元素)确定查找元素的位置,从而减小复杂度和提高效率。
- 4)在确定的块内寻找目标元素。
根据以上要点我设计了一个比较简单的分块查找算法,实现过程为:首先规定查找表的大小在10到12之间。将其排序输出分为以4为块容量划分。首先比较查找目标与块间的最大最小元素来确定元素所在的块,在在块内部直接查找得到结果。算法的核心是确定目标所在块:
for (int i=0;i<4;i++){
First[i]=data[i];
}
for (int i=0;i<4;i++){
Second[i]=data[i+4];
}
for (int i=0;i<data.length-8;i++){
Third[i]=data[i+8];
}
if (target<=First[3]){
int index=0;
while (result == null && index< First.length)
{
if (First[index]==target)
result = First[index];
index++;
}
}
if (target>=First[3]&&target<=Second[3]){
int index=0;
while (result == null && index< Second.length)
{
if (Second[index]==target)
result = Second[index];
index++;
}
}
if (target>=Second[3]&&target<=Third[Third.length-1]){
int index=0;
while (result == null && index< Third.length)
{
if (Third[index]==target)
result = Third[index];
index++;
}
}else if (target<First[0]||target>Third[Third.length-1]){
result=null;
}
如果要将它升级成一个能实现大规模查找的算法的话,块的容量要根据目标表的容量来定了。
项目四
补充实现课上讲过的排序方法:希尔排序,堆排序,桶排序,二叉树排序等
测试实现的算法(正常,异常,边界)
提交运行结果截图
推送相关代码到码云上
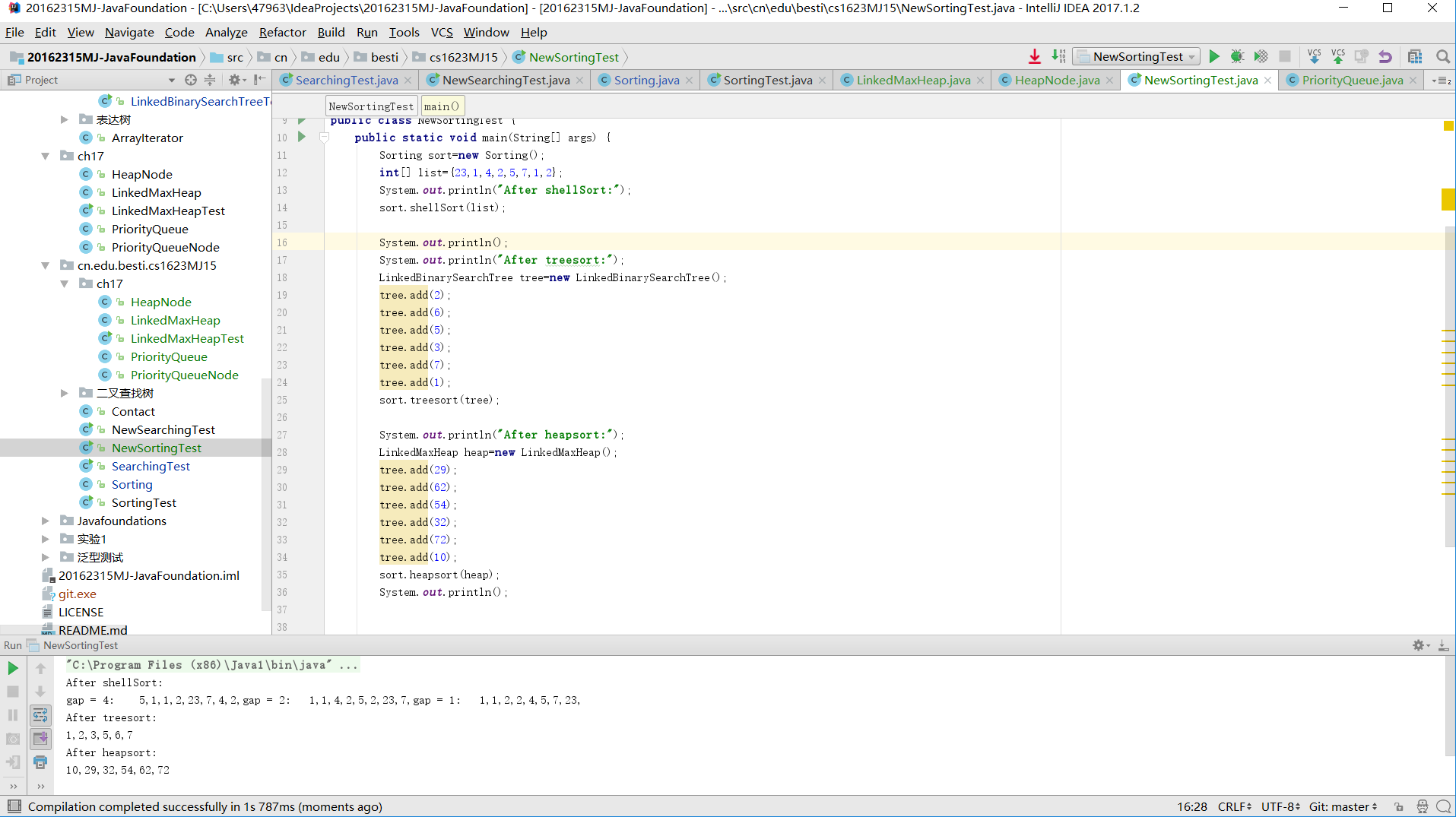
实验结果显示
实现过程以及收获
- 希尔排序跟书上给出的大多数操作都是交换算法的排序算法有点不同,它是通过比较较远间隔的元素将它们排序,然后减少比较元素的间距距离为1(相邻元素时为止)时完成排序





 浙公网安备 33010602011771号
浙公网安备 33010602011771号