第六章图(6.5-6.6.1)
6.5图的遍历
6.5.1深度优先搜索
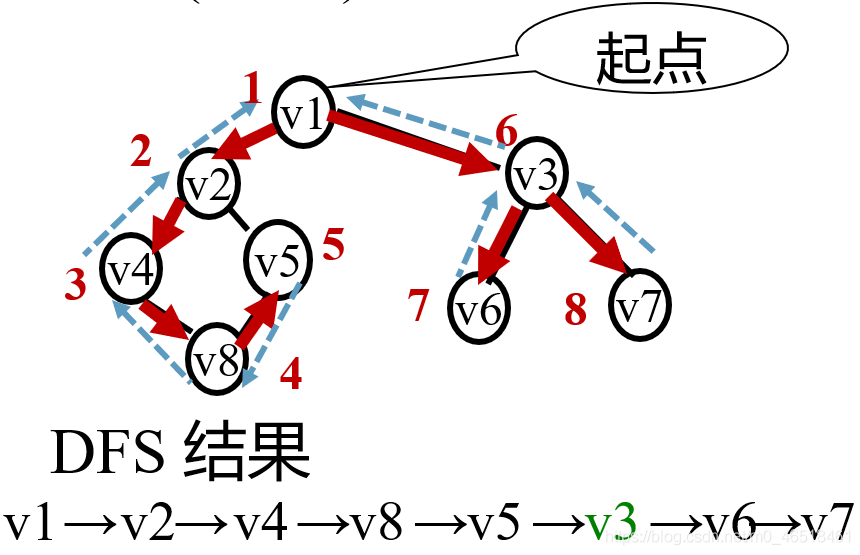
1.深度优先搜索遍历的过程
(1)从图中某个顶点v出发, 访问v。
(2)找出刚访问过的顶点的第一个未被访问的邻接点, 访问该顶点。 以该顶点为新顶点,重复此步骤, 直至刚访问过的顶点没有未被访问的邻接点为止。
(3)返回前一个访问过的且仍有未被访问的邻接点的顶点,找出该顶点的下一个未被访问的邻接点, 访问该顶点。
(4)重复步骤 (2) 和(3), 直至图中所有顶点都被访问过,搜索结束。
2.深度优先搜索遍历的算法实现
2.1 算法6.3 深度优先搜索遍历连通图
算法步骤
- 从图中某个顶点 v 出发, 访问 v, 并置 visited[v]的值为 true。
- 依次检查 v 的所有邻接点 w, 如果 visited[w]的值为 false, 再从 w 出发进行递归遍历,直到图中所有顶点都被访问过。
算法描述
bool visited [MVNum) ; //访问标志数组, 其初值为 "false"
void DFS(Graph G,int v)
{//从第 v 个顶点出发递归地深度优先遍历图G
cout<<v;visited[v)=true; //访问第 v 个顶点, 并置访问标志数组相应分扯值为 true
for(w=FirstAdjVex(G,v);w>=O;w=NextAdjVex(G,v,w))
//依次检查 v 的所有邻接点 w , FirstAdjVex (G, v)表示 v 的第一个邻接点
//NextAdjVex(G,v,w)表示 v 相对千 w 的下一个邻接点, w匀表示存在邻接点
if(!visited[w]) DFS(G,w);//对 v 的尚未访问的邻接顶点 w 递归调用 DFS
}
若是非连通图, 上述遍历过程执行之后, 图中一定还有顶点未被访间,需要从图中另选一个未被访问的顶点作为起始点 , 重复上述深度优先搜索过程, 直到图中所有顶点均被访问过为止。这样, 要实现对非连通图的遍历,需要循环调用算法 6.3, 具体实现如算法 6.4 所示。
2.2 算法6.4 深度优先搜索遍历非连通图
算法步骤
将图中每个顶点的访问标志设为false
依次(顶点编号)搜索图中每个顶点,如果未被访问,则以该顶点为起点,进行深度优先搜索遍历,否则继续检查下一个顶点,
直至图中所有顶点都被访问。
算法描述
void DFSTraverse(Graph G)
{//对非连通图G做深度优先遍历
for(v=O;v<G.vexnum;++v) visited[v]=false; //访问标志数组初始化
for(v=O;v<G.vexnum;++v) //循环调用算法6.3
if(!visited[v]) DFS(G,v); //对尚未访问的顶点调用DFS
}

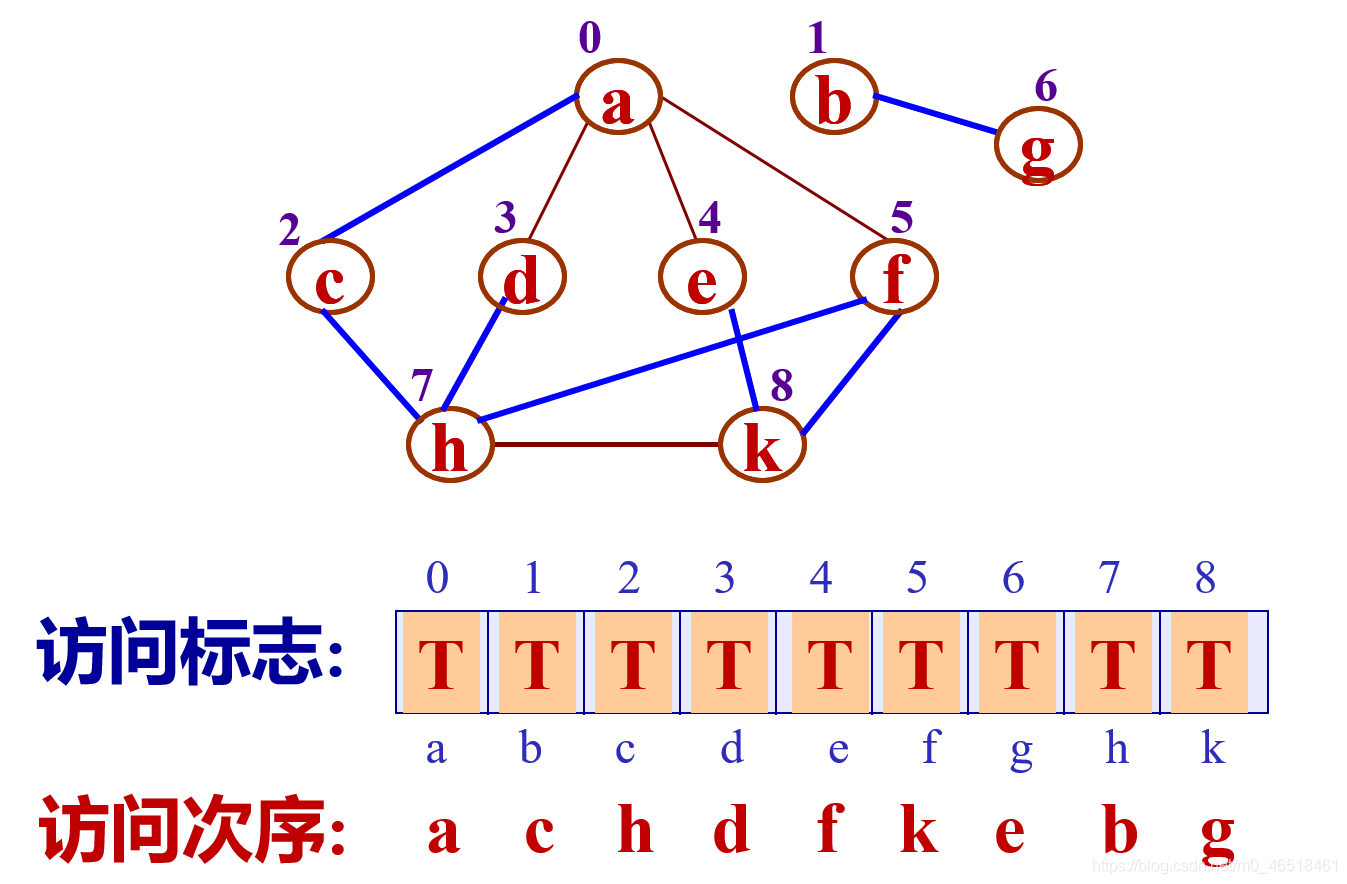
对于算法 6.4, 每调用一次算法 6.3 将遍历一个连通分量,有多少次调用,就说明图中有多少个连通分量。
在算法 6.3 中,对千查找邻接点的操作FirstAdjVex(G,v)及NextAdjVex(G,v, w)并没有具体展开。如果图的存储结构不同,这两个操作的实现方法不同,时间耗费也不同。下面的算法 6.5 、算法 6.6 分别用邻接矩阵和邻接表具体实现了算法 6.3 的功能。
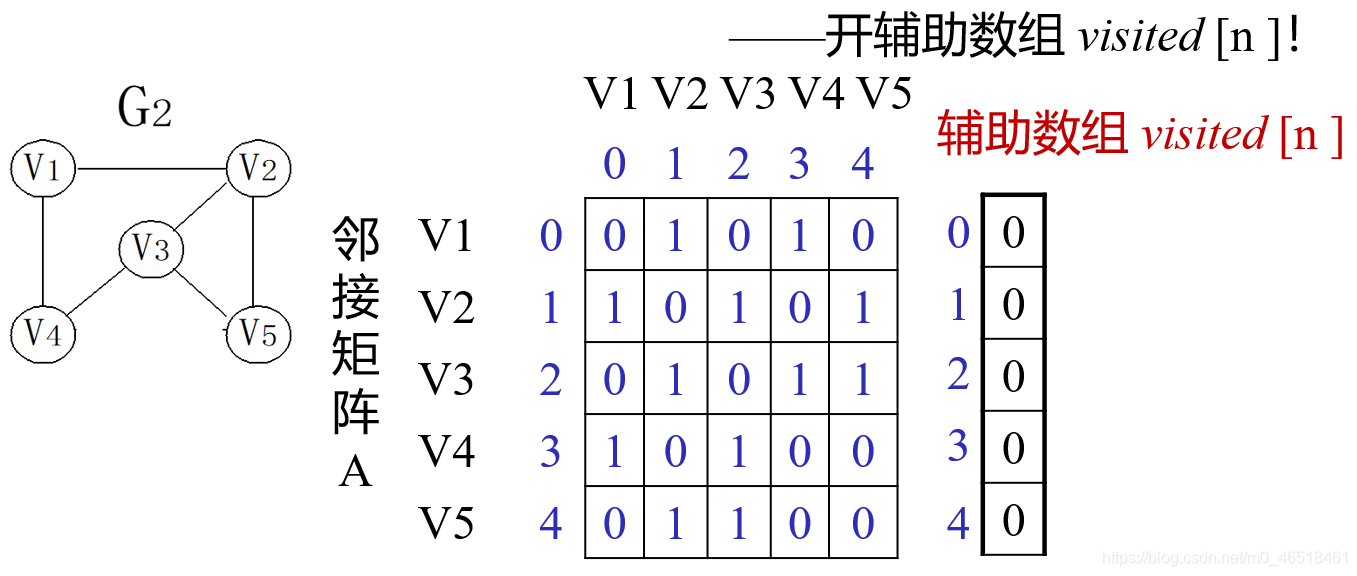
2.3 算法6.5 采用邻接矩阵表示图的深度优先搜索遍历
算法描述
void DFS_AM(AMGraph G,int v)
{//图G为邻接矩阵类型,从第v个顶点出发深度优先搜索遍历图G
cout<<v;visited[v]=true; //访问第v个顶点,并置访问标志数组相应分址值为true
for(w=O;w<G.vexnum;w++) //依次检查邻接矩阵 v所在的行
if((G.arcs[v] [w] !=O}&&(!visited[w]}} DFS(G,w};
//G.arcs[v] [w] ! =0表示w是v的邻接点, 如果w未访问, 则递归调用DFS
}
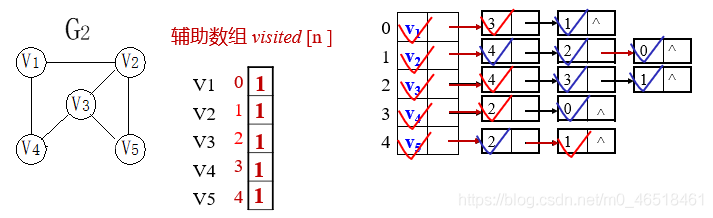
2.4 算法6.6采用邻接表示图的深度优先搜索遍历
算法描述
void DFS_AL (ALGraph G,int v)
{//图G为邻接表类型, 从第v个顶点出发深度优先搜索遍历图G
cout<<v;visited[v]=true; //访问第v个顶点,并置访问标志数组相应分量值为true
p=G.vertices[v] .firstarc; //p指向v的边链表的第一个边结点
while(p!=NULL) //边结点非空
{
w=p->adjvex;//表示w是v的邻接点
if(!visited[w]) DFS(G,w); //如果口未访问, 则递归调用DFS
p=p->nextarc; //p指向下一个边结点
}//while
}
3.深度优先搜索遍历的算法分析
分析上述算法,在遍历图时,对图中每个顶点至多调用一次 DFS 函数,因为一旦某个顶点被标志成巳被访问,就不再从它出发进行搜索。 因此,遍历图的过程实质上是对每个顶点查找其邻接点的过程,其耗费的时间则取决千所采用的存储结构。 当用邻接矩阵表示图时,查找每个顶点的邻接点的时间复杂度为 O(n2 ), 其中 n为图中顶点数。而当以邻接表做图的存储结构时,查找邻接点的时间复杂度为O(e), 其中e为图中边数。由此, 当以邻接表做存储结构时,深度优先搜索遍历图的时间复杂度为 O(n + e)。
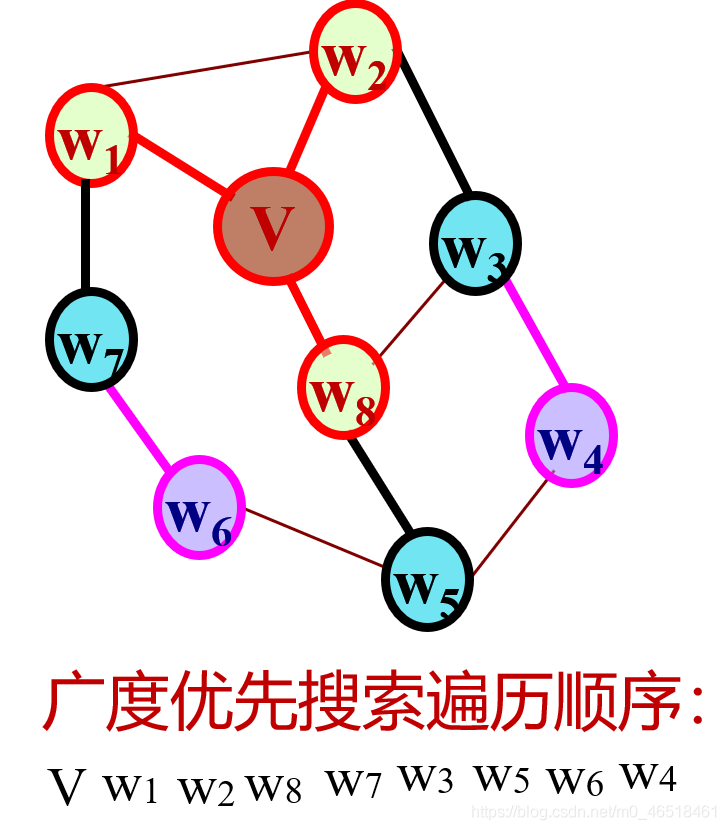
6.5.2广度优先搜索
1.广度优先搜索遍历的过程
- 从图中某个顶点v出发,访问v。
- 依次访问v的各个未曾访问过的邻接点。
- 分别从这些邻接点出发依次访问它们的邻接点, 并使 “先被访问的顶点的邻接点“ 先千”后被访问的顶点的邻接点” 被访问。重复步骤(3), 直至图中所有已被访问的顶点的邻接点都被访间到
2.广度优先搜索遍历的算法实现
2.1 算法6.7 广度优先搜索遍历连通图
算法步骤
- 从图中某个顶点 v 出发, 访问 v, 并置 visited[v]的值为 true, 然后将 v 进队。
- 只要队列不空, 则重复下述操作:
- 队头顶点 u 出队;
- 依次检查 u 的所有邻接点 w, 如果 visited[w]的值为 false, 则访问 w, 并置 visited[w]的值为 true, 然后将 w 进队。
算法描述
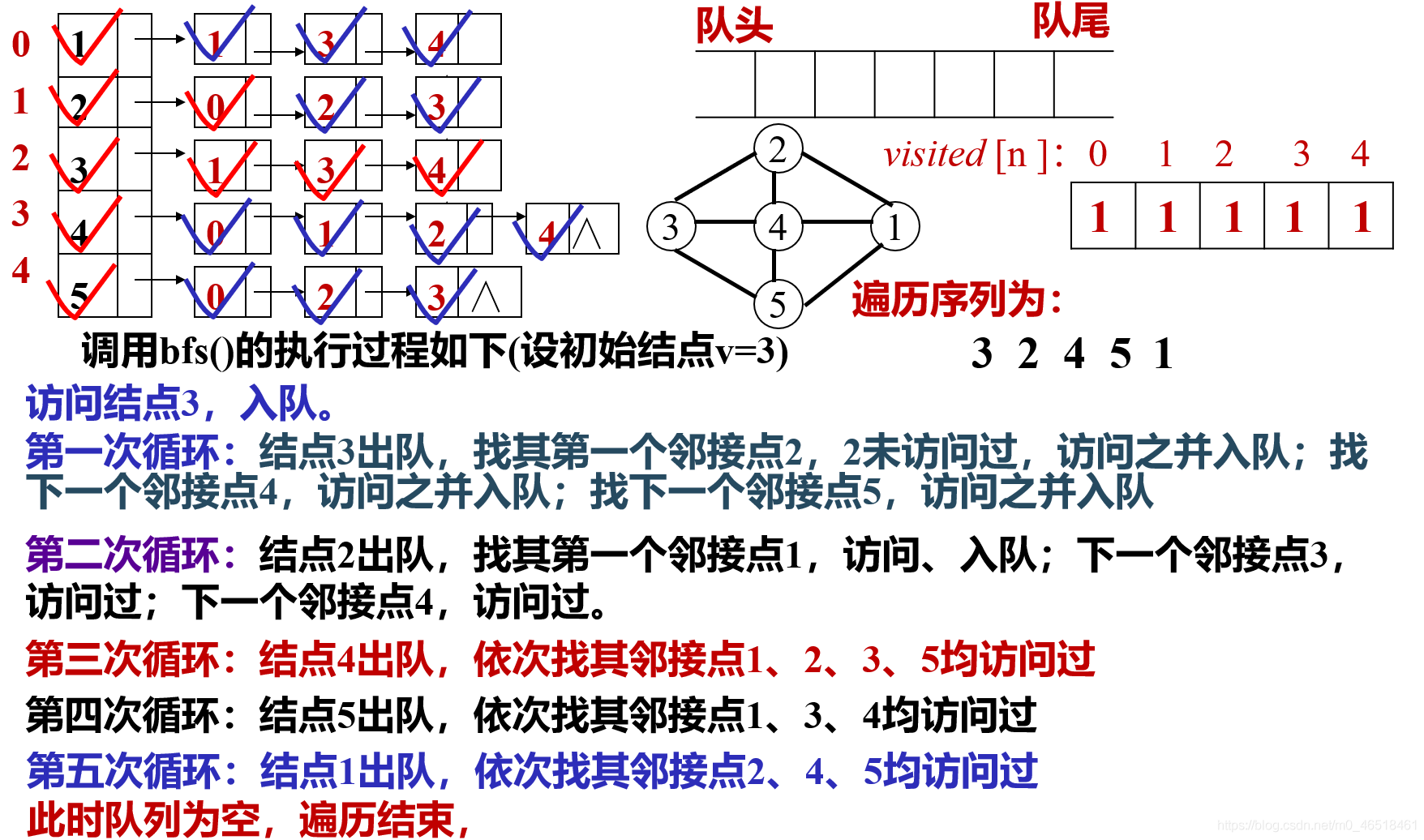
void BFS{Graph G,int v)
{//按广度优先非递归遍历连通图G
COUt<<v;visited[v]=true;//访问第v个顶点,并置访问标志数组相应分址值为true
InitQueue(Q);//辅助队列Q初始化, 置空
EnQueue(Q,v);//v进队
while (! QueueEmpty (Q))//队列非空
{
DeQueue (Q, u);/ /队头元素出队并置为u
for(w=FirstAdjVex(G,u);w>=O;w=NextAdjVex(G,u,w))
//依次检查u的所有邻接点w, FirstAdjVex(G,u)表示u的第一个邻接点
//NextAdjVex(G,u,w)表示u相对于w的下一个邻接点,w;;,.o表示存在邻接点
if (!visited [w])/ /w为u的尚未访问的邻接顶点
{
cout<<w; visited[w]=true; //访问 w, 并置访问标志数组相应分扯值为true
EnQueue (Q, w) ; //w进队
}
}
}
若是非连通图,上述遍历过程执行之后,图中一定还有顶点未被访问,需要从图中另选一个未被访问的顶点作为起始点,重复上述广度优先搜索过程,直到图中所有顶点均被访问过为止。
对于非连通图的遍历,实现算法类似于算法6.4, 仅需将原算法中的DFS函数调用改为BFS函数调用
3.广度优先搜索遍历的算法实现
分析上述算法,每个顶点至多进一次队列。遍历图的过程实质上是通过边找邻接点的过程,因此广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同,即当用邻接矩阵存储时,时间复杂度为O(n2 ); 用邻接表存储时,时间复杂度为O(n+ e)。两种遍历方法的不同之处仅仅在于对顶点访问的顺序不同。
6.6图的应用
6.6.1最小生成树
1.普里姆算法
1.1普里姆算法的构造过程
1.2普里姆算法的实现

//辅助数组的定义,用来记录从顶点集 u到v-u 的权值最小的边
struct
{
VerTexType adjvex; //最小边在U中的那个顶点
ArcType lowcost; //最小边上的权值
} closedge [MVNum];
算法6.8 普里姆算法
算法步骤
- 首先将初始顶点 u加入U中,对其余的每一个顶点 VJ, 将closedge[J]均初始化为到 u 的边信息。
- 循环 n - I 次, 做如下处理:
• 从各组边 closedge 中选出最小边 closedge[k], 输出此边;
• 将K加入U中;
• 更新剩余的每组最小边信息 closedge[j], 对于 v-u中的边, 新增加了一条从 K 到j 的边, 如果新边的权值比 closed ge[i].lowcost 小,则将 closedge[j].lowcost 更新为新边的权值
算法描述
void MiniSpanTree_Prim(AMGraph G,VerTexType u)
{//无向网G以邻接矩阵形式存储, 从顶点u出发构造G的最小生成树T, 输出T的各条边
k=LocateVex(G,u); //k为顶点 u 的下标
for(j=O;j<G.vexnum;++j) //对v-u 的每一个顶点 Vj, 初始化 closedge[j]
if(j!=k) closedge[j]={u,G.arcs[k][j]}; //{adjvex, lowcost}
closedge[k].lowcost=O; //初始, U={u}
for(i=l;i<G.vexnum;++i)
{//选择其余 n-1 个顶点,生成 n-1 条边(n=G.vexnum)
k=Min(closedge);
//求出 T 的下一个结点:第 K 个顶点, closedge[k]中存有当前最小边
uO=closedge[k] .adjvex; //u0为最小边的一个顶点,u0属于U
vO=G.vexs[k]; //vO 为最小边的另一个顶点, v0属于V-U
cout<<uO<<vO; //输出当前的最小边(uO, vO)
closedge[k] .lowcost=O;//第k个顶点并入u集
for(j=O;j<G.vexnum;++j)
if(G.arcs[k] [j]<closedge[j] .lowcost) //新顶点并入u 后重新选择最小边
closedge [j]={G.vexs [kl ,G.arcs [kl [j]};
}
}
2.克鲁斯卡尔算法
2.1克鲁斯卡尔算法的构造过程

2.2克鲁斯卡尔算法的实现

算法6.9 克鲁斯卡尔算法
算法步骤

算法描述
void MiniSpanTree_ Kruskal(AMGraph G)
{//无向网G以邻接矩阵形式存储,构造G的最小生成树T, 输出T的各条边
Sort (Edge); //将数组 Edge 中的元素按权值从小到大排序
for(i=O;i<G.vexnum;++i) //辅助数组,表示各顶点自成一个连通分址
Vexset[i]=i;
for(i=O;i<G.arcnum;++i) //依次查看数组 Edge 中的边
{
vl=LocateVex(G,Edge[i] .Head); //vl 为边的始点 Head 的下标
v2=LocateVex(G,Edge[i] .Tail); //v2 为边的终点 Ta过的下标
vsl=Vexset[vl]; //获取边 Edge[i]的始点所在的连通分址 vsl
vs2=Vexset[v2]; //获取边 Edge[i]的终点所在的连通分扯 vs2
if(vsl!=vs2) //边的两个顶点分属不同的连通分量
{
cout«Edge[i] .Head «Edge[i] .Tail;//输出此边
for(j=O;j<G.vexnurn;++j) //合并 VS1 和 VS2 两个分益, 即两个集合统一编号
if(Vexset[ j] ==vs2) Vexset [ j] =vsl; / /集合编号为 vs2 的都改为 vsl
}
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号