20200509 自招题目
-
对集合 \(\{1,2,\cdots,n\}\) 及其每一个非空子集,定义一个唯一确定的"交替和"如下:按照递减的次序重新排列该子集,然后交替地减或加后继的数所得的结果,例如,集合 \(\{1,2,4,6,9\}\) 的"交替和"是 \(9-6+4-2+1=6\) ,\(\{5,6\}\) 的"交替和"是 \(6-5=1\) ,\(\{2\}\) 的"交替和"是 \(2\) .那么,对于 \(n=7\) ,求所有子集的"交替和"的总和.
- 解:设 \(\forall A\subseteq\{1,2,\cdots,n\}\) ,\(A\) 的"交替和"为 \(f(A)\) ,集合 \(\{1,2,\cdots,x\}\) 的所有子集的"交替和"的总和为 \(g(x)\),
易得 \(\forall A\subseteq\{1,2,\cdots,x-1\},f(A\cup\{x\})=x-f(A)\),
又集合 \(\{1,2,\cdots,x-1\}\) 共有 \(2^{x-1}\) 个子集,集合 \(\{1,2,\cdots,x\}\) 的所有子集都为 \(\{1,2,\cdots,x-1\}\) 的子集或子集与 \(\{x\}\) 的并,
\(\therefore\) 集合 \(\{1,2,\cdots,x-1\}\) 的所有子集与 \({x}\) 的并的"交替和"的总和为\[\sum\limits_{i=1}^{2^{x-1}}(x-f(A_i))=2^{x-1}x-g(x-1), \quad(A_i\ \text{为集合}\ \{1,2,\cdots,x-1\}\ \text{的第}\ i\ \text{个子集}) \]\(\therefore\) \(g(x)=g(x-1)+[2^{x-1}x-g(x-1)]=2^{x-1}x\),
\(\therefore\) 对于 \(n=7\),所有子集的"交替和"的总和为
\[g(7)=2^{7-1}\times7=448. \] - 解:设 \(\forall A\subseteq\{1,2,\cdots,n\}\) ,\(A\) 的"交替和"为 \(f(A)\) ,集合 \(\{1,2,\cdots,x\}\) 的所有子集的"交替和"的总和为 \(g(x)\),
-
\(n\) 元集合具有多少个不同的不交子集对?
-
解:设 \(A_i=\{x_1,x_2,\cdots,x_i\}(i=1,2,\cdots,n)\),且 \(A_i\) 的不交子集对组成的集合为 \(B_i\).
-
若不交子集对为有序集合对,则
\[\forall(S,T)\in B_{i-1}(i=1,2,\cdots,n),(S,T),(S\cup\{x_i\},T),(S,T\cup\{x_i\})\in B_i, \]且不存在其他集合对属于 \(B_i\),
\(\therefore\) \(\operatorname{card}(B_i)=3\operatorname{card}(B_{i-1})\),
又 \(\operatorname{card}(B_0)=1\),
\(\therefore\) \(\operatorname{card}(B_i)=3^i\),
\(\therefore\) \(n\) 元集合具有的不交子集对的个数为
\[\operatorname{card}(B_n)=3^n. \] -
若不交子集对为无序集合对,则
\[\forall(S,T)\in \complement_{B_{i-1}}(\empty,\empty)(i=1,2,\cdots,n),(\empty,\{x_i\}),(S,T),(S\cup\{x_i\},T),(S,T\cup\{x_i\})\in B_i, \]且不存在其他集合对属于 \(B_i\),
\(\therefore\) \(\operatorname{card}(B_i)-1=3[\operatorname{card}(B_{i-1})-1]+1\Leftrightarrow \operatorname{card}(B_i)=3\operatorname{card}(B_{i-1})-1\),
又 \(\operatorname{card}(B_0)=1\),
\(\therefore\) \(\operatorname{card}(B_i)=\sum\limits_{j=0}^{i-1}3^j+1=\frac{3^{i-1}-1}2+1=\frac{3^{i-1}+1}2\),
\(\therefore\) \(n\) 元集合具有的不交子集对的个数为
\[\operatorname{card}(B_n)=\frac{3^{n-1}+1}2. \]
-
-
-
通信工程常用 \(n\) 元数组 \((a_1,a_2,\cdots,a_n)\) 表示信息,其中 \(a_i=0\) 或 \(1,i,n\in \mathbb N\) .设 \(u=(a_1,a_2,\cdots,a_n),v=(b_1,b_2,\cdots,b_n)\) ,\(d(u,v)\) 表示 \(u\) 和 \(v\) 中相对应的元素不同的个数.
(1) \(u=(0,0,0,0,0)\) ,问存在多少个 \(5\) 元数组 \(v\) 使得 \(d(u,v)=1\);
-
解:由题意可知 \(d(u,v)\) 为 \(v\) 中 \(1\) 的个数,
\(\therefore\) 存在使 \(d(u,v)=1\) 的 \(5\) 元数组 \(v\) 的个数为
\[\mathrm C_5^1=5. \]
(2) \(u=(1,1,1,1,1)\) ,问存在多少个 \(5\) 元数组 \(v\) 使得 \(d(u,v)=3\);
-
解:由题意可知 \(d(u,v)\) 为 \(v\) 中 \(0\) 的个数,
\(\therefore\) 存在使 \(d(u,v)=3\) 的 \(5\) 元数组 \(v\) 的个数为
\[\mathrm C_5^3=10. \]
(3) 令 \(w=(\underbrace{0,0,\cdots,0}_{n\text{个}0}),u=(a_1,a_2,\cdots,a_n),v=(b_1,b_2,\cdots,b_n)\) ,求证:\(d(u,w)+d(v,w)\ge d(u,v)\).
-
证明:由题意可知 \(d(u,w)\) 为 \(u\) 中 \(1\) 的个数, \(d(v,w)\) 为 \(v\) 中 \(1\) 的个数.
当 \(u\) 与 \(v\) 中不存在都为 \(1\) 的相对应的元素时,\(d(u,w)+d(v,w)=d(u,v)\);
当 \(u\) 与 \(v\) 中存在都为 \(1\) 的相对应的元素时,\(d(u,w)+d(v,w)>d(u,v)\).
综上,\(d(u,w)+d(v,w)\ge d(u,v)\).
-
-
已知 \(x_i>0(i=1,2,\cdots,n),\prod\limits_{i=1}^n x_i=1\) ,求证:\(\prod\limits_{i=1}^n(\sqrt 2+x_i)\ge(\sqrt 2+1)^n\).
-
法一:设 \(n=k\in\mathbb N^+\).
\(\mathrm{(i)}\) 当 \(k=1\) 时,条件显然成立.
\(\mathrm{(ii)}\) 当 \(k\ge 2\) 时,假设当 \(n=k-1\) 时条件成立,不妨设 \(x_{k-1}\le 1,x_k\ge 1\),则
\[\begin{aligned} (x_{k-1}-1)(x_k-1) &\le 0\\ x_{k-1}x_k-x_{k-1}-x_k+1 &\le 0\\ x_{k-1}+x_k &\ge 1+x_{k-1}x_k\\ 2+\sqrt 2(x_{k-1}+x_k)+x_{k-1}x_k &\ge 2+\sqrt 2(1+x_{k-1}x_k)+x_{k-1}x_k\\ (\sqrt 2+x_{k-1})(\sqrt 2+x_k) &\ge (\sqrt 2+1)(\sqrt 2+x_{k-1}x_k)\\ \frac{(\sqrt 2+x_{k-1})(\sqrt 2+x_k)} {\sqrt 2+x_{k-1}x_k} &\ge \sqrt 2+1, \end{aligned} \]\(\therefore\)
\[\begin{aligned} (\sqrt 2+x_1)(\sqrt 2+x_2)\cdots(\sqrt 2+x_{k-1}x_k) &\ge(\sqrt 2+1)^{k-1}\\ (\sqrt 2+x_1)(\sqrt 2+x_2)\cdots(\sqrt 2+x_{k-1}x_k) \cdot \frac{(\sqrt 2+x_{k-1})(\sqrt 2+x_k)} {\sqrt 2+x_{k-1}x_k} =\prod_{i=1}^k(\sqrt 2+x_i) &\ge(\sqrt 2+1)^k, \end{aligned} \]得证.
-
法二:由柯西不等式可得
\[(\sqrt 2+x_i)(\sqrt 2+x_j) \ge(\sqrt 2+\sqrt{x_ix_j}), \quad(i,j=1,2,\cdots,n) \]当且仅当 \(\sqrt 2x_j=\sqrt 2x_i\),即 \(x_i=x_j\) 时,该式去等号,
\(\therefore\) 在 \(x_ix_j\) 不变的前提下,总能将 \(x_i,x_j\) 调整到相等,使得 \((\sqrt 2+x_i)(\sqrt 2+x_j)\) 变小.
记
\[S=\prod\limits_{i=1}^n(\sqrt 2+x_i), \]则 \(S\) 取最小值时,所有 \(x_i\) 都相等,否则总可以调整使 \(S\) 更小,
\(\therefore\) \(S\) 的最小值为 \(\prod\limits_{i=1}^n(\sqrt 2+1)=(\sqrt 2+1)^n\),即证.
-
法三:设 \(A_i\) 为 \(\prod\limits_{i=1}^n(\sqrt 2+x_i)\) 展开后含 \((\sqrt 2)^{n-i}\) 的项的和,\(B_i\) 为 \((\sqrt 2+1)^n\) 展开后含 \((\sqrt 2)^{n-i}\) 的项的和,则
\[ \begin{aligned} \prod\limits_{i=1}^n (\sqrt 2+x_i) &=\sum\limits_{i=0}^n A_i,\\ (\sqrt 2+1)^n &=\sum\limits_{i=0}^n B_i, \end{aligned} \]易知
\[\begin{aligned} &A_i=(\sqrt 2)^{n-i}( \underbrace{ \overbrace{ x_1x_2\cdots x_i }^{\text{共}~i~\text{个}} +\cdots }_{\text{共}~\mathrm C_n^i~\text{项}}),\\ &B_i=(\sqrt 2)^{n-i} \mathrm C_n^i, \end{aligned} \]又由 \(AM\text-GM\) 不等式得
\[\frac{A_i}{B_i} =\frac 1{\mathrm C_n^i} (\underbrace{ \overbrace{ x_1x_2\cdots x_i }^{\text{共}~i~\text{个}} +\cdots }_{\text{共}~\mathrm C_n^i~\text{项}}) \ge\sqrt[\mathrm C_n^i] {\underbrace{ (\overbrace{ x_1x_2\cdots x_i }^{\text{共}~i~\text{个}} )\times\cdots }_{\text{共}~\mathrm C_n^i~\text{项}}} =1, \]\(\therefore\) \(A_i\ge B_i\),
\(\therefore\) \(\prod\limits_{i=1}^n(\sqrt 2+x_i)\ge(\sqrt 2+1)^n\).
-
-
已知实系数二次函数 \(f(x)\) 与 \(g(x)\),\(f(x)=g(x)\) 和 \(3f(x)+g(x)=0\) 有两重根,\(f(x)=0\) 有两相异实根,求证:\(g(x)=0\) 没有实根.
-
证明:假设 \(g(x)=0\) 有实根,
不妨设
\[f(x)=a_1(x-b_1)(x-c_1),\quad(a_1>0,b_1\le c_1)\\ g(x)=a_2(x-b_2)(x-c_2),\quad(a_2\not=0,b_2\le c_2) \]又有 \(f(x)=g(x),3f(x)+g(x)=0\Leftrightarrow -3f(x)=g(x)\) 有两重根,
即函数 \(y=g(x)\) 的图像与 \(y=f(x),y=-3f(x)\) 各有且只有一个公共点,且 \(a_1\not=a_2,-3a_1\not=a_2\).
易知函数 \(y=f(x)\) 和 \(y=-3f(x)\) 的图像都交 \(x\) 轴于点 \((b_1,0),(c_1,0)\),\(y=g(x)\) 的图像交 \(x\) 轴于点 \((b_2,0),(c_2,0)\),
则可得下图:
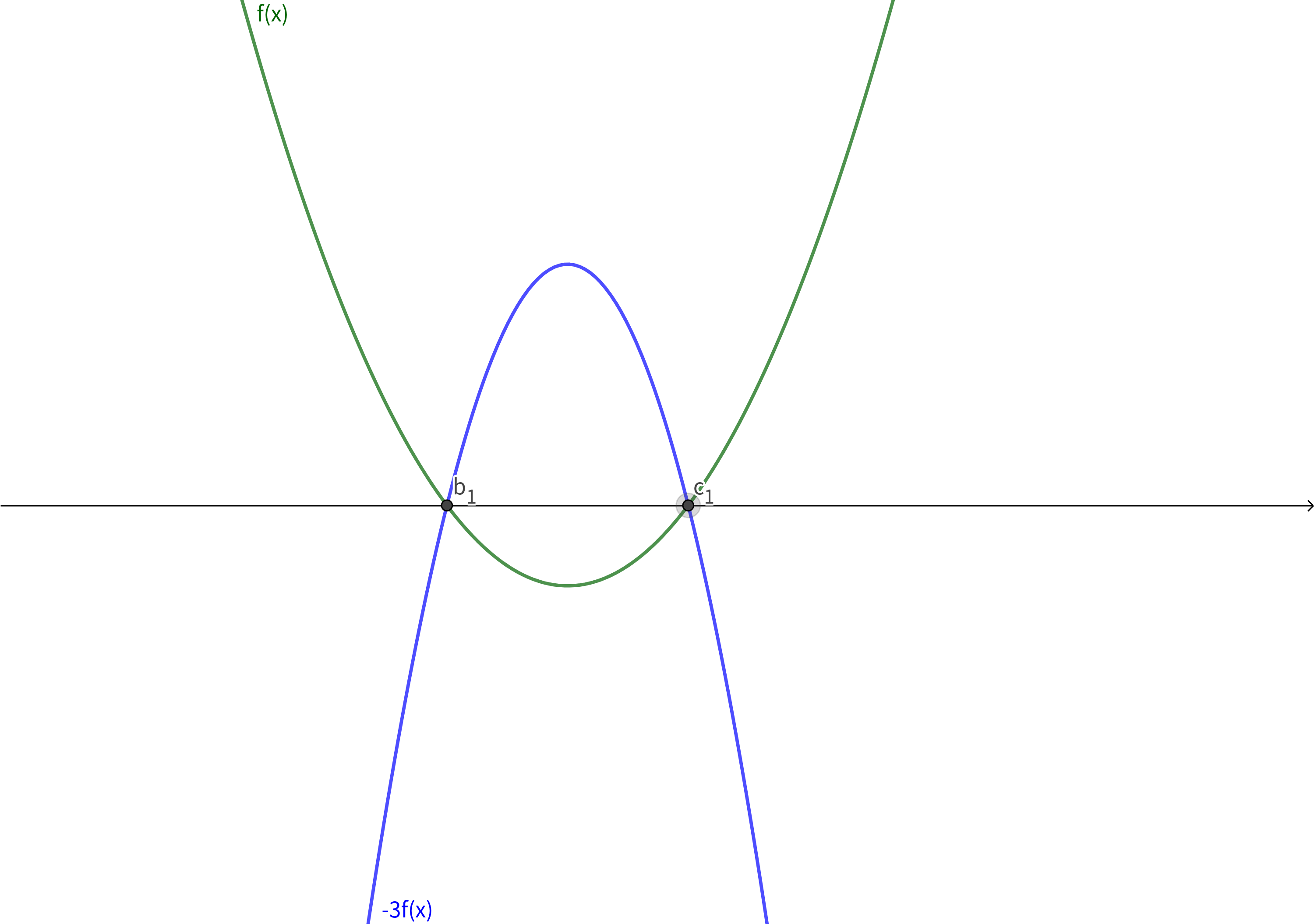
-
当 \(b_2\ge b_1\) 且 \(c_2\le c_1\) 时,显然不符题意;
-
当 \(b_2<b_1\) 且 \(c_2>c_1\) 时,显然不符题意;
-
当 \(c_2\le b_1\) 或 \(b_2\ge c_1\) 时,由于 \(a_1\not=a_2\) 且 \(-3a_1\not=a_2\),
即 \(f''(x)\not=g''(x)\) 且 \([-3f(x)]''\not=g''(x)\),
\(\therefore\) 函数 \(g(x)\) 的图像与 \(f(x)\) 或 \(-3f(x)\) 图像至少有两个交点,不符题意.
综上,\(g(x)=0\) 有实根不符题意,
即 \(g(x)=0\) 没有实根.
-
-
我太弱了!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号