模型评估与选择

• 获得测试结果: 评估方法.
• 评估性能优劣: 性能度量.
• 判断实质差别: 比较检验.

〇. 经验误差与过拟合

• 泛化误差: 未来样本上的误差; 训练误差: 也称作经验误差;

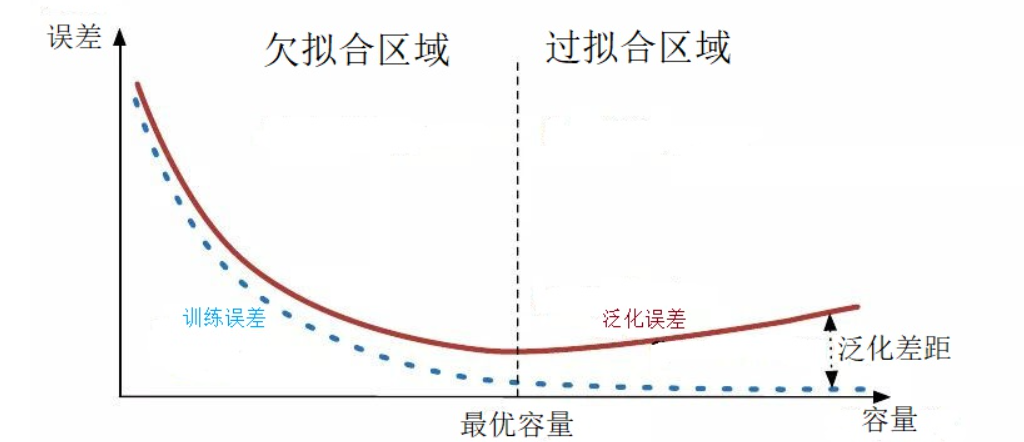
• 过拟合(经验误差小, 泛化误差大); 欠拟合(经验误差大).

一. 评估方法

包含 \(m\) 个样本的数据集 \(D\), 既要训练又要测试, 如何划分? - 数据集划分.

1.1 留出法 (hold-out)

• 做法: 直接将数据集划分为两个互斥集合: 训练集 \(S\), 测试集 \(T\).
• 注意: \(S\) 和 \(T\) 的划分要尽可能保持数据分布一致性.
  • 分层抽样: 保持类别比例一致.
  • 若干次随机抽样, 取平均值.
• 比例: \(S/T\) 比例通常在 2:1 ~ 4:1.

1.2 交叉验证法 (cross-validation)

• 将数据集划分为 \(k\) 个大小相似的互斥子集(分层采样);
• 每次选 \(1\) 个子集作为测试集, 余下的为训练集;
• 最终取 \(k\) 个测试结果的均值.

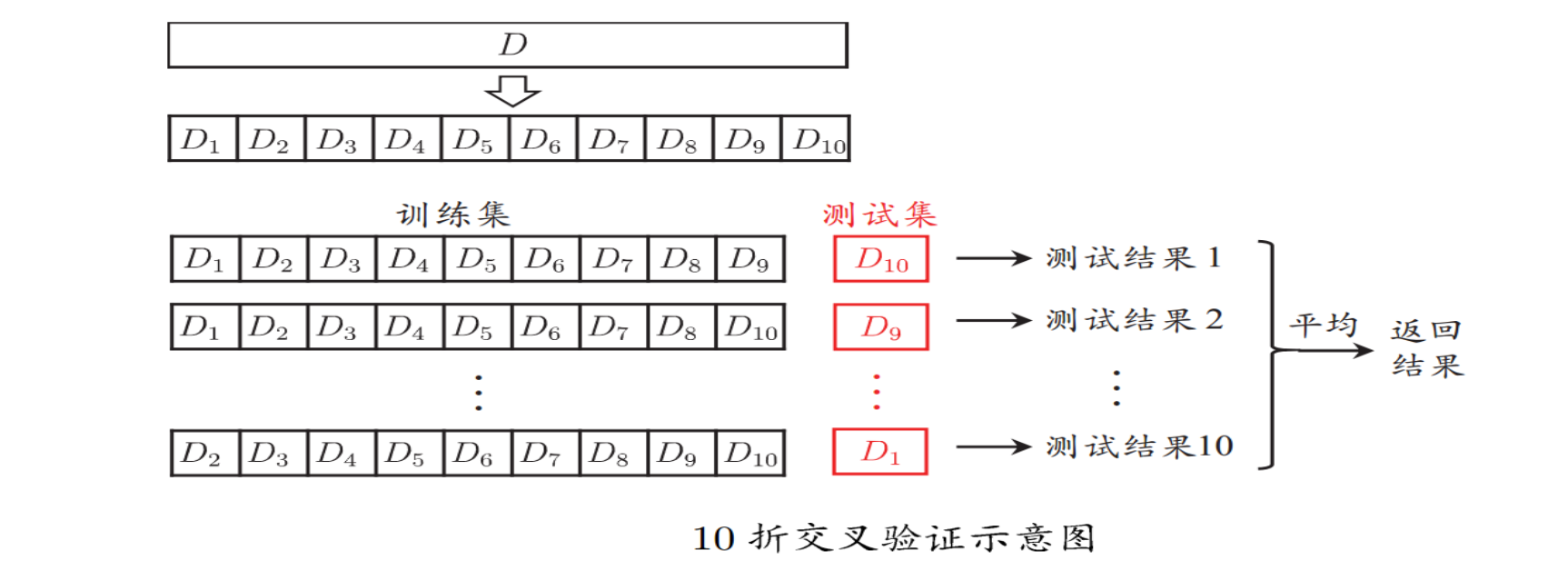
• \(10\) 次 \(10\) 折交叉验证, 含义:
  • 将 \(D\) 划分为 \(k\) 个子集可能有多种划分方式, 随机使用不同的划分方式 \(p\) 次.
  • 最终结果为 \(p\) 次 \(k\) 折交叉验证, 是所有测试结果的均值.
• 留一法: 数据集 \(D\) 包含 \(m\) 个样本时, 取 \(k=m\).
  • 此时每个样本都被测试, 不受随机取样的影响.
  • 通常, 结果更加准确, 而计算开销太大.

二. 性能度量, performance measurement

根据测试结果 \(f(x_i)\) 和样本真实值 \(y_i\), 如何衡量机器学习模型的效果? - 从测试集计算指标.

2.1 回归任务

均方误差

\[E(f ; D)=\frac{1}{m} \sum_{i=1}^{m}\left(f\left(\boldsymbol{x}_{i}\right)-y_{i}\right)^{2} \]

2.2 分类任务

错误率

\[E(f ; D)=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right) \]

精确率/精度

\[\begin{aligned} \operatorname{acc}(f ; D) &=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right)=y_{i}\right) =1-E(f ; D) \end{aligned} \]

下面是一些与混淆矩阵(confusion matrix)有关的概念.

查准率/准确率, precision, (找到的都对)

\[P=\frac{TP}{TP+FP} \]

查全率/召回率, recall, (可能对的都找到)

\[R = \frac{TP}{TP+FN} \]

\(F_1\) 和 \(F_\beta\), (权衡 precision 和 recall)

\[F_1 = \frac{2\times P\times R}{P+R} \]

\[F_\beta=\frac{(1+\beta^2)\times P \times R}{(\beta^2 \times P) + R} \]

• \(\beta = 1\), 标准 \(F_1\).

• \(\beta >1\), 偏重查全率 \(R\) (逃犯信息检索)

• \(\beta<1\), 偏重查准率 \(P\) (商品推荐系统)

\(ROC\) 曲线 \(AUC\)

• 分类器通常不是直接预测得到标签, 而是预测一个概率预测值, 然后将预测值(pred_prob)与分类阈值(threshold)进行比较.
  • \(\text{pred_prob} \ge \text{threshold}\), 认为是正类; 反之, 为反类.
• 根据每个样本的 \(\text{pred_prob}\), 可以对测试样本的预测结果进行排序; 最可能是正类的排在前, 最不可能是正类的排在后.
• 分类过程, 相当于在上一步的排序结果中, 选取一个截断点 (cut point), 之前的认为是正类, 之后的认为是负类.

\(\text{ROC}\), Reciver Operating Characteristic

• 根据预测结果 \(\text{pred_prob}\) 对测试样本排序.
• 逐个把样本作为正类进行预测 (相当于把 threshold 依次设置为每个样本的预测值 pred_prob), 每次设定后计算真正例率 \(\text{TPR}\) 和假正例率 \(\text{FPR}\).
• ROC 曲线: \(y\) 轴是 \(\text{TPR}\), \(x\) 轴是 \(\text{FPR}\).

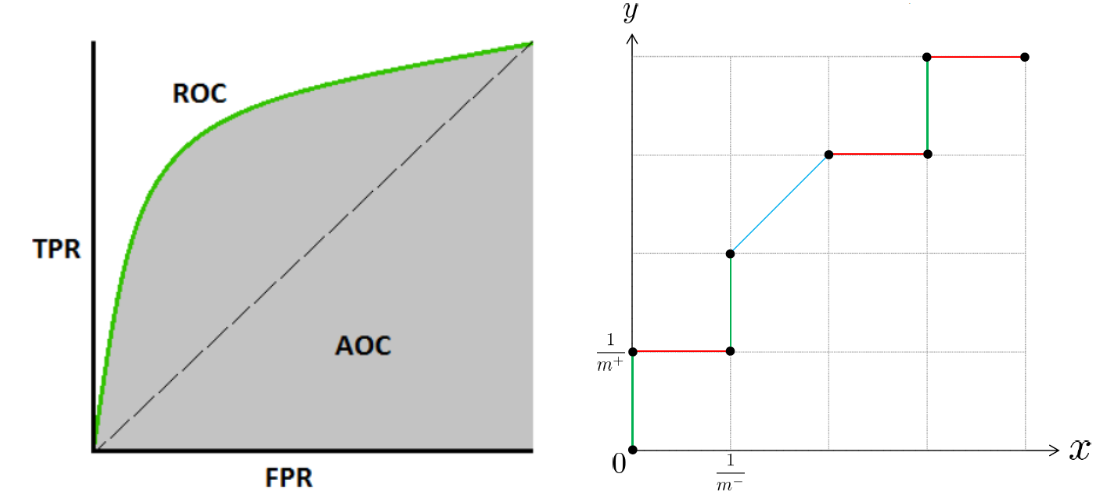
• 真正例率: \(\text{TPR} = \frac{TP}{TP+FN}\); 假正例率: \(\text{FPR} = \frac{FP}{TN+FP}\).

\(\text{AUC}\), Area Under ROC Curve

• \(\text{ROC}\) 曲线下方面积是 \(\text{AUC}\), Area Under ROC Curve.
• 有限样例的情况下, 可以用 \(\text{AUC}=\frac{1}{2}\sum_{i=1}^{m-1} (x_{i+1}-x_i)\cdot(y_i+y_{i+1})\). (梯形面积公式)
• \(\text{AUC}\) 考虑的是样本的排序质量 \(\text{AUC}=1-\ell_{\text {rank }}\)
  • 排序损失 \(\ell_{\text {rank }}=\frac{1}{m^{+} m^{-}} \sum_{x^{+} \in D^{+}} \sum_{x^{-} \in D^{-}}\left(\mathbb{I}\left(f\left(\boldsymbol{x}^{+}\right)<f\left(\boldsymbol{x}^{-}\right)\right)+\frac{1}{2} \mathbb{I}\left(f\left(\boldsymbol{x}^{+}\right)=f\left(\boldsymbol{x}^{-}\right)\right)\right)\)

三. 比较检验

测试集上的指标显示出的性能, 并不等于泛化性能. - 从测试性能推出泛化性能的把握有多大.

• 假设检验: 为比较分类器性能提供依据. 根据假设检验的结果, 我们可以推断出, 若在测试集上 \(A\) 比 \(B\) 好, 则 \(A\) 的泛化性能是否在统计意义上优于 \(B\) 的, 以及得到这个结论的把握有多大.
• 借助数理统计工具.

3.1 T-检验

• 多次重复留出法或者交叉验证法得到多组结果时, 可以使用"T-检验".

3.2 交叉验证T-检验

• 对不同学习器进行比较. \(k\) 折交叉验证, 成对T-检验.

3.2 偏差-方差分解

• 适用于回归任务, 拆解泛化误差.
  • 从三个方面进行定量: 算法, 数据, 任务.

泛化性能是由: 算法学习能力, 数据充分性以及学习任务本身的难度共同决定的.

References

• 高级机器学习 Lecture02
• 过拟合与欠拟合 https://zhuanlan.zhihu.com/p/72038532
• 西瓜书公式解析 https://github.com/datawhalechina/pumpkin-book/releases