[luogu p5410] 【模板】扩展 KMP（Z 函数） & 扩展 KMP（Z 函数）学习笔记

背景介绍

本文约定：字符串 \(S\) 的下标从 \(1\) 开始，\(n = |S|\)，\([p]\) 表示字符串的第 \(p\) 个字符，\([l, r]\) 表示 \([l], [l+1], \ldots, [r]\) 构成的 \(S\) 的子串。

\(z\) 函数的定义是：对于 \(1 \le x \le n\)，\(z(x)\) 定义为 \([1, n]\) 与 \([x, n]\) 的最长公共前缀（LCP）。

求解 \(z\) 函数的算法，可以在 \(\operatorname{O}(n)\) 的时间对所有 \(2 \le x \le n\) 求出 \(z(x)\)。

考虑到 \(z(1)\) 的特殊性，依据定义平凡地有 \(z(1) = n\)，但本算法中一般会令 \(z(1) = 0\)。

z 函数算法讲解

求 \(z\) 函数的算法流程是从前往后递推地，即在求解 \(z(x)\) 的时候，\(z(1), z(2), \ldots, z(x - 1)\) 的值均已被正确求出。

现在我们设算法正在求解 \(z(x)\)，则 \(z(1), z(2), \ldots, z(x - 1)\) 的函数值均已可被我们使用辅助计算 \(z(x)\)。不妨取 \(1 \le k < x\)，则：

注：事实上不一定有 \(x < k + z(k) - 1\)，但 \(x \ge k + z(k) - 1\) 的情形我们会在最后说明。

根据 \(z\) 函数的定义，我们已经有：

\[\begin{aligned}[] [1, z(k)] &= [k, k + z(k) - 1] \\ [1, x - k + 1] &= [k, x] \\ [x - k + 1, z(k)] &= [x, k + z(k) - 1] \end{aligned} \]

但 \(z(x)\) 想要的是 \([1, n]\) 与 \([x, n]\) 前缀上的联系，上面的等式却没有一条满足，一方字符串从 \(1\) 开始，另一方从 \(x\) 开始。

因此，我们再考虑引入一条信息：\(z(x - k + 1)\)，并记 \(l = z(x - k + 1)\)。

这里又会分出两种情况，先看如图所示的第一种：

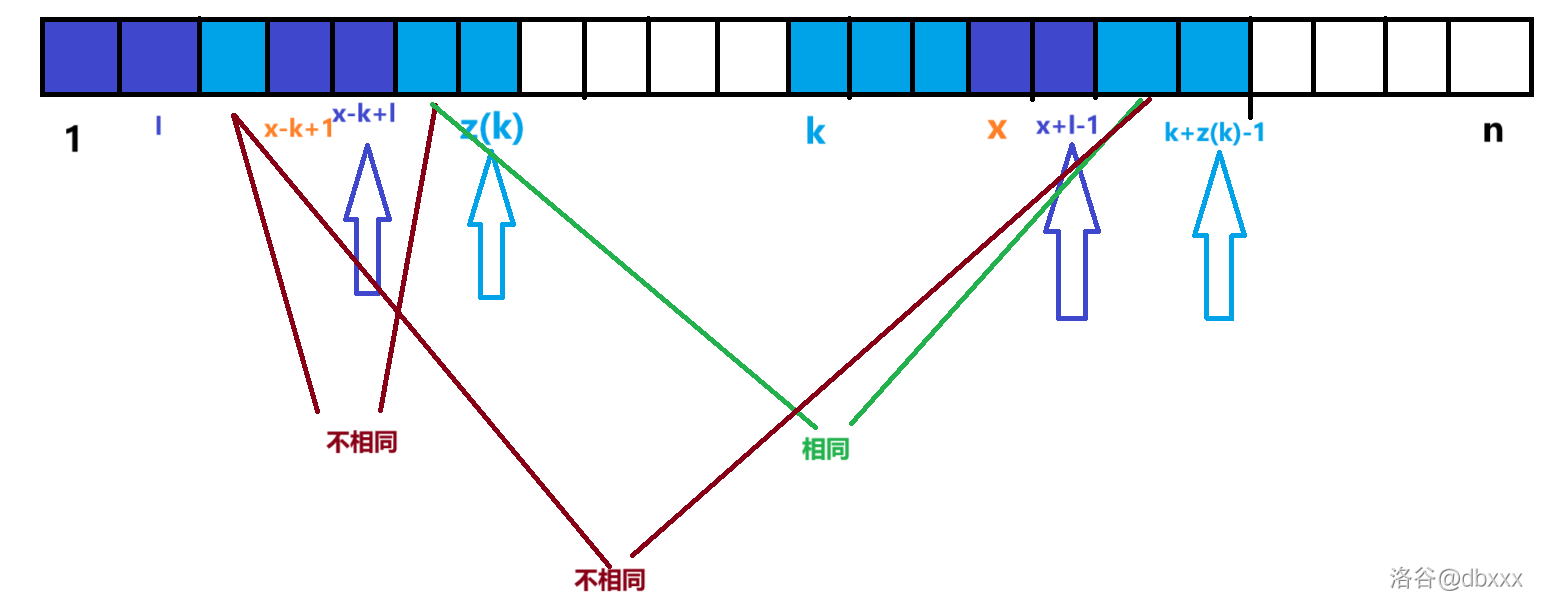
这张图对应的情况是 \(x - k + l < z(k)\)（紫色箭头需要严格小于蓝色箭头），此时 \(z(x)\) 的值已可确定：\(z(x) = l = z(x - k + 1)\)。

原因在于：

\[[x - k +1, z(k)] = [x, k + z(k) - 1] \implies [x - k + 1, x - k + l] = [x, x + l - 1] \land [x - k + l + 1] = [x + l] \]

即，第二个紫色块和第三个紫色块相等，且第二个紫色块后随字符与第三个紫色块后随字符相同。

（这里后随字符相同用到了上面的 \(x - k + l < z(k)\)，即取等都不可，否则会破坏这里的后随字符相同。）

请注意第二个紫色块和第三个紫色块相同的原因——它们在蓝色块代表的相同子串里，相同的相对位置。

\[z(x - k +1) = l \implies [x - k + 1, x - k + l] = [1, l] \land [l + 1] \ne [x - k + l + 1] \]

即，第二个紫色块和第一个紫色块相等，且第二个紫色块后随字符与第一个紫色块后随字符不同。

综合两者，我们就可以得到

\[[1, l] = [x, x + l - 1] \land [l + 1] \ne [x + l] \implies z(x) = l \]

即，第一个紫色块和第三个紫色块相等，且第一个紫色块后随字符与第三个紫色块后随字符不同。

前者保证了两个紫色块对应了 \([1, n]\) 和 \([x, n]\) 的一对公共前缀，而后者保证了这样的公共前缀是最长的。

第一种情况解决，我们再来看第二种情况：\(x - k + l \ge z(k)\)（紫色箭头大于等于蓝色箭头）：

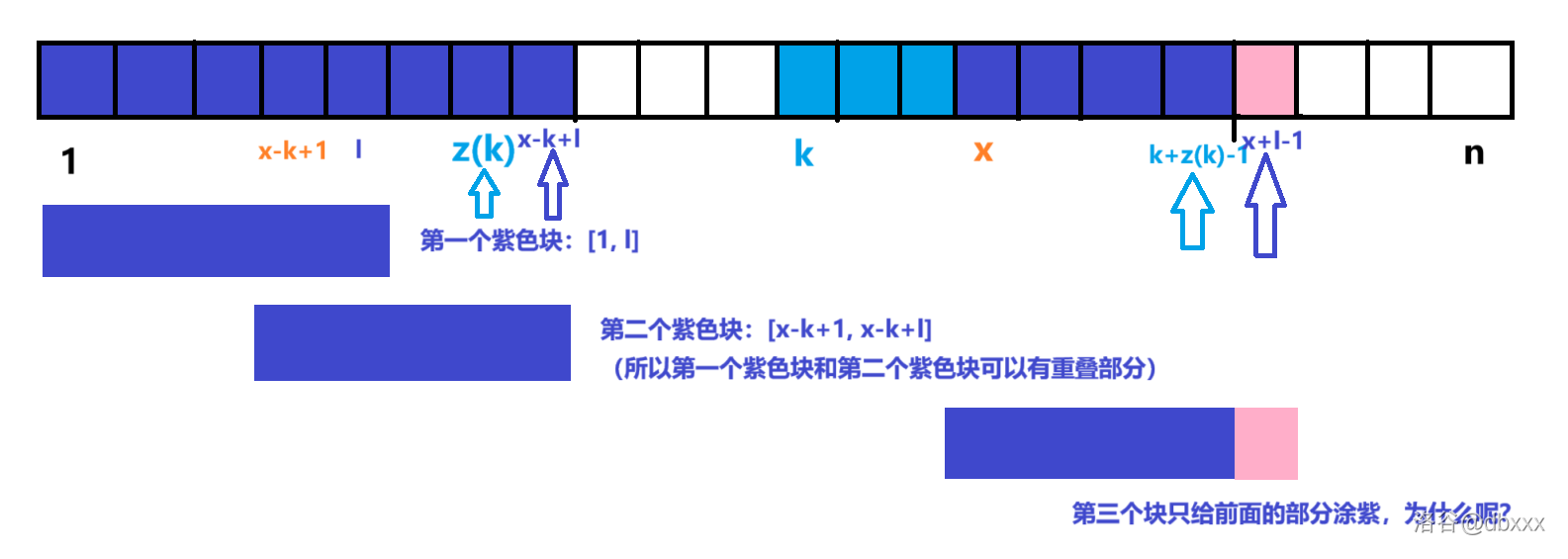
与第一种情况有何不同呢？答案是， 由于紫色箭头已经超过了蓝色箭头，意味着第二个紫色块和第三个紫色块已经不全部落于蓝色块内，此时超出蓝色块的部分不再保证相同，上图中把超出去的部分标记为了粉色。

还需注意的是，即使蓝紫色箭头重合，图中粉色的部分不存在，也不能简单得按照第一种情况，因为第一种情况要证明最长公共前缀，用到的后随字符不同的结论也会失效（即紫色可能不是最长的公共前缀）。

因此，我们现在只能确定不超出的部分仍然对应着 \([x, n]\) 和 \([1, n]\) 的一个公共前缀，但它不一定最长。即，我们此时只能确定 \(z(x) \ge k + z(k) - x\)（\([x, k + z(k) - 1]\) 的长度，在例图中是 \(4\)）。如何确定 \(z(x)\) 具体的值呢？

\(z\) 函数算法解决这个问题的思路相当简单：暴力跳。我们维护两个指针，初始分别在 \(k + z(k) - x + 1\) 和 \(k + z(k)\) 的位置，暴力同步向右跳跃判断是否相等。

\(l\) 现在对 \(z(x)\) 的求解已经没有什么帮助了，我们排除它的干扰重新绘图。

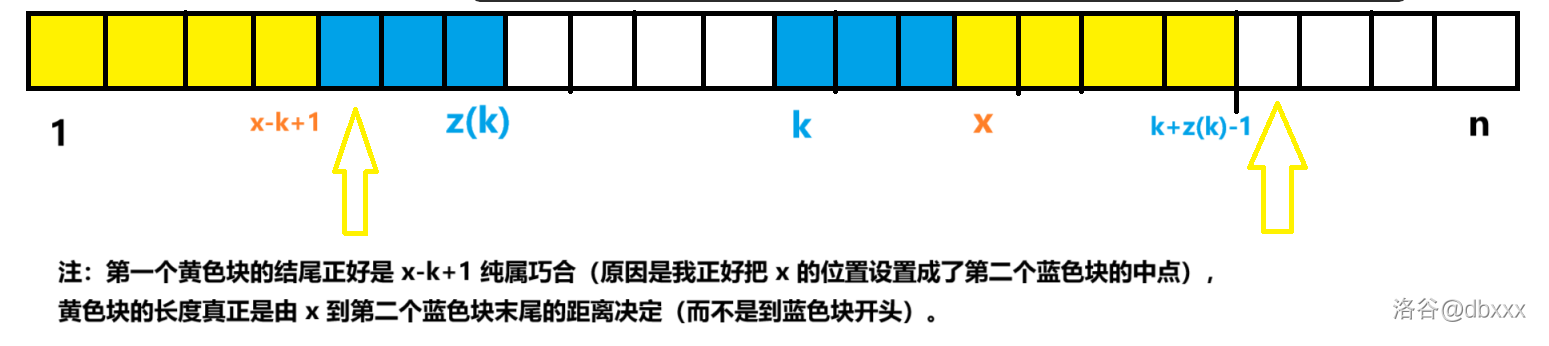
图中的两个黄色箭头就是指针。

然后就来到 \(z\) 函数算法的精髓了：如何让这个算法整体上的时间复杂度成为 \(\operatorname O(n)\)？谜底是最开始的时候，求解 \(z(x)\) 时 \(k\) 的选取规则：

• 在求解 \(z(2)\) 时，令 \(k \gets 1\)。
• 求解 \(z(x)\)，\(x \ge 2\) 之后：
  • 如果这一步的 \(z(x)\) 求解进入了第一种情况（紫色箭头严格小于蓝色箭头），那么 \(k\) 不变。
  • 如果这一步的 \(z(x)\) 求解进入了第二种情况（紫色箭头不小于蓝色箭头），此时令 \(k \gets x\)。

可以证明，在这个选取规则下，纵观全局（即求解所有 \(z(x)\) 的过程），暴力跳步骤中最右侧的黄色箭头一直单调向右走。只要证明了这一点，即可证暴力跳的均摊复杂度是 \(\operatorname O(n)\)，整个算法的复杂度的线性即可得证。

证明是这样的：求解 \(z(x)\) 时若进入了第二种情况，则暴力跳跃时右侧箭头实际上是从 \(k + z(k)\) 移动到了 \(x + z(x)\)。而此时令 \(k \gets x\)，那么下一次暴力跳跃时右侧箭头的起点 \(k + z(k)\) 其实就是这里的 \(x + z(x)\)。因此，右侧箭头整体上就是相当于从左到右扫了一遍，总体确实线性。

至此，\(z\) 函数的整个流程只剩下一个小问题仍待解决，即开头留下的：\(x \ge k + z(k) - 1\) 怎么办？这个时候肯定走第二种情况，问题在于此时算出来的指针位置 \(k + z(k) - x + 1\) 和 \(k + z(k)\) 可能退化为负数，此时修正一下指针的位置分别到 \(1\) 和 \(x\) 即可。

代码实现

void get_z(char *P) {
    int m = strlen(P) - 1;
    for (int i = 2, k = 1; i <= m; ++i) {
        if (k + z[k] - i <= z[i - k + 1]) { // 情况二
            // k + z[k] - i 是 i 到蓝色块末尾的长度，它如果小于等于紫色块的长度，则进入情况二
            z[i] = k + z[k] - i; // 先将 z[i] 设置为 i 到蓝色块末尾的长度
            if (z[i] < 0) // 长度可能求出 < 0 对应的是开头留下的小问题，x 本身超过蓝色块末尾，修正为 0 即可
                z[i] = 0;
            while (i + z[i] <= m && P[z[i] + 1] == P[i + z[i]]) // 暴力跳
                ++z[i];
            k = i; // k 的选取规则
        } else // 情况一
            z[i] = z[i - k + 1];
    }
    z[1] = m;
    return ;
}

exKMP 算法介绍

exKMP 求解的是模式串 \(P\) 与文本串 \(T\) 的每个后缀的最长公共前缀长度。

有了 z 函数基础，我们先直接来看 exKMP 的代码，这里 \(z_i\) 是 \(P\) 的 \(z\) 函数。

void exKMP(char *T, char *P) {
    int n = strlen(T) - 1, m = strlen(P) - 1;
    for (int i = 1, k = 1; i <= n; ++i) {
        if (k + p[k] - i <= z[i - k + 1]) {
            p[i] = k + p[k] - i;
            if (p[i] < 0)
                p[i] = 0;
            while (i + p[i] <= n && p[i] < m && P[p[i] + 1] == T[i + p[i]])
                ++p[i];
            k = i;
        } else
            p[i] = z[i - k + 1];
    }
    return ;
}

不难看出是大同小异的。为什么呢？因为 exKMP 实际上可以视作 \(z\) 函数算法流程的基础上，两个蓝色块分裂到两个不同的字符串中去。

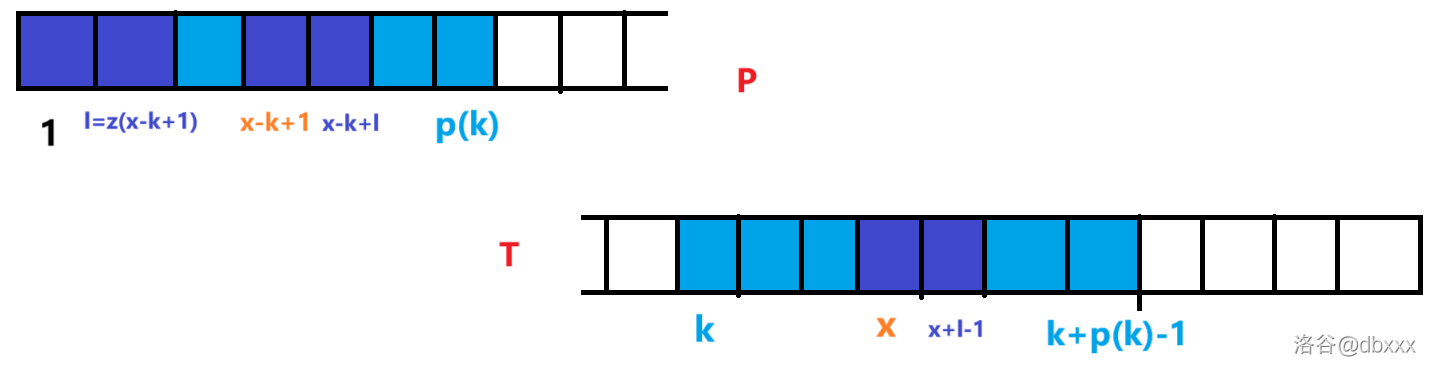
从上图就不难看出这个流程与 \(z\) 函数算法流程的高度相似性。\(z\) 函数算法流程我们用到的两个关键桥梁：

• 蓝色——对应 \(z(k)\) 的使用；
• 紫色——对应 \(z(x - k + 1)\) 的使用。

在这里因为分裂为两个字符串，蓝色部分变成了 \(p(k)\)，但紫色部分仍然对应的是 \(z(x - k + 1)\)。而其它与 \(z\) 函数的算法流程并无差异。