[luogu p2296] 寻找道路
寻找道路
题目描述
在有向图 \(G\) 中，每条边的长度均为 \(1\)，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：
- 路径上的所有点的出边所指向的点都直接或间接与终点连通。
- 在满足条件$ 1 $的情况下使路径最短。
注意：图 \(G\) 中可能存在重边和自环，题目保证终点没有出边。
请你输出符合条件的路径的长度。
输入输出格式
输入格式
第一行有两个用一个空格隔开的整数 \(n\) 和 \(m\)，表示图有 \(n\) 个点和 \(m\) 条边。
接下来的 \(m\) 行每行 \(2\) 个整数 \(x,y\)，之间用一个空格隔开，表示有一条边从点 \(x\) 指向点\(y\)。
最后一行有两个用一个空格隔开的整数 \(s, t\)，表示起点为 \(s\)，终点为 \(t\)。
输出格式
输出只有一行，包含一个整数，表示满足题目描述的最短路径的长度。如果这样的路径不存在，输出\(-1\)。
输入输出样例
输入样例 #1
3 2
1 2
2 1
1 3
输出样例 #1
-1
输入样例 #2
6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5
输出样例 #2
3
说明
解释1：
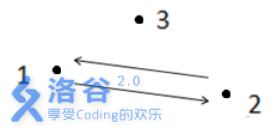
如上图所示，箭头表示有向道路，圆点表示城市。起点$1 $与终点\(3\)不连通，所以满足题目描述的路径不存在，故输出\(-1\) 。
解释2：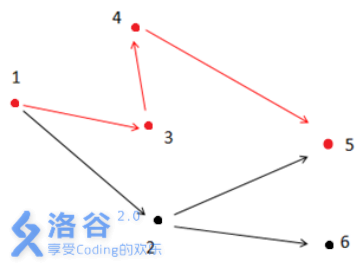 
如上图所示，满足条件的路径为\(1\)- >\(3\)- >\(4\)- >\(5\)。注意点\(2\) 不能在答案路径中，因为点\(2\)连了一条边到点\(6\) ，而点\(6\) 不与终点\(5\) 连通。
【数据范围】
对于\(30\%\)的数据，\(0 < n \le 10\)，\(0 < m \le 20\);
对于\(60\%\)的数据，\(0 < n \le 100\)，\(0 < m \le 2000\);
对于\(100\%\)的数据，\(0 < n \le 10000, 0 < m \le 200000,0 < x,y,s,t \le n, x,s \ne t\)。
分析
此题是一道很好的思路题。看似是一道图论，但这题不重在图论，而在搜索。（所以我没打图论的tag）
首先，一个点和终点的关系，在此题中可以有三种层层递进的特征：
- 无关系。（任意一个点）
- 与终点联通的点。
- 指向的节点都与终点联通的点。
显然题目要我们求的是，由3这种点组成的，连接起点和终点的最短路径。
什么是层层递进呢？也就是说，1这种点包含2这种点，2这种点包含3这种点。
那么此题就可以分作两步：
- 找满足3条件的点
- 求最短路径
求最短路径很简单，况且此题中所有边权都是1，你甚至不用什么最短路算法，直接bfs就可以解决。（如果需要最短路，我就会打上图论的tag了）
目前的问题是，怎么找满足3条件的点。其实刚刚已经剖析了，既然1包含2，2包含3，我们就可以在1中直接找2，然后再在2中找3就可以了。
找到2后，3就很好找了，直接判断这个点的所有边指向的节点是否满足2即可。
问题又变成了，怎么找2？
其实很简单，我们只需要反向建边，反向bfs就可以了。能反bfs到的点就是2点。
所以说，这题思路很妙，但是并不难想吧。
直接上代码：
代码
/*
* @Author: crab-in-the-northeast
* @Date: 2020-09-05 09:20:58
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2020-09-06 15:05:15
*/
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#include <algorithm>
const int maxn = 10005;
bool valid[maxn], link_end[maxn];
//valid是3点，link_end是2点。如果valid[i]是true代表i点为3点，link_end数组同理
int dis[maxn];//此点到起点的距离
std :: vector <int> side[maxn];//边
std :: vector <int> rev_side[maxn];//反向边
int main() {
int n, m;
std :: scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int u, v;
std :: scanf("%d%d", &u, &v);
side[u].push_back(v);
rev_side[v].push_back(u);
}
int s, t;
std :: scanf("%d%d", &s, &t);
link_end[t] = true;
std :: queue <int> q;
q.push(t);
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = rev_side[now].size() - 1; i >= 0; --i) {
int v = rev_side[now][i];
if (!link_end[v]) {
q.push(v);
link_end[v] = true;
}
}
}
if (!link_end[s]) {//注意，如果起始点就不和结尾点联通，那就不可能会有合法路径，直接输出-1即可
std :: printf("-1\n");
return 0;
}
for (int i = 1; i <= n; ++i)
if (link_end[i]) {
valid[i] = true;
for (int j = side[i].size() - 1; j >= 0; --j) {
int v = side[i][j];
if (!link_end[v]) {
valid[i] = false;
break;
}
}
}
if (!valid[s]) {//同理，如果起始点就不满足3点的条件，也应该直接输出-1
std :: printf("-1\n");
return 0;
}
dis[s] = 1;
while (!q.empty())
q.pop();
q.push(s);
while (!q.empty()) {
int now = q.front();
q.pop();
if (now == t) {
std :: printf("%d\n", dis[t] - 1);
return 0;
}
for (int i = side[now].size() - 1; i >= 0; --i) {
int v = side[now][i];
if (valid[v] && !dis[v]) {
dis[v] = dis[now] + 1;
q.push(v);
}
}
}
std :: printf("-1\n");//如果无路，-1
return 0;
}
