[luogu p1955] [NOI2015]程序自动分析
[NOI2015]程序自动分析
题目描述
在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本：假设 \(x_1,x_2,x_3,\cdots\) 代表程序中出现的变量，给定 \(n\) 个形如 \(x_i=x_j\) 或 \(x_i\neq x_j\) 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：\(x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1\)，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。
现在给出一些约束满足问题，请分别对它们进行判定。
输入输出格式
输入格式
输入的第一行包含一个正整数 \(t\)，表示需要判定的问题个数。注意这些问题之间是相互独立的。
对于每个问题，包含若干行：
第一行包含一个正整数 \(n\)，表示该问题中需要被满足的约束条件个数。接下来 \(n\) 行，每行包括三个整数 \(i,j,e\)，描述一个相等/不等的约束条件，相邻整数之间用单个空格隔开。若 \(e=1\)，则该约束条件为 \(x_i=x_j\)。若\(e=0\)，则该约束条件为 \(x_i\neq x_j\)。
输出格式
输出包括 \(t\) 行。
输出文件的第 \(k\) 行输出一个字符串 YES 或者 NO（字母全部大写），YES 表示输入中的第 \(k\) 个问题判定为可以被满足，NO 表示不可被满足。
输入输出样例
输入样例 #1
2
2
1 2 1
1 2 0
2
1 2 1
2 1 1
输出样例 #1
NO
YES
输入样例 #2
2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0
输出样例 #2
YES
NO
说明
【样例解释1】
在第一个问题中，约束条件为：\(x_1=x_2,x_1\neq x_2\)。这两个约束条件互相矛盾，因此不可被同时满足。
在第二个问题中，约束条件为：\(x_1=x_2,x_1 = x_2\)。这两个约束条件是等价的，可以被同时满足。
【样例说明2】 在第一个问题中，约束条件有三个：\(x_1=x_2,x_2= x_3,x_3=x_1\)。只需赋值使得 \(x_1=x_2=x_3\)，即可同时满足所有的约束条件。
在第二个问题中，约束条件有四个：\(x_1=x_2,x_2= x_3,x_3=x_4,x_4\neq x_1\)。由前三个约束条件可以推出 \(x_1=x_2=x_3=x_4\)，然而最后一个约束条件却要求 \(x_1\neq x_4\)，因此不可被满足。
【数据范围】
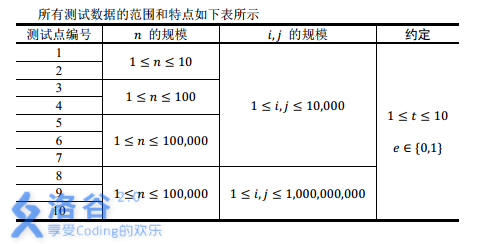
注：实际上 \(n\le 10^6\) 。
分析
此题没看数据范围前，很容易就能想出是一道并查集。先将所有等号连接的两个节点合并，再检查所有的不等限制，如果不等号两边的节点在同一个集合，说明他们相等，和不等矛盾，输出NO。如果所有都不矛盾，则输出YES。
但是实际细节中我们还要注意数据范围。\(1 \le i, j \le 1,000,000,000\)。这么大的范围开fa数组程序直接MLE到炸。但是又能注意到 \(1 \le n \le 100,000\)，也就是说 \(n\) 的范围不大，但是数字的范围大。而在此题中我们只关心节点数字的大小关系，并不关心具体数值，自然想到用离散化将所有数字节点离散到 \(n\) 以内，再进行并查集算法即可。
代码如下：
代码
/*
* @Author: crab-in-the-northeast
* @Date: 2020-08-19 18:52:22
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2020-08-20 01:57:10
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
const int maxn = 1000005;
int disc[maxn * 2], fa[maxn];
struct restrain {
int i, j, e;
}a[maxn];
int find(int x) {
while (x != fa[x]) x = fa[x] = fa[fa[x]];
return x;
}
void unite(int x, int y) {
fa[find(x)] = find(y);
return ;
}
bool check(int x, int y) {
return find(x) == find(y);
}
int main() {
int t;
std :: scanf("%d", &t);
while (t--) {
memset(a, 0, sizeof(a));
memset(disc, 0, sizeof(disc));
int n, discidx = 0;
bool flag = true;
std :: scanf("%d", &n);
//离散化。disc是discretization（离散化）的缩写。
//disc数组中，离散化数据从1开始保存，disc[0]代表disc数组一共有多少个离散化数据。
for (int i = 1; i <= n; ++i) {
std :: scanf("%d%d%d", &a[i].i, &a[i].j, &a[i].e);
disc[++discidx] = a[i].i;
disc[++discidx] = a[i].j;
}
std :: sort(disc + 1, disc + 1 + discidx);
disc[0] = std :: unique(disc + 1, disc + 1 + discidx) - disc - 1;
for (int i = 1; i <= n; ++i) {
a[i].i = std :: lower_bound(disc + 1, disc + 1 + disc[0], a[i].i) - disc - 1 + 1;
a[i].j = std :: lower_bound(disc + 1, disc + 1 + disc[0], a[i].j) - disc - 1 + 1;
}
//并查集开始
for (int i = 1; i <= disc[0]; ++i)
fa[i] = i;
for (int i = 1; i <= n; ++i)
if (a[i].e)
unite(a[i].i, a[i].j);//先合并所有等号
for (int i = 1; i <= n; ++i) {
if (!a[i].e) {
if (check(a[i].i, a[i].j)) {//同一集合，说明相等，与不等矛盾
std :: printf("NO\n");
flag = false;
break;
}
}
}
if (flag) std :: printf("YES\n");//所有都不矛盾
}
}
