[luogu p1807] 最长路
最长路
题目描述
设 \(G\) 为有 \(n\) 个顶点的带权有向无环图，\(G\) 中各顶点的编号为 \(1\) 到 \(n\)，请设计算法，计算图 \(G\) 中 \(<1,n>\) 间的最长路径。
输入输出格式
输入格式
输入的第一行有两个整数，分别代表图的点数 \(n\) 和边数 \(m\)。
第 \(2\) 到第 \((m + 1)\) 行，每行 \(3\) 个整数 \(u, v, w\)，代表存在一条从 \(u\) 到 \(v\) 边权为 \(w\) 的边。
输出格式
输出一行一个整数，代表 \(1\) 到 \(n\) 的最长路。
若 \(1\) 与 \(n\) 不联通，请输出 \(-1\)。
输入输出样例
输入样例 #1
2 1
1 2 1
输出样例 #1
1
说明
数据规模与约定
- 对于 \(20\%\)的数据，\(n \leq 100\)，\(m \leq 10^3\)。
- 对于 \(40\%\) 的数据，\(n \leq 10^3\)，\(m \leq 10^{4}\)。
- 对于 \(100\%\) 的数据，\(1 \leq n \leq 1500\)，\(1 \leq m \leq 5 \times 10^4\)，\(1 \leq u, v \leq n\)，\(-10^5 \leq w \leq 10^5\)。
分析
此题有两种解法。一是最短路魔改，二是拓扑排序。
最短路魔改这个解法相信很简单，用支持负图的最短路算法（比如SPFA，BF等），将所有边权值取反，跑最短路，然后结果再取反即可。当然不支持负图的最短路算法，比如dij，也可以通过更改一些内容来实现最长路，这些都是很简单的，不再细说。
拓扑排序解法也很简单。定义 \(dis_i\) 为 \(1 \rightarrow i\) 的最短路径， \(ind_i\) 为 \(i\) 节点的入度，\(flag_i\) 为 \(i\) 节点是否与 \(1\) 节点连通。算法如下：
- 设置 \(ind\)，\(dis_n\) 设置为 \(-1\)，\(flag_1\) 设置为true。
- 将所有满足 \(ind_i = 0\) 的 \(i\) push进队列 \(q\)。
- 若队列非空，取队列第一个作为节点 \(u\)，并pop掉该节点。
- 遍历 \(u\) 指向的点 \(v\)，令 \(ind_v - 1 \rightarrow ind_v\)。
- 若 \(flag_u\) 为true，且 \(dis_v < dis_u + w\)（\(w\) 为 \(u \rightarrow v\) 这条边的权值），那么令 \(dis_v = dis_u + w\)。（最长路核心步骤）
- 另外，如果 \(flag_u\) 为true，那么 \(flag_v\) 也要设置为 true。
- 如果 \(ind_v = 0\)，将 \(v\) 节点入队 \(q\)。
- 重复 \(3 \sim 7\) 步，直到 \(q\) 队列为空。此时的 \(dis_n\) 即为 \(1 \rightarrow n\) 的最长路。
这个算法的正确性也挺显然的。如果 \(ind_u = 0\)，那么 \(dis_u\) 就会变为定值。
那就上代码吧。
代码
/*
* @Author: crab-in-the-northeast
* @Date: 2020-09-25 21:24:06
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2020-09-26 11:36:28
*/
#include <iostream>
#include <cstdio>
#include <queue>
#include <vector>
const int maxn = 1505;
const int maxm = 50005;
struct edge {
int u, v, dis;
};
int n, m;
std :: vector <edge> G[maxn];
int ind[maxn], dis[maxn];
bool flag[maxn];
void topsort() {
flag[1] = true;
std :: queue <int> q;
for (int i = 1; i <= n; ++i)
if (ind[i] == 0)
q.push(i);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i].v;
--ind[v];
if (flag[u]) {
if (dis[v] < dis[u] + G[u][i].dis)
dis[v] = dis[u] + G[u][i].dis;
flag[v] = true;
}
if (ind[v] == 0)
q.push(v);
}
}
}
int main() {
std :: scanf("%d %d", &n, &m);
for (int i = 1; i <= m; ++i) {
edge now;
std :: scanf("%d %d %d", &now.u, &now.v, &now.dis);
G[now.u].push_back(now);
++ind[now.v];
}
dis[n] = -1;
topsort();
std :: printf("%d\n", dis[n]);
return 0;
}
番外：一个错误的解法
有些人可能会说，啊东北小蟹蟹，你一开始就把所有的 \(ind_i = 0\) 的 \(i\) 都入队了，这是对的，但是感觉有点浪费，如果我把所有满足 \(ind_i = 0\) 且 \(i \neq 1\) 的节点的出边都砍掉，然后直接从1开始，不会很省时间吗？
但实际上，这个解法是错误的。来举一个反例：
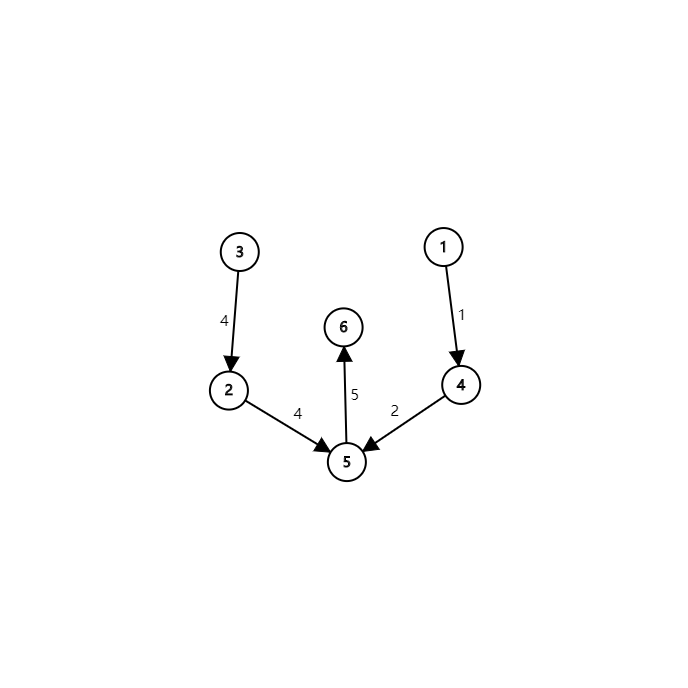
如果按照这个算法，一开始是先删除了 \(3 \rightarrow 2\) 这条边，然后进入拓扑，\(4 \rightarrow 5\)。到这里都是正常的，但是从 \(5\) 开始出现了问题。因为有 \(2 \rightarrow 5\) 这条边，所以 \(ind_5 \neq 0\)，因此 \(5\) 没有入队，于是算法提前迷之结束了，也就是说算法认为 \(1 \rightarrow 6\) 不连通。离谱吧？
但是，这个算法还真的可过这道题……为什么呢？
蟹蟹的推测是，数据是按照若 \(u \rightarrow v \in G\)，那么 \(u < v\) 来造的。如果数据一定满足这个条件，那么这个算法就是没问题的。这又是为什么呢？
再来举一个和刚刚非常相似的例子。
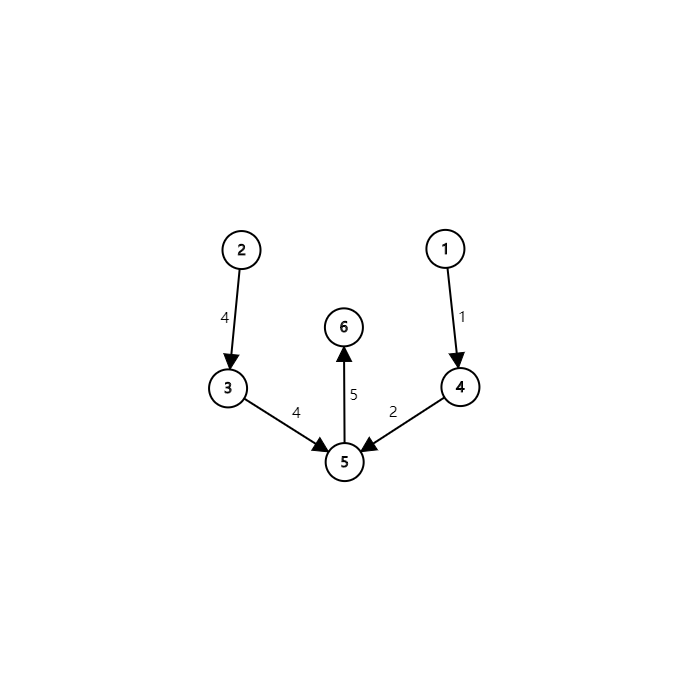
区别在哪里？没错，\(2\) 和 \(3\) 序号颠倒了。你可能想问了，这和刚刚有什么区别啊？算法不还是认为 \(1 \rightarrow 6\) 不连通吗？
你想，我从 \(2 \rightarrow n\) 删边，那么我首先删了 \(2 \rightarrow 3\) 这条边，那么 \(ind_3\) 变为了 \(0\)。如下图：
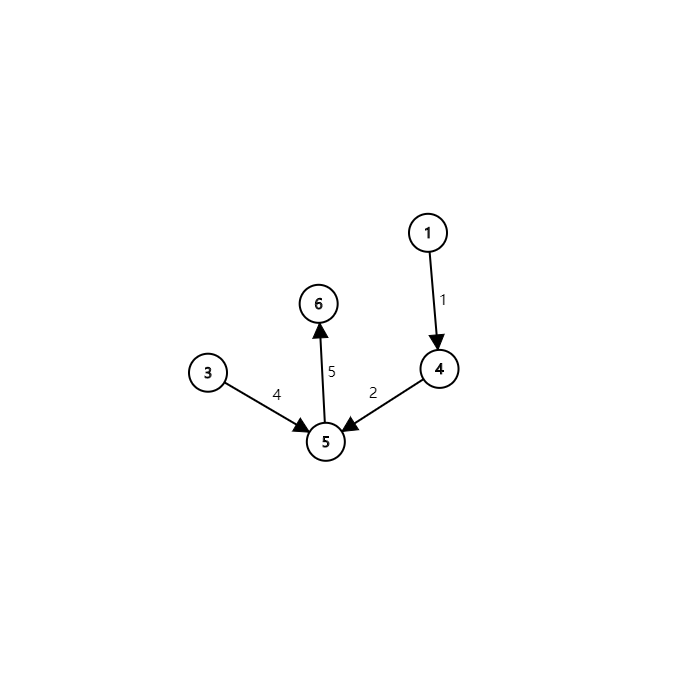
此时开始到 \(3\) 号节点。发现 \(ind_3 = 0\)，因此算法会把 \(3 \rightarrow 5\) 这条边删掉。如下：
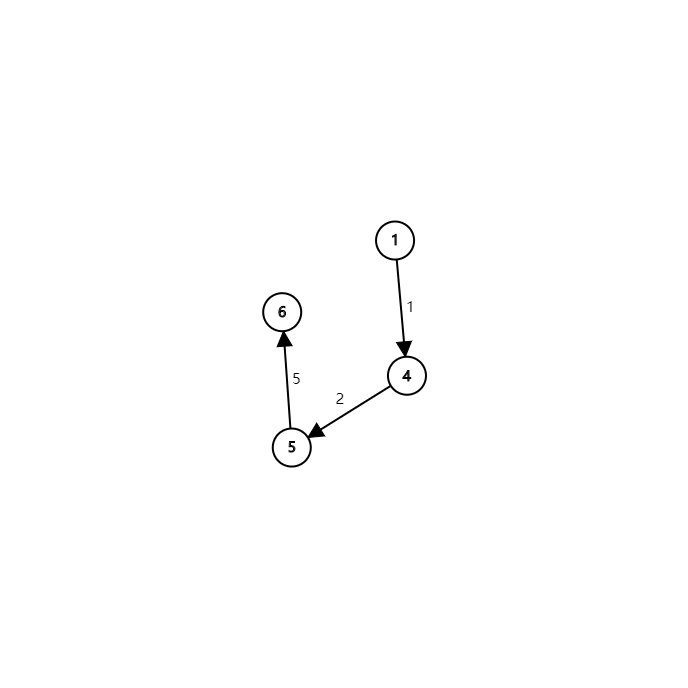
此时再运行拓扑排序，答案就是正常的，为 \(8\)。而最开始的那张图呢？
算法会先尝试处理 \(2\)，发现 \(ind_2 \neq 0\)，因此没有任何变化，转而处理 \(3\)，删掉了 \(3 \rightarrow 2\) 这条边。但是 \(2 \rightarrow 5\) 这条边并没有成功删除，因此 \(5\) 节点变成了死点。
