[luogu p1228] 地毯填补问题
地毯填补问题
题目描述
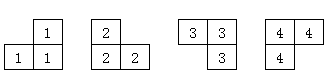
相传在一个古老的阿拉伯国家里，有一座宫殿。宫殿里有个四四方方的格子迷宫，国王选择驸马的方法非常特殊，也非常简单：公主就站在其中一个方格子上，只要谁能用地毯将除公主站立的地方外的所有地方盖上，美丽漂亮聪慧的公主就是他的人了。公主这一个方格不能用地毯盖住，毯子的形状有所规定，只能有四种选择（如图）：
并且每一方格只能用一层地毯，迷宫的大小为 \(2^k\times 2^k\) 的方形。当然，也不能让公主无限制的在那儿等，对吧？由于你使用的是计算机，所以实现时间为 \(1\mathrm s\)。
输入输出格式
输入格式
输入文件共 \(2\) 行。
第一行：\(k\)，即给定被填补迷宫的大小为 \(2^k\times 2^k\)（\(0\lt k\leq 10\)）；
第二行：\(x,y\)，即给出公主所在方格的坐标（\(x\) 为行坐标，\(y\) 为列坐标），\(x\) 和 \(y\) 之间有一个空格隔开。
输出格式
将迷宫填补完整的方案：每一补(行)为\(x\ y\ c\)（\(x,y\) 为毯子拐角的行坐标和列坐标， \(c\) 为使用毯子的形状，具体见上面的图 \(1\)，毯子形状分别用 \(1,2,3,4\) 表示，\(x,y,c\) 之间用一个空格隔开）。
输入输出样例
输入样例 #1
3
3 3
输出样例 #1
5 5 1
2 2 4
1 1 4
1 4 3
4 1 2
4 4 1
2 7 3
1 5 4
1 8 3
3 6 3
4 8 1
7 2 2
5 1 4
6 3 2
8 1 2
8 4 1
7 7 1
6 6 1
5 8 3
8 5 2
8 8 1
说明
事实上感觉四个的形状分别是这样（仅供参考，如果有问题联系 icy）
spj 报错：
- \(c\) 越界
- \(x,y\) 越界
- \(mp[x][y]\) 已被占用
- \(mp[x][y]\) 从未被使用
分析
乍一看这个样例，好像找不出什么规律。那么我们就从\(k = 1\)的情况开始讨论吧。
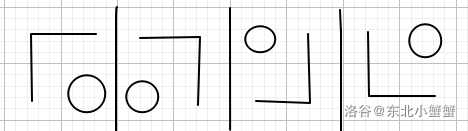
首先\(k = 1\)，代表填补迷宫的大小为\(2 \times 2\)，这也就是最基础的情况（接下来的所有图，圆圈代表公主，横条状的东西代表地毯）。可能出现的情况有四种：
那么\(k = 2\)呢？这就代表了填补迷宫的大小为\(4 \times 4\)。这样情况一多，怎么办呢？
其实只需要填补一个地毯：
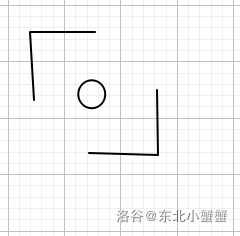
然后你就会发现，\(4 \times 4\)分解为了\(4\)个\(2 \times 2\)的区块，而填补的这个地毯把右上，左下和右下的\(2 \times 2\)区块全部覆盖了一格。显然这又回到了\(2 \times 2\)的情况，根据上边的四种选择填补即可。
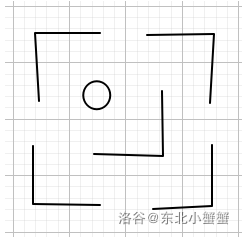
接下来扩展到\(k = 3\)的情况，也就是变成了\(8 \times 8\)。我们还是像刚刚一样，在中间填补一个地毯：
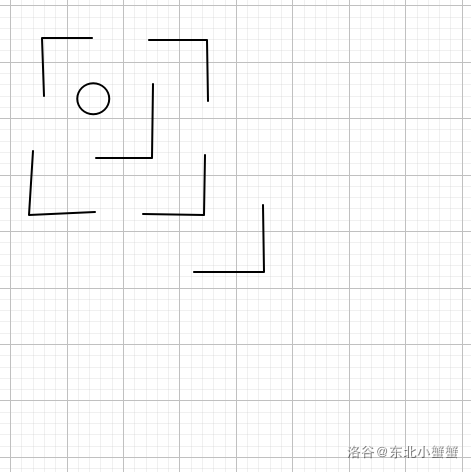
这样填补的这个地毯把右上，左下和右下的\(4 \times 4\)区块全部覆盖了一格。显然这又回到了\(4 \times 4\)的情况。而\(4 \times 4\)的情况再分解成\(4\)个\(2 \times 2\)的区块。
熟悉的套路，熟悉的料理。
以此类推，\(2 ^ k \times 2 ^ k\)的情况总能分解成\(4\)个\(2 ^ {k - 1} \times 2 ^ {k - 1}\)的情况，直到\(k = 2\)的基本情况。
妥妥的递归，代码走起吧！
代码
/*
* @Author: crab-in-the-northeast
* @Date: 2020-04-29 10:48:00
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2020-05-02 01:10:17
*/
#include <iostream>
#include <cstdio>
void solve(int x1, int y1, int x2, int y2, int n) {
if(n == 1) return ;
if(x1 - x2 < (n >> 1)) {
if(y1 - y2 < (n >> 1)) {
std :: cout << (x2 + (n >> 1)) << ' ' << (y2 + (n >> 1)) << ' ' << 1 << std :: endl;
solve(x1, y1, x2, y2, (n >> 1));
solve(x2 + (n >> 1) - 1, y2 + (n >> 1), x2, y2 + (n >> 1), (n >> 1));
solve(x2 + (n >> 1), y2 + (n >> 1) - 1, x2 + (n >> 1), y2, (n >> 1));
solve(x2 + (n >> 1), y2 + (n >> 1), x2 + (n >> 1), y2 + (n >> 1), (n >> 1));
} else {
std :: cout << (x2 + (n >> 1)) << ' ' << (y2 + (n >> 1) - 1) << ' ' << 2 << std :: endl;
solve(x2 + (n >> 1) - 1, y2 + (n >> 1) - 1, x2, y2, (n >> 1));
solve(x1, y1, x2, y2 + (n >> 1), (n >> 1));
solve(x2 + (n >> 1), y2 + (n >> 1) - 1, x2 + (n >> 1), y2, (n >> 1));
solve(x2 + (n >> 1), y2 + (n >> 1), x2 + (n >> 1), y2 + (n >> 1), (n >> 1));
}
} else {
if(y1 - y2 < (n >> 1)) {
std :: cout << (x2 + (n >> 1) - 1) << ' ' << (y2 + (n >> 1)) << ' ' << 3 << std :: endl;
solve(x2 + (n >> 1) - 1, y2 + (n >> 1) - 1, x2, y2, (n >> 1));
solve(x2 + (n >> 1) - 1, y2 + (n >> 1), x2, y2 + (n >> 1), (n >> 1));
solve(x1, y1, x2 + (n >> 1), y2, (n >> 1));
solve(x2 + (n >> 1), y2 + (n >> 1), x2 + (n >> 1), y2 + (n >> 1), (n >> 1));
} else {
std :: cout << (x2 + (n >> 1) - 1) << ' ' << (y2 + (n >> 1) - 1) << ' ' << 4 << std :: endl;
solve(x2 + (n >> 1) - 1, y2 + (n >> 1) - 1, x2, y2, (n >> 1));
solve(x2 + (n >> 1) - 1, y2 + (n >> 1), x2, y2 + (n >> 1), (n >> 1));
solve(x2 + (n >> 1), y2 + (n >> 1) - 1, x2 + (n >> 1), y2, (n >> 1));
solve(x1, y1, x2 + (n >> 1), y2 + (n >> 1), (n >> 1));
}
}
}
int main() {
int k, x, y;
std :: cin >> k >> x >> y;
solve(x, y, 1, 1, 1 << k);
return 0;
}
评测记录
前面那些WA14都是在递归函数中出了细节错误。
