Solution - 切蛋糕

切蛋糕 题解

题目描述

\(\rm Alice\)、\(\rm Bob\) 和 \(\rm Cindy\) 三个好朋友得到了一个圆形蛋糕，他们打算分享这个蛋糕。

三个人的需求量分别为 \(a,b,c\)，现在请你帮他们切蛋糕，规则如下：

\(1.\) 每次切蛋糕可以选择蛋糕的任意一条直径，并沿这条直径切一刀（注意切完后不会立刻将蛋糕分成两部分）。

\(2.\) 设你一共切了 \(n\) 刀，那么你将得到 \(2n\) 个扇形的蛋糕（特别地，切了 \(0\) 刀被认为是有一个扇形，即整个圆形蛋糕），将这些蛋糕分配给 \(\rm Alice\)，\(\rm Bob\) 和 \(\rm Cindy\)，要求每个扇形蛋糕只能完整地分给一个人。

\(3.\) 三人分到的蛋糕面积比需要为 \(a : b : c\)（不保证是最简比例，且如果 \(a : b : c\) 中某个数为 \(0\)，表示那个人不吃蛋糕）。

为了完成这个任务，你至少需要切几刀？

输入格式

从文件 \(cake.in\) 中读入数据

本题单个测试点包含多组数据。

第一行包含一个整数 \(T\)，表示数据组数。

接下来 \(T\) 行，每行包含三个整数 \(a,b, c\)，表示三人的需求量。

样例1输入

6
0 0 8
0 5 3
9 9 0
6 2 4
1 7 4
5 8 5

样例1输出

0
2
1
2
3
2

样例1解释

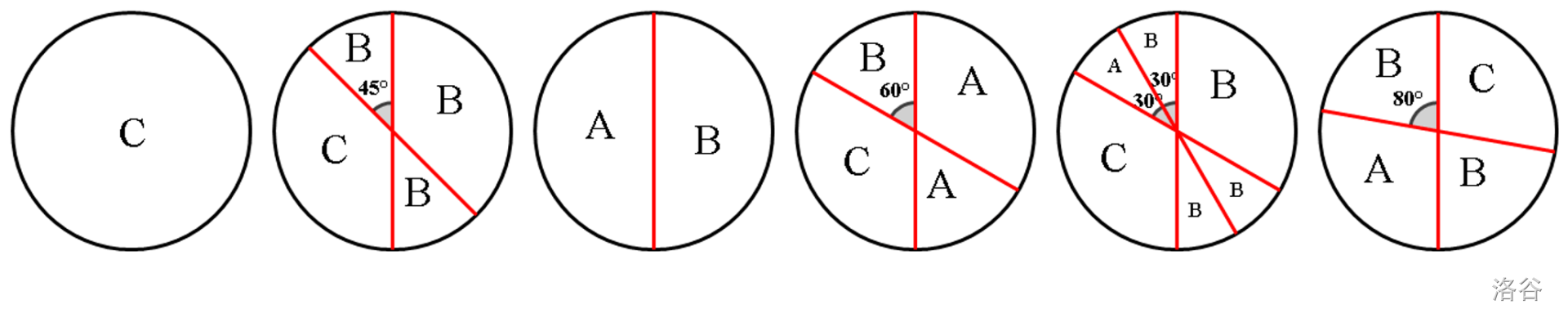
数据范围与提示

\(30\%\) 的数据满足\(:\) \(a = b = 0。\)

\(60\%\) 的数据满足\(:\) \(a = 0。\)

\(100\%\) 的数据满足\(:\) \(1 ≤ T ≤ 10^4, 0 ≤ a,b,c ≤ 10^8, 保证\ a + b + c > 0。\)

思路

看到数据范围，马上排除算角度暴力求解（精度不够）

我们假设 \(a ≤ b ≤ c\)

情况 \(1:\) 如果 \(a = 0\) 且 \(b = 0\) 时, 剩下的根本不用切，输出 \(0.\)

情况 \(2:\) 当 \(a = 0\) 时，若 \(b = c\) 输出 \(1,\) 否则输出 \(2。\)

情况 \(3:\) 当 \(a ≠ 0\) 时，若 \(a = b\) 或 \(b = c\) 或 \(a + b = c\) 输出 \(2\), 否则为 \(3。\)

code

#include <cstdio>
#include <algorithm>
using namespace std;
int a[5];
int main() {
	freopen("cake.in", "r", stdin);
	freopen("cake.out", "w", stdout);
	int t;
	scanf("%d", &t);
	while (t--) {
		scanf("%d %d %d", &a[1], &a[2], &a[3]);
		sort(a + 1, a + 3 + 1);
		if (a[1] == 0 && a[2] == 0) {
			printf("0\n");
		} else if (a[1] == 0) {
			if (a[2] == a[3]) {
				printf("1\n");
			} else {
				printf("2\n");
			}
		} else {
			if (a[1] == a[2] || a[2] == a[3] || a[1] + a[2] == a[3]) {
				printf("2\n");
			} else printf("3\n");
		}
	}
	return 0;
}