题目：https://www.luogu.org/problem/P4719

 

题解：

首先要对矩阵有一定的基础知识

1、多个等大的方阵的乘法是具有结合律的

2、当某两种运算满足分配律时，矩阵的乘法是可以重新定义为这两种运算，且新的乘法也满足结合律

3、矩阵加速不仅可以加速递推，还可以加速floyd、某些DP等可以通过重新定义矩阵乘法的算法

 

接下来进入正题：

如题，我们设f[u][0]/f[u][1]分别表示节点u选/不选的子树最大权独立集的权值

于是可以写出一个明显的DP式

f[u][0]=\sum_{son}(max(f[son][0],f[son][1]))

f[u][1]=\sum_{son}(f[son][0])+val[u]

由于加法和max是满足分配律的，即

max(a,b)+c=max(a+c,b+c)

于是我们可以重新定义矩阵的乘法：（乘法可以分配进入加法，加法可以分配进入max）

A*B=\sum_{i=1}^n\sum_{j=1}^nmax_{k=1}^n(A[i][k]+B[k][j])

那我们如何表达上面的DP式呢？

 

想一下，如果要修改一个点的权值，它会影响的DP值只有他到它祖先的一条链DP值

于是我们可以先来考虑一个简单的情况：树是一条链

那么上面的DP式就可以用矩阵写为：（其中矩阵乘法是重新定义了的！）

\begin{bmatrix} 0&0\\ val[u]&-inf \end{bmatrix} *\begin{bmatrix} f[son][0]\\ f[son][1] \end{bmatrix}= \begin{bmatrix} f[u][0]\\ f[u][1] \end{bmatrix}

我们把矩阵乘法展开，发现它刚好是

f[u][0]=max(0+f[son][0],0+f[son][1])

f[u][1]=max(val[u]+f[son][0],f[son][1]-inf)

由于inf非常大，所以f[son][1]在第二个DP式中的贡献可以不计

又因为这种乘法是满足结合律的

所以想到了什么？

对！线段树！！！这样就可以修改了

于是我们就解决了带修改的一条链的DP（真是一个伟大的进步！）

 

然后我们继续想，一棵树的情况怎么办？

似乎可以树链剖分？？但是又不知道具体怎么实现。。。

我们可以重新定义每个点的初始矩阵

由于一个点走到根节点最多会经过logn条轻边

于是我们可以把每个点的初始矩阵定为：

\begin{bmatrix} g[u][0] &g[u][0] \\ g[u][1] & -inf \end{bmatrix}

g[u][0/1]表示节点u选/不选的所有轻儿子的贡献之和

重链上的子孙就可以通过树链剖分+线段树来计算：

\begin{bmatrix} g[u][0] &g[u][0] \\ g[u][1] & -inf \end{bmatrix}* \begin{bmatrix} f[son][0]&f[son][0] \\ f[son][1]&f[son][1] \end{bmatrix}= \begin{bmatrix} f[u][0] &f[u][0] \\ f[u][1] &f[u][1] \end{bmatrix}

（请读者自行展开验证）

先来想一下如何计算一个点的答案：

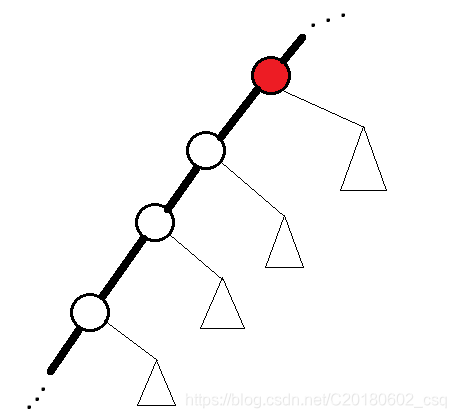
由图可知：我们若要计算一个点的贡献就需要把它所在的重链以下的点的答案都要统计一遍

考虑如何修改，如图：

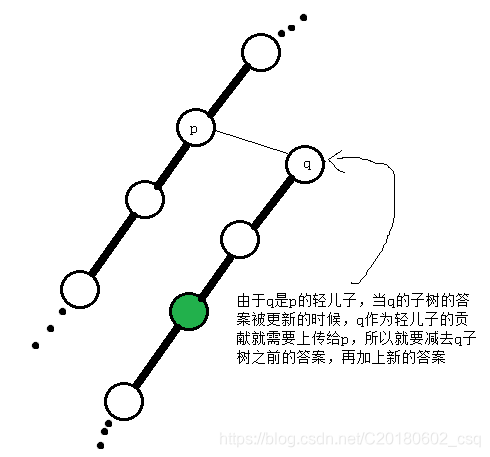
就讲完啦

 

代码可以先尝试着自己写（其实并不难写，但是比较难调，后来发现INF开大了，调了40min）

代码（人生第一道动态DP）：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
inline int gi()
{
	char c;int num=0,flg=1;
	while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
	while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
	return num*flg;
}
#define N 100005
const int INF=0x3f3f3f3f;
int fir[N],to[2*N],nxt[2*N],cnt;
void adde(int a,int b)
{
	to[++cnt]=b;nxt[cnt]=fir[a];fir[a]=cnt;
	to[++cnt]=a;nxt[cnt]=fir[b];fir[b]=cnt;
}
int val[N];
int dep[N],fa[N],siz[N],son[N],top[N],bot[N];
void dfs1(int u)
{
	dep[u]=dep[fa[u]]+1;
	int v,p;siz[u]=1;
	for(p=fir[u];p;p=nxt[p]){
		v=to[p];
		if(v!=fa[u]){
			fa[v]=u;dfs1(v);
			siz[u]+=siz[v];
			if(siz[son[u]]<siz[v])
				son[u]=v;
		}
	}
}
int pos[N],dc,ind[N];
int dfs2(int u)
{
	pos[u]=++dc;ind[dc]=u;
	if(son[u]) top[son[u]]=top[u],bot[u]=dfs2(son[u]);
	else return bot[u]=u;
	int v,p;
	for(p=fir[u];p;p=nxt[p]){
		v=to[p];
		if(v!=fa[u]&&v!=son[u])
			top[v]=v,bot[v]=dfs2(v);
	}
	return bot[u];
}
int f[N][2];
void DP(int u)
{
	f[u][1]=val[u];
	int v,p;
	for(p=fir[u];p;p=nxt[p]){
		v=to[p];
		if(v!=fa[u]){
			DP(v);
			f[u][0]+=max(f[v][0],f[v][1]);
			f[u][1]+=f[v][0];
		}
	}
}
#define lc i<<1
#define rc i<<1|1
struct node{
	int l,r,x[2][2];
	node(){}
	node(int a,int b,int c,int d,int _l,int _r){l=_l;r=_r;x[0][0]=a;x[0][1]=b;x[1][0]=c;x[1][1]=d;}
	node operator * (const node &t)const{
		return node(max(x[0][0]+t.x[0][0],x[0][1]+t.x[1][0]),
			    max(x[0][0]+t.x[0][1],x[0][1]+t.x[1][1]),
			    max(x[1][0]+t.x[0][0],x[1][1]+t.x[1][0]),
			    max(x[1][0]+t.x[0][1],x[1][1]+t.x[1][1]),l,t.r);
	}
}a[N<<2];
int g[N][2];
void build(int i,int l,int r)
{
	a[i].l=l;a[i].r=r;
	if(l==r){
		int u=ind[l],v,p;
		g[u][0]=0;g[u][1]=val[u];
		for(p=fir[u];p;p=nxt[p]){
			v=to[p];
			if(v!=fa[u]&&v!=son[u]){
				g[u][0]+=max(f[v][0],f[v][1]);
				g[u][1]+=f[v][0];
			}
		}
		a[i]=node(g[u][0],g[u][0],g[u][1],-INF,l,r);
		return;
	}
	int mid=(l+r)>>1;
	build(lc,l,mid);build(rc,mid+1,r);
	a[i]=a[lc]*a[rc];
}
void insert(int i,int x)
{
	if(x>a[i].r||a[i].l>x) return;
	if(a[i].l==x&&a[i].r==x){
		a[i]=node(g[ind[x]][0],g[ind[x]][0],g[ind[x]][1],-INF,a[i].l,a[i].r);
		return;
	}
	insert(lc,x);insert(rc,x);
	a[i]=a[lc]*a[rc];
}
node x,y,ans;
void query(int i,int l,int r)
{
	if(l>a[i].r||a[i].l>r) return;
	if(l<=a[i].l&&a[i].r<=r){
		if(ans.l==-1) ans=a[i];
		else ans=ans*a[i];
		return;
	}
	query(lc,l,r);query(rc,l,r);
}
void modify(int u,int w)
{
	g[u][1]+=(w-val[u]);val[u]=w;
	while(u){
		ans.l=-1;query(1,pos[top[u]],pos[bot[u]]);x=ans;
		insert(1,pos[u]);
		ans.l=-1;query(1,pos[top[u]],pos[bot[u]]);y=ans;
		u=fa[top[u]];if(!u) break;
		g[u][1]+=y.x[0][0]-x.x[0][0];
		g[u][0]+=max(y.x[0][0],y.x[1][0])-max(x.x[0][0],x.x[1][0]);
	}
}
int main()
{
	int n,Q,i,u,v;;
	n=gi();Q=gi();
	for(i=1;i<=n;i++)
		val[i]=gi();
	for(i=1;i<n;i++){
		u=gi();v=gi();
		adde(u,v);
	}
	dfs1(1);
	top[1]=1;dfs2(1);
	DP(1);
	build(1,1,n);
	for(i=1;i<=Q;i++){
		u=gi();v=gi();
		modify(u,v);
		ans.l=-1;query(1,pos[top[1]],pos[bot[1]]);
		printf("%d\n",max(ans.x[0][0],ans.x[1][0]));
	}
}